ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Amandeep Singh1, Mandeep Kaur2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Reed Solomon codes are very efficient and can with stand the effect of various channel impairments such as
noise, interference and fading. The structure of simple LFSR type encoder is complex. Its complexity can be reduced by
reducing the complexity of GF(2m) field multipliers. Different methods of reducing complexity were studied in this paper.
Keywords |
| Reed Solomon, Galois Field, Generator Polynomial, LFSR. |
INTRODUCTION |
| Digital communication is immune to errors but still there persist some errors due to change in the bits. To overcome these errors error correcting codes are widely used in digital communication. Forward error correction is the one of the important part of digital communication systems. RS codes also corrects the unexpected error. RS codes were discovered by Irving S.Reed and Gustave Solomon, in Lincoln Laboratory of Massachusetts Institute of Technology in 1960. RS codes are based on arithmetic of finite fields and galois fields. The digital audio disk or compact disk uses Reed Solomon codes for error detection and error concealment. |
| RS encoding is based on addition operation and multiplication operation over Galois field (GF(2m)). Till now, many Finite field multiplier have been developed with low complexity such as parallel bases multipliers [1]. However, RS encoder still require use of many finite field multipliers and adders which results in large system complexity. For GF(2m) field m XOR gates will be required for the realization of addition operation and operation of multiplication requires m2 AND gates & m2-1 XOR gates using conventional approaches.[2] |
INTRODUCTION TO CODING |
| Reed Solomon codes are block codes and are represented as RS(n,k). where n is the size of output code and k is number of data symbols. n-k = 2t is the number of parity symbols. |
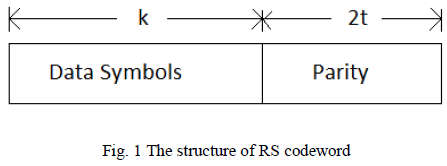 |
| Data block length: n |
| Number of message symbols: k |
| Number of parity symbols: n-k=2t |
| Each symbol at input is composed of m bits given by relation: |
| n = 2m – 1 (1) |
| The massage is divided into k symbols each of m bits long and 2t parity symbols are added to the m-bit k symbols to give n symbols of RS code. The information symbols are represented as a polynomial in powers of x from k-1 to 0 with most significance symbols having higher power. Reed Solomon codes are constructed using generator polynomial which is given by equation: |
| The code generated will be completely divisible by generator polynomial. The information symbols are first multiplied with Xn-k which will append n-k zeros to symbols & then divided by generator polynomial. The remainder will be retained and added to information symbols. Thus RS code is given by: |
| All the arithmetic calculation are done over Galois fields. All the symbols belong to Galois Field GF(2m). |
`REED SOLOMON ENCODER |
| RS encoder should be able to perform to operations namely division and shifting. Fig. 2 shows the block diagram of reed Solomon encoder it consist of shift registers labeled b0 through b2t-1. They are also called parity shift registers. Feedback data symbols are fed to the finite field multipliers labeled g0 through g2t-1 are the coefficient of generator polynomial. The working of Reed Solomon encoder can be explained as follow: |
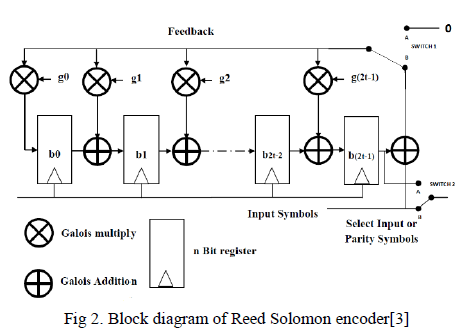 |
| 1. In initial stage each parity registers will contain a value zero. |
| 2. The message is divided into m-bit words. Each word is associated with increasing power of x forming message polynomial m(x). |
| 3. During the first k-clock pulses switches 1 and 2 are in position B. The output will be the message symbols. During these clock pluses LFSR will compute the remainder. |
| 4. When message symbols finished, switches are positioned to A. |
| 5. All the parity values are shifted out of the register one at a time. |
| The encoder defined in this section is a basic LFSR RS encoder. Many advancements have been done in past years, some of which are discussed as follow: |
| A. An efficient Reed Solomon encoder based on standard basis was presented by Sureridra K. Jairi et.al in 1996. The hardware complexity was same as Berelekamp encoder[4] but it was having advantages over it that were (a) critical path was having independence over of the order of reed Solomon code, (b) It can encode without any need of basis conversion .[5] |
| B. In 2004, J. jittawutipoka and J.Nagramnil proposed a new approach to implement RS encoder with low complexity. RS encoder was constructed with 15 multipliers only. The multipliers used were locally optimized but they also reduced the redundant operations. They implemented it with 124 XOR gates [2] which are much less then straightforward and locally optimized multipliers. |
| C. In 2005, G.C. Cardarilli et.al. Proposed a self-checking reed Solomon encoder. The self-checking property was analyzed using SEU fault model. The encoder was implemented on SRAM based FPGA. [6] |
| D. In 2012, Xiaojun Wu et.al Introduced the structure of RS encoder with improved algorithm of Galois field multiplier which saves the number of XOR gates. They proposed a design in which they further reduced the XOR gates used in Galois field multiplier with new proposed algorithm [7]. They compared their method of optimization with method given in [2] |
CONCLUSION |
| Reed Solomon codes are efficient and non-binary error correcting codes. Encoder is implemented using Linear Feedback Shift Register (LFSR). The irreducible generator polynomial is used to generate the code.RS codes have applications in the field where reliable and efficient data transfer is required in the presence of noisy enviorment. This paper briefly reviewed the reed Solomon encoder. Different methods were employed to reduce the complexity of encoder by reducing the finite field computations and multipliers. |
References |
|