ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| Vijayan T Asst professor, Dept of E&I, Bharath University, Chennai – 600073, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
BER is presented for the end to end performance of dual-hop wireless communication systems employing transmit diversity with orthogonal space-time block codes (OSTBCs), where a non regenerative or regenerative relay is equipped with a single antenna operating over flat Rayleigh fading channels. The end-to-end performance of dual-hop transmission certainly depends on the nature and complexity of relays. In nonregenerative systems, relays just amplify and forward the incoming signal without any other sort of manipulation on the signal. On the other hand, regenerative systems use more complicated relays that decode the signal received through the first hop and retransmit it, after encoding appropriately, into the second hop. More specifically, we provide probability density functions (PDF) and moment generating functions (MGF) for the end-to-end SNR of the dual-hop OSTBC transmissions and then present its BER performance over M-ary QAM and PSK modulations, respectively. Numerical investigation shows that the analytic BER provided in the paper makes an exact match with the simulation result in various multiple-antenna transmission scenarios. The result also shows how the number of antennas equipped at the source and destination affects the end-to-end performance
INTRODUCTION |
| The end-to-end performance of dual-hop transmission certainly depends on the nature and complexity of relays. Two main categories used in classifying the relays are, namely, nonregenerative and regenerative systems. In nonregenerative systems, relays just amplify and forward the incoming signal without any other sort of manipulation on the signal. On the other hand, regenerative systems use more complicated relays that decode the signal received through the first hop and retransmit it, after encoding appropriately, into the second hop. |
| Transmit diversity realized by multiple transmit antennas is widely accepted as an important tool for combating the fade in wireless links. It naturally affects the end-to- end performance when employed at any part in the dual-hop transmission. The existing performance studies of the dual- hop transmission, however, have focused on single-antenna transmission and the performance with multiple antennas is not well investigated so far. |
| In this project, considering a source and destination with multiple antennas as well as a single-antenna relay, we look into the end-to-end performance of dual-hop transmission with transmit diversity especially achieved by OSTBCs. We investigate both nonregenerative and regenerative systems and focus on the performance of bit error rate (BER). More specifically, we derive exact expressions for probability density functions (PDFs) and moment generating functions (MGFs) for the end-to-end signal-to-noise ratio (SNR) of the dual-hop OSTBC transmissions and then present its BER performance when M-ary QAM and M-ary PSK modulations are used, respectively. We assume the two hops experience independent, not necessarily identically distributed Rayleigh fadings but the multiple channels in each hop are mutually independent and identical. We also study the impact of the number of antennas equipped with the source and destination on the end-to-end BER performance. |
THE DUAL-HOP OSTBC SYSTEMS AND THE CHANNEL MODEL |
| We consider the dual-hop wireless communication system in which the source with nS t transmit (Tx) antennas is communicating with the destination with nD r receive (Rx) antennas through a single-antenna relay. (Hereafter, superscripts S, R and D denote the source, the relay and the destination, respectively.) It is assumed that the relay and the destination have perfect channel information for amplifying or decoding the respective signals received. We also assume that the communication between the source and the destination is unavailable. |
| In order to achieve spatial diversity, we assume that the source with multiple Tx antennas employs OSTBCs containing K complex symbols, x1, x2, · · ·, xK, to be transmitted. Especially, we consider the transmission matrices with the highest code rates for two, three and four Tx antennas. The OSTBC with nS t Tx antennas is denoted by Gn S t, where the number of columns is the block length and that of rows is the number of Tx antennas. The channel is assumed constant during the transmission block. |
| The 1×nS t channel vector for the first hop (i.e., received at the relay) and the nD r × 1 channel vector for the second hop (i.e., received by the destination) are respectively denoted by hR = {hR i }1×nStand hD = {hD i}nD r×1, where hR iand hD i represent the complex channel coefficients for the ith Tx and Rx antenna at the first and the second hop, respectively and are assumed an independent and identically distributed. complex Gaussian random variable (RV) with mean zero and variance β1/2 and β2/2 per dimension, respectively. |
A. SNR of Nonregenerative OSTBC Transmission |
| In the nonregenerative system considered in this letter, the relay simply amplifies and re-transmits the received signals into the second hop. When OSTBCs are used at the source, the signals received at the relay are given by |
 |
B.SNR of Regenerative OSTBC Transmission |
| In regenerative dual-hop OSTBC transmissions, the relay decodes the received signals with the squaring approach and transmits into the second hop. The signals received by the destination from the relay are expressed as YD = hDˆg+ED, |
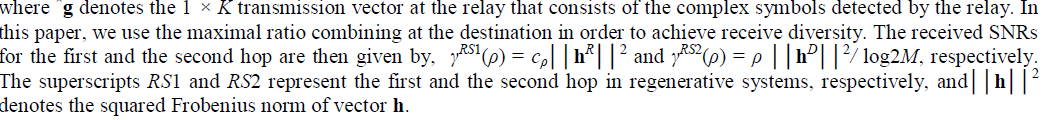 |
END-TO-END BER ANALYSIS |
A. BER Analysis in the Nonregenerative Systems |
 |
 |
 |
| Fig.1. Average BERs of nonregenerative and regenerative dual-hop OSTBCsystems when β1 = β2 = 1. |
| To obtain the MGF in (12). In the same way, the PDFs and the MGFs of γNS (ρ) for N = 3 and N = 4 can be obtained and their numerical results are also shown. Using the MGF and the PDF , we obtained the BER of M-ary QAM and M-ary PSK. |
B. BER Analysis in the Regenerative Systems |
| In regenerative systems, the signal received at the destination has undergone two states of decoding in cascade, and the end-to-end BERs of M-ary QAM and M-ary PSK constellations are respectively given by PU RS(ρ) = PU RS1(ρ) + PU RS2(ρ) − 2PU RS1(ρ)PU RS2(ρ), where U€{M − QAM,M − PSK}, subscript RS denotes the regenerative systems, and RS1 and RS2 represent the first and the second hop in the transmission, respectively. PU RS1(ρ)and PU RS2(ρ) denote the BERs of the respective constellations and hops. The BERs for M-ary QAM and PSK at each hop are obtained by using the equations of γRS1(ρ) and γRS2(ρ) in Section II.B, which have been derived for Rayleigh MIMO channels in Section III. |
NUMERICAL RESULTS |
| Dual-hop BERs for the nonregenerative and regenerative systems have been numerically evaluated and compared with simulation results. The BER curves are plotted for QPSK and 16-ary QAM. In Fig. 1, BERs are given for the nonregenerative and regenerative dual-hop MIMO transmission with OSTBCs for N = 2 and 4 when β1 = β2 = 1. Fig. 1 shows exact matches between the results from the analysis and the simulation. The figure also indicates that the BER performance improves as N increases. In comparing the nonregenerative systems with the regenerative systems, it is clear that regeneration of signals improves the BER performance at the cost of increasing relay’s complexity. However, it should be noted. |
 |
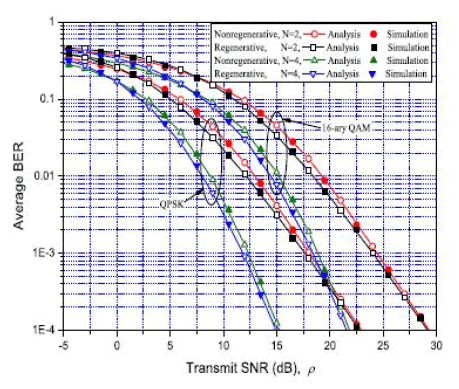
| Fig. 2. A comparison of dual-hop BERs with different amplifying gains, α* l and α, for nonregenerative OSTBC systems. |
 |
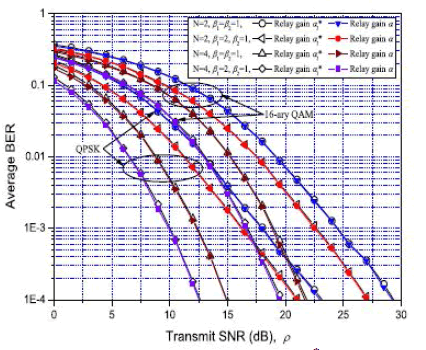
| Fig. 3. An impact of average received SNRs for the first and the second hop on the BER performances of nonregenerative and regenerative dual-hop OSTBC systems that nonregenerative systems can have the better BER when the transmit SNR is especially low. |
| Fig. 2 shows simulation results of dual-hop BERs in the nonregenerative systems with different amplifying gains, α* l and α, when β1 = β2 = 1 and β1 = 2, β2 = 1(β1 _= β2), respectively. It is clear from the figure that the BER for amplifying gain α is extremely tight lower bound on the BER for amplifying gain α* l even at low transmit SNR. A similar result was provided for SISO nonregenerative systems. |
| Let γ− 1 = ρβ1 and γ− 2 = ρβ2 denote the average received SNRs for the first and the second hop, respectively. Then Fig. 3 shows an impact of the average received SNRs for the first and the second hop on the BER performances of nonregenerative and regenerative dual-hop OSTBC systems. In Fig.3, it is observed that the BER performance degrades further from the optimal performance as the difference between the average received SNRs goes up (i.e., the intermediate relay is far from |
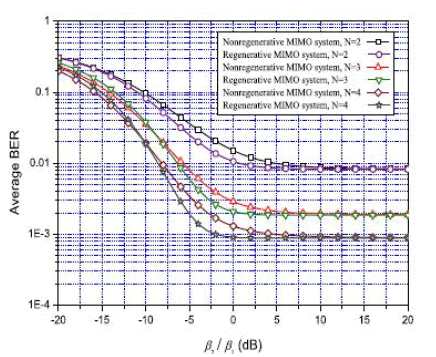 |
| Fig. 4. An impact of average channel gain ratio β2/β1 on the BER performances of nonregenerative and regenerative systems with QPSK when ρ = 12 dB and β1 = 1. |
| The middle between the source and the destination). For all the cases, the BER difference between nonregenerative and regenerative systems becomes small as the average received SNR for the first hop decreases (i.e., as the relay is close to the destination). For N = 4, it is remarked that the nonregenerative system performs better than the regenerative system when the average received SNR for the first hop is large (i.e., as the relay is close to the source). Using the BER results for the average received SNRs, optimal transmit powers can be allocated to the source and the relay. Fig. 4 shows an impact of the ratio of the average channel gain for the second hop to the first hop, β2/β1, on the BER performances of nonregenerative and regenerative systems with QPSK. We assume ρ = 12 dB and β1 = 1. As seen in Fig. 3, the BER gap between nonregenerative and regenerative systems becomes small at the both ends of the graphs for N = 2 but only at high ratios for N = 3 and 4. The gap is maximized between β2/β1 = −5 dB and −3 dB. when N = 3 and 4, the nonregenerative system achieves better BER performance than the regenerative system at low ratios where the average channel gain for the second hop is much smaller than that for the first hop. The reason is that, in the regenerative system, the second hop has the code rate of 1 regardless of the number of antennas N as in the equation of γRS2(ρ) and the end-toend performance is dominated by the second hop at the low ratio. |
CONCLUSIONS |
| This project has presented a study on the end-to-end performance of dual-hop wireless communication systems employing transmit diversity with OSTBCs, where a nonregenerative or regenerative relay is equipped with a single antenna. We have derived PDF and MGF of the dual-hop SNR. And then we can obtain BERs. Numerical results show that the BER analysis provided in the letter makes an exact match with the simulation in various multiple-antenna or relaying scenarios. |
References |
|