Temperature Studies in the Growth of Aspergillus Oryzae on Jowar Straw in Packed-Bed Solid State Fermenter (PBSSF) - A Modeling Approach

Abstract

Modeling of solid state fermenter (SSF) plays a vital role in understanding the bio process, design and development. Packed bed solid state fermenter (PBSSF) showed certain specified application over another types of SSF. Overall efficiency of this column majorly depends on the temperature gradients forms inside the column. Modeling is a good tool for the fermenter design. In this research work kinetic and lumped heat transport model were used for simulating the microbial growth in the PBSSF. In the present work, Aspergillus oryzae was grown on Jowar straw and then experimental findings were validated by checking satisfactory fit with the lumped model.

Keywords

Packed bed solid state fermenter (PBSSF), Kinetic and heat transfer model, Polymath, Aspergillus oryzae.

Introduction

Solid-state fermentation (SSF) involves the growth of microbes, mostly fungi [1] on water insoluble substrates in the absence of free water. SSF is very complex process where close process variable monitoring and controlling is required. Efficiency of SSF processes depends on interface between the three key components of the system: The bioreactor, the substrate and the micro-organisms [2,3] During the latest decade, SSF has experienced renewed interest due to many potential advantages of this bioprocess in comparison with submerged fermentation (SmF). These advantages include smaller bioreactor volumes, reduced downstream processing costs, superior productivity, simpler techniques, reduced energy requirements, low wastewater output [4]. Comparing with other types of SSF, PBSSF shows better process economics and even loading and unloading is easy in PBSSF. PBSSF is a cylindrical vessel with perforated base and hemispherical head. PBSSF is very easy for fabrication compared to another SSF’s, but process variables are very difficult to control. Larger bed heights are possible with PBSSF, in which air is forced through the bottom of the bed [5,7].In PBSSF oxygen supply is not limiting [8-9] Temperature variation formed inside the column is very severe technical problem with PBSSF. These temperature variations inside the column effect on the growth of micro-organism. The kinetic model shows the effect of these temperature variations on micro-organism growth. Heat generated inside the column will be dissipated by forced aeration which creates high temperature at the top of the column. Bathe et.al [10] showed that Jowar straw C:N ratio is above 18 and hence it is suitable substrate for SSF. In the current work temperature variations were studied for the growth of Aspergillus oryzae on jowar straw.

Experimental

The experimental setup of a PBSSF is shown in Figure 1. It consists of a cylindrical unit (1) with a capacity of 11.9 litres. It is 42 cm long vertical cylinder with internal diameter of 19 cm. The material used for the construction of fermentor system is SS-304. The base of fermentor is made up of wire mesh (2) with air distributor to facilitate aeration. The packed bed was aerated through air filter with a constant velocity of 70 m/hr. The bed temperatures were measured by thermocouple PT100 (3) placed at different axial positions and recorded by a data acquisition system (4).

Figure 1: SS-304 Packed-bed solid state fermenter (PBSSF): (1) Fermentation vessel, (2) Wire mesh with air distributor, (3) PT100 thermocouple, (4) Data acquisition system.

Materials and Method

Pretreatment of Raw Material

The measured quantity of Jowar straw was crushed in the mixer and screened to a mesh size of 36 for its utilization. The material was mixed with water and resulting thick slurry was pretreated in an autoclave for 0.5 hr at 1 bar. The mixture was gradually allowed to cooled down to ambient temperature and then dried in a convection oven to maintain overall moisture content in the range of 60% - 65%.

Inoculum Preparation

Spores of Aspergillus oryzae ware inoculated in Czapekdox broth having sucrose as the carbon source and incubated for 48 hours at 30°C. After incubation 5% v/w inoculums was inoculated in the pretreated substrate.

Material Properties

Bulk properties of the packed bed of substrate, like porosity, true density and bulk density were determined using pcynometer. Crushed jowar straw was pretreated with distilled water for 15 min and dried overnight. It was the filled in the pcynometer. The volume of toluene required to fill up all pores (spaces between two adjacent particles) was measured. Based on experiments, true and bulk properties were determined as follows.

Bed Porosity [11]

Bed porosity(ε) [12] of the substrate was calculated using following equation

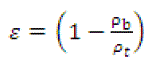..................(1)

Where,ρ_b is bulk density and ρ_t is true density of the bed.

Volume [13] was calculated by following relationship

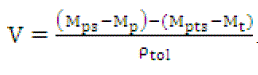.............(2)

Where M_t is mass of the pycnometer filled with toluene,M_ps is the mass of pycnometer and sample,M_p is the mass of the pycnometer,M_pts is the mass of the pynometer filled with toluene and the sample andρ_tol is the density of toluene. After calculating volume(V) , true density then can be calculated by following relation

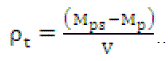......................(3)

Initial Biomass Calculation

Biomass was filtered from inoculum and washed thoroughly with de-ionized water and dried in tray dryer at 60oC for 48 hrs. Dried biomass was weighed at a regular interval of time (2hrs) for 48hrs. The constant weight value between 4 successive intervals was considered as final biomass concentration.

Mathematical model

In spite of mathematical simplicity with many unstructured models, they predict only adequate approximation of the whole growth curve in terms of three stages including the lag, exponential growth and stationary phases and exclude complete representation of the death phase [14].

In the present study, the growth kinetics of Aspergillus oryzae on Jowar straw in the batch bioreactor was correlated with temperature rate to predict behavior during lag, exponential growth stationary phases with an emphasize on death phase. The models describing interrelation of growth rate to the reactor temperature have already been devised as kinetic and transport models. The lumped model approach followed by Fanaei [14] has been used to investigate growth kinetics and heat transfer dynamics. Kinetic models describe how the microorganisms are influenced by various process parameters while transport model describes the mass and temperature profiles within the packed-bed bioreactor systems. In the current work Fanaei and Vaziri developed model is fitted for the experimental data generated when Aspergillus oryzae was grown on Sorghum bicolor (Jawari Straw)

Kinetic model

The parameter values used in the kinetic and lumped heat transfer model are given in Table 1 [14,15,17,19].Growth kinetics model for Aspergillus oryzae on Sorghum biocolour (Jawari Straw) are as follows:

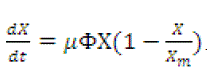...............(4)

Table 1: Parameter values used in the simulations with the mathematical model

Where, X, X_m Φ and are the biomass concentration, the maximum biomass concentration and the level of a physiological factor respectively. Physiological factor signifies the physiological state of the organisms during the course of fermentation and is function of temperature. Its value remains approximately equal to 1 during the biomass growth which indicates that is effect on growth in negligible in the temperature range selected.μ is the specific rate constant and calculated from equation (6).

Heat capacity of air (Cpa)

The heat capacity [15] of air (J kg-1oc-1) at 30 oC was calculated using correlation

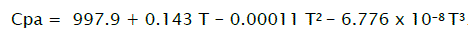.................(5)

Where, Cpa is heat capacity of air and T is inlet air temperature.

Specific growth rate constant[16] calculated by following relation

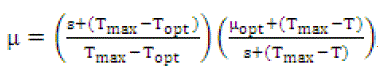.............(6)

Where, s is the sensitivity of the specific growth rate , Tmax and Topt are the maximum and optimum temperatures for micro-organism growth and μ_opt is the optimum specific growth rate constant.

Dynamic heat transfer models

Lumped dynamic heat transfer model expressed[14] as follows

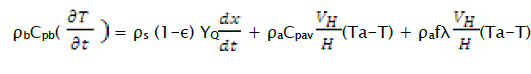..........(7)

Results and Discussion

In the present study it was assumed that the growth kinetics was carried out at the optimum water activity for growth and the effect of moisture content on growth is negligible. The experimental data used in this investigation were determined by lab experiments. The values of few parameters like porosity, substrate density, true density, initial biomass generated by experiments are given in Table 2.

Table 2:

The optimum temperature for the growth of Aspergillus oryzae is 30 oC. The experimental data is generated to fit the heat transfer models in a SSF process. The fermentor used in this work was a SS-304, packed bed column with 42cm height and 19 cm diameter. This fermenter was aerated from the bottom. Temperature variation profiles were reported at 25cm height and therefore, same height was used as a bioreactor height in the simulation. Fig 2 shows the predictions of lumped heat transfer model (temporal temperature profiles) with the experimental results. The results show that the predictions of lumped model are in good agreement with experimental data. The average of sum squared error (SSE) for predictions of lumped model is 4.67.

Figure 2: Comparison of the predictions of lumped heat transfer model with experimental data

Specific growth rate constant μ is a function of temperature. Growth rate of synthesis reaction and denaturation reaction was shown in fig.3 In PBSSF heat is majorly transferred by convective mode.Fig.4 indicate the biomass growth curve which shows the lag phase upto 20 hr then during the period 20 hr to 45 hr exponential phase was observed and above 45 hr to 65 hr stationary phase was observed. After 45 hr growth curve slope decreases because at this time temperature rich to high reading affect spore germination and growth. Hence after 45 hr temperature was observed to be almost constant up to 65 hrs indicate stationary phase as shown in fig.2. As after 65 hrs the temperature was observed to be decreased due to high spore germination and decreases the growth rate which indicate death phase.

Figure 3: Specific growth rate vs bed temperature

Figure 4: Growth of Aspergillus oryzae on Jawar straw.

According to Mitchell DA et.al [20,21] temperature gradients forms in PBSSF are impossible to avoid and sometimes these gradient may be steep due to the end to end aeration. Between the time 20 to 45 hr the temperature gradients were steep. These results shows that between this time period metabolic activities of the micro-organism were very high which generates heat. Numerical solution of the kinetic and heat transfer models were performed by the STIFFBS method in Polymath 6.1- educational version, with the regression coefficient (r2) of 0.997. This value of r2 shows that the lumped model was effectively fitted to experimental data. To verify the validity of kinetic model proposed by Fanaei and Vaziri, experimental data generated for the growth of Aspergillus oryzae on jowar straw was used. The results are shown in Fig.4. From the results, the model predictions agreed reasonably well with the experimental data.

Conclusion

In the present study, the growth kinetics of Aspergillus oryzae on Jowar straw in the batch bioreactor was correlated efficiently with temperature rate to predict behavior during lag, exponential growth stationary phases with an emphasize on death phase. Kinetic and lumped heat transfer models were tested for PBSSF. Experimental data of temperature variation was fitted properly using this model. This model used the novel approach of the influence current temperatures on growth phases. An attempt is made to completely represent the death phase using relationship between specific rate constant and temperature.

Acknowledgements

The author would like to thank to the University Grants Commission (UGC), India for financially supporting the research project entitled “Temperature gradient studies in packed bed solid state fermenter”.

Appendix A. Nomenclature

Cpa Heat capacity of air ( J/kg oc)

Cps Heat capacity of substrate ( J/kg oc)

f Water carrying capacity of air (kg-water/kg-air oc)

H Bed height (m)

Ka Thermal conductivity of moist air (J/hr m oc)

Ks Thermal conductivity of substrate (J/hr m oc)

t Time (hr)

T Bed temperature (oc)

To Initial bed temperature (oc)

Ta Inlet air temperature (oc)

Tmax Maximum Temperature for growth (oc)

Topt Optimum temperature for growth (oc)

V_H Velocity of moist air (m/hr)

X Biomass concentration (kg-biomass/kg-substrate)

X₀ Initial biomass concentration (kg-biomass/ kg-substrate)

X_m Maximum biomass concentration (kg-biomass/ kg-substrate)

YQ Metabolic heat yield coefficient (J/kg-biomass)

H Axial position

H Bed height (m)\

Greek letters

ε Porosity

λ Latent evaporation of water (J/Kg)

μ Specific growth rate constant (hr^-1)

μ_opt Optimum specific growth rate constant (hr^-1)

ρ_a Moist air density (kg/m³)

ρ_s Substrate density (kg/m³)

Ρ_t True density (kg/m³)

References

1. Pandey A, Soccoll CR, Mitchell DA. New developments in solid-statefermentation: I––Bioprocesses and products. ProcBiochem 2000; 35:1153–1169.
2. Sangsurasak P, Mitchell DA. The investigation of transient multidimensional heat transfer in solid-state fermentation. Chem Engineering J. 1995;60:199-204.
3. PenijitSrinophakun, ThongchaiSrinophakhun. Bioreactor performance and design of large scale packed bed solid state fermentation. J NatSci. 1998;32:333-338.
4. Mudgen RE. Solid state fermentations, in Manual of industrial Microbiology and Biotechnology Process (Demain, A. L. and Solomon, M. A., eds.). American Society for Microbiologists, Washington, DC, 1986; 66-83.
5. M Khanahmadi, R Roostaazad, DA Mitchell, M Miranzadeh, R Bozorgmehri, et al. Bed moisture estimation by monitoring of air stream temperature rise in packed bed solid state fermentation, ChemEng Sci.61(2006)5354-5363.
6. Robinson T, Nigam P. Bioreactor design for protein enrichment of agricultural residues by solid state fermentation. BiochemEng J.2003;13:197-203.
7. Ghildyal NP, Gowthaman MK, Raghava Rao KSMS, Karanth NG. Interaction between transport resistances with biochemical reaction in packed bed solid state fermenters:effect of temperature gradients. Enzyme MicrobTechnol.1994;16:253-257.
8. Saucedo-Castaneda G, Lonsane BK, Krishnath MM. Navarro JM, Roussos S, Raimbault M. Maintenance of heat and water balances as a scale-up criterion for the production of ethanol by Schwanniomycescastelli in a solid state fermentation system. ProcBiochem 1992;27:97-107.
9. Gowthaman MK, Ghildyal NP, Raghava Rao KSMS, Karanth NG. Interaction of transport resistances with biochemical reaction in packed bed solid state fermenters:The effect of gaseous concentration gradients. J ChemTechnolBiotechnol. 1993;56:233-239.
10. Bathe GA, Patil VS, Chaurasia AS. Study on temperature gradients and protein enrichment by Aspergillusoryzae in solid state fermentation on packed bed bioreactor using jowar (sorghum) straw as substrate. J Sustainable Bioenergy System. 2012;2:33-36.
11. KhusalBrijwani, Praveen V Valdlani. Cellulolytic enzymes production via solid-state fermentation: effect of pretreatment methods on physicochemical characteristics of substrate. Enzyme Res. 2011;1-10.
12. Abalone R, cassinera A, Gastone A, Lara MA. Some physical properties of amaranth seeds. Biosystems Eng. 2004;89:109-117.
13. Milani E, Seyed M, Razavi A. et al. Moisture dependent physical properties of cucurbit seeds. IntAgrophys. 2007;21(2):157-168.
14. Mohammad Ali Fanaei, BehroozMahmoodzadehVaziri. Modeling of temperature gradients in packed bed solid state bioreactors. ChemEng Proc. 2009;48:446-451.
15. Himmelblau DM. Basic Principles and Calculations in Chemical Engineering,5thed.,Prentice Hall, Englewood Cliffs.1982.
16. Sweat VE. Thermal Properties of Foods, in:Rao MA, Rizvi SS(Eds.)Engineering properties of foods, Marcel Dekker, New York. 1986;49-132
17. Perry RH, Green DW, Maloney JO. Perry’s Chemical Engineer’s Handbook, 6th ed. McGraw Hill Publication, New York.1984.
18. Sangsurasak P, Mitchell DA. Validation of a model describing 2-dimensional heat transfer during solid state fermentation in packed bed bioreactors. Biotechnol Bioeng.1998;60:739-749.
19. Saucedo-Casteneda G, Gutierre-Rojas M, Bacquet G, Raimbault M, Viniegra-Gonzalex G. Heat transfer simulation in solid substrate fermentation. Biotechnol Bioeng.1990; 35:802-808.
20. Mitchell DA, Von Meien OF, Krieger N, Recent developments in modeling of solid-state fermentation: heat and mass transfer in bioreactors. BiochemEng J.2003;13:137-147.
21. Mitchell DA. Krieger N, Stuart DM, Pandey A. New developments in solid state fermentation II, Rational approaches to the design,operation and scale up of bioreactors. Process Biochem. 2000;35:1211-1225.