ISSN: 2320-0189
ISSN: 2320-0189
1Department of Electronics and Telecommunication Engg, BMIT, Solapur, Maharashtra, India
2Department of Physics, BMIT, Solpur, Maharashtra, India
Received date: 11 May 2014 Accepted date: 13 June 2014
Visit for more related articles at Research & Reviews: Journal of Botanical Sciences
By observing leaf, we can easily identify plant but it is difficult to identify its species. In this project we developed an algorithm that gives user the ability to identify plant species based on photographs of the leaf. The core theme of this application is an algorithm that acquires statistical features of the leaves, and then classifies the species based on a novel combination of the computed texture feature analysis and wavelet analysis. While implementing this algorithm we have considered the Grape plant and its four species viz. Clone, Sonaka, Thomson and Manik. The algorithm is first trained against several samples of known plant species and then used to classify unknown query species. By using this algorithm we have achieved 93.33% efficiency.
Grape plant, Clone, Sonaka, Thomson and Manik
This Convergence of multidisciplinary research is more and more considered as the next big thing to answer profound challenges of humanity related to health, biodiversity or sustainable energy. The integration of life sciences and computer sciences has a major role to play towards managing and analyzing cross-disciplinary scientific data at a global scale. More specifically, building accurate knowledge of the identity, geographic distribution and uses of plants is essential if agricultural development is to be successful and biodiversity is to be conserved. Unfortunately, such basic information is often only partially available for professional stakeholders, teachers, scientists and citizens, and often incomplete for ecosystems that possess the highest plant diversity. A noticeable consequence, expressed as the taxonomic gap, is that identifying plant species is usually impossible for the general public, and often a difficult task for professionals, such as farmers or wood exploiters and even for the botanists themselves. The only way to overcome this problem is to speed up the collection and integration of raw observation data, while simultaneously providing to potential users an easy and efficient access to this botanical knowledge. In this context, content-based visual identification of plant's images is considered as one of the most promising solution to help bridging the taxonomic gap [1,2,3].
In the field of comparative biology, novel sources of data are continuously being sought to enable or enhance research varying from studies of evolution to generating tools for taxon identification. Leaves are especially important in this regard, because in many applied fields, such as studies of ecology or paleontology, reproductive organs, which may often provide an easier form of identification, are unavailable or present for only a limited season. Leaves are present during all seasons when plants are in growth. There are also millions of dried specimens available in herbaria around the world, many of which have already been imaged. While these specimens may possess reproductive organs, the main character features are often concealed in images through being internal or due to poor preparation. However, almost all specimens possess well-preserved and relatively easily imaged leaf material [4].
In this I developed an algorithm that gives user the ability to identify plant species based on photographs of the plant’s leaf taken by a camera. At the heart of this application is an algorithm that acquires statistical features of the leaves, and then classifies the species based on a novel combination of the computed texture and colour analysis. The first algorithm is trained against several samples of known plant species and then used to classify unknown query species. The algorithm is very successful in properly classifying species contained in the training library.
It may be relatively easy to tell the name of plant from its leaf but identifying the exact species can be extremely difficult by only observing its leaf. In many cases it may even be necessary to collect samples and consult an expert to make an accurate identification. Nevertheless, it is possible to identify certain species of plants quite easily, by simply examining a few of their characteristics. So in order to make this easy there is a need of an algorithm which will help a common person to easily identify a plant species without consulting the experts [5].
Related Work
Yanhua Ye, et al. [5] proposed a computerized plant species recognition system (CPSRS). CPSRS is a Web-based application that ensures an efficient way to search and identify field plant species. It is built on a Java Web infrastructure to support platform-independent application. Java applets and servlets are adopted to balance the burden of computing in the client and server. The CPSRS architecture introduced and shows its design and working. Two types of plant species retrieval methods, text-based information retrieval and content-based leaf retrieval are discussed. With the former, exact plant species information is retrieved from the database according to input searching criteria provided. For content based leaf retrieval, experiments reveal a recall rate of about 71.4% when top five returned images are considered.
Fu, et al., [6] proposed an ontology-based leaf classification system, where machine learning techniques are used for automatic classification. Leaf classification, indexing and retrieval are an integral part of a computerized plant identification system. The leaf contour classification used a scaled CCD code to categorize the shape and margin type of a leaf by using a principle usually adopted by botanists. Then a trained neural network is employed to recognize detailed tooth patterns. An unlobed leaf is also measured according to methods employed by botanists. For leaf vein recognition, the vein texture is extracted through a combined thresholding and neural network approach so that more leaf details are made available. Compared to past studies, the proposed method integrates low-level image features and specific domain knowledge (ontology) of botany, and thus ensures a user friendly system. Primary experiments showed promising results, proving the system’s feasibility.
Wang, et al., [7] proposed a classification framework for leaf images with complicated backgrounds. Classification of plant leaves had always been difficult as their complicated backgrounds included interference and overlapping phenomena. An automatic marker-controlled watershed segmentation method along with pre-segmentation and morphological operations was introduced to segment leaf images which had complicated backgrounds. Based on earlier shape information, seven Hu geometric moments and sixteen Zernike moments were extracted as shape features from the segmented binary images after leafstalk removal. In addition, a moving center hyper-sphere (MCH) classifier capable of compressing feature data was designed to handle mass high dimensional shape features. In the end the study results on practical plant leaves revealed that the proposed classification framework worked well in classifying leaf images having complicated backgrounds. A total of 20 practical plant leaves were successfully classified with correct classification averaging 92.6%.
Ji-Xiang Du, et al., [8] proposed computer-aided plant species identification (CAPSI) approach using a shape matching technique. A modified dynamic programming (MDP) algorithm for shape matching was used for plant leaf recognition and the study revealed that it trotted up a high accuracy rate of over 92 % as it was better than others in the recognition of blurred leaf images. When it came to classification of partial leaves, the MDP algorithm used proved to be more efficient in comparison to other methods. Similarly for retrieval of leaves this procedure was far better than those of competitors. The superiority of the proposed method over traditional approaches to plant species identification was demonstrated by experiments which showed that the algorithm used was suitable for the recognition of not only intact but also partial, distorted and overlapped plant leaves due to its robustness.
Rashad, et al., [9] introduced an approach to plant classification based on characterization of texture properties. A combined classifier learning vector quantization was utilized. The advantage of the proposed system was its ability to classify and recognize a plant from a small part of the leaf without needing to depend either on the shape of the full .
Leaf or its color features. This was due to the fact that the system essentially depended on the part’s textural features. Hence, the system can be used by researchers of Botany who need to identify damaged plants, as it can now be done from a small available part. Similarly when researchers need to classify a plant and have only a portion available that is in itself enough to do the needful as the proposed system textural features are required and not color features which are liable to change with the changing season. The results revealed that the combined classifier method produced high performance far superior to other tested methods as its correct recognition rate was 98.7% and hence applicable. In this paper, it is proposed to extract features using the Sobel edge detection and Gabor filters. The features are fused to create the dataset. The proposed feature extraction method is tested against Classification and Regression Tree (CART) classifier and Radial Basis Function (RBF) classifier.
Basic Theory
The Discrete Wavelet Transforms (DWT)
Is a mathematical tool for hierarchically decomposing an image. It is useful for processing of non-stationary signals. The transform is based on small waves, called wavelets, of varying frequency and limited duration. Wavelet transform provides both frequency and spatial description of an image. Unlike conventional Fourier transform, temporal information is retained in this transformation process. Wavelets are created by translations and dilations of a fixed function called mother wavelet.DWT is the multi resolution description of an image the decoding can be processed sequentially from a low resolution to the higher resolution. The DWT splits the image into high and low frequency parts. The high frequency part contains information about the edge components, while the low frequency part is split again into high and low frequency parts. The high frequency components are usually used for watermarking since the human eye is less sensitive to changes in edges.
In two dimensional applications, for each level of decomposition, we first perform the DWT in the vertical direction, followed by the DWT in the horizontal direction. After the first level of decomposition, there are 4 sub-bands: LL1, LH1, HL1, and HH1. For each successive level of decomposition, the LL sub band of the previous level is used as the input. To perform second level decomposition, the DWT is applied to LL1 band which decomposes the LL1 band into the four sub to perform third level decomposition, the DWT is applied to LL2 band which decompose this band into the four sub-bands – LL3, LH3, HL3, HH3. These results in 10 sub-bands per component. LH1, HL1, and HH1 contain the highest frequency bands present in the image tile, while LL3 contains the lowest frequency band. The three-level DWT decomposition is shown in Fig (1).
DWT is currently used in a wide variety of signal processing applications, such as in audio and video compression, removal of noise in audio, and the simulation of wireless antenna distribution. Wavelets have their energy concentrated in time and are well suited for the analysis of transient, time-varying signals.
Since, most of the real life signals encountered are time varying in nature, the Wavelet Transform suits many applications very well
Before the stage of features extraction, the image are processed by a silence removing algorithm followed by the application of a pre-processed by applying the normalization on images to make the image comparable regardless of differences in magnitude.
Efficiently supported wavelets are generally used in various applications. In the last decade, there has been a huge increase in the applications of wavelets in various scientific disciplines. Typical applications of wavelets include signal processing, image processing, security systems, numerical analysis, statistics, biomedicine, etc. Wavelet transform tenders a wide variety of useful features, on the contrary to other transforms, such as Fourier transform or cosine transform. Some of these are as follows:
• Adaptive time-frequency windows,
• Lower aliasing distortion for signal processing applications,
• Computational complexity of O (N), where N is the length of data;
• Inherent scalability;
• Efficient Very Low Scale Integration implementation
[10] In two dimensions, a two dimensional scaling function, φ (x,y) and three two dimensional wavelets ΨH(x,y), ΨV(x,y) and ΨD(x,y) are required. Each is the product of one dimensional scaling function φ and corresponding wavelet Ψ. Excluding products that produce one dimensional results, like φ(x) Ψ(x), the four remaining products produce the separable scaling function
φ (x,y) = φ(x) . φ(y) ---------------(i)
and separable “directionally sensitive” wavelets
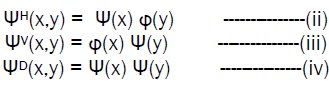
These wavelets measure functional variations – intensity or gray level variations for images –along different directions: ΨH measures variations along columns, ΨV responds to variations along rows and ΨD corresponds to variations along diagonals. The directional sensitivity is a natural consequence of the separability imposed by equation (ii) to (iv); it does not increase the computational complexity of the two dimensional transform.
Given separable two dimensional scaling and wavelet functions, extension of the one-dimensional DWT to two-dimensional is straightforward. We first define the two dimensional scaled and translated basis function:
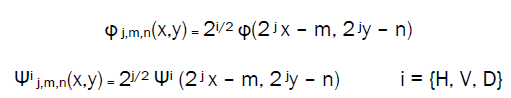
Where index I identify the directional wavelets in eqn (ii) to (iv). Rather than an exponent, I is a subscript that assumes the values H, V and D. The discrete wavelet transform of a function
Neural Network
Neural networks are composed of simple elements operating in parallel. These elements are inspired by biological nervous systems. As in nature, the network function is determined largely by the connections between elements. We can train a neural network to perform a particular function by adjusting the values of the connections (weights) between elements. Commonly neural networks are adjusted, or trained, so that a particular input leads to a specific target output. Such a situation is shown below. There, the network is adjusted, based on a comparison of the output and the target, until the network output matches the target. Typically many such input/target pairs are used, in this supervised learning, to train a network.
Batch training of a network proceeds by making weight and bias changes based on an entire set (batch) of input vectors. Incremental training changes the weights and biases of a network as needed after representation of each individual input vector. Incremental training is sometimes referred to as “on line” or “adaptive” training. Neural networks have been trained to perform complex functions in various fields of application including pattern recognition, identification, classification, speech, and vision and control systems. Today neural networks can be trained to solve problems that are difficult for conventional computers or human beings. Throughout the toolbox emphasis is placed on neural network paradigms that build up to or are themselves used in engineering, financial and other practical applications.
Neural Network including connections (called weights) Input between neurons Output Target Adjust weights Compare Neural Networks. The supervised training methods are commonly used, but other networks can be obtained from unsupervised training techniques or from direct design methods. unsupervised networks can be used, for instance, to identify groups of data. Certain kinds of linear networks and Hopfield networks are designed directly. In summary, there are a variety of kinds of design and learning techniques that enrich the choices that a user can make. The field of neural networks has a history of some five decades but has found solid application only in the past fifteen years, and the field is still developing rapidly. Thus, it is distinctly different from the fields of control systems or optimization where the terminology, basic mathematics, and design procedures have been firmly established and applied for many years. We do not view the Neural Network Toolbox as simply a summary of established procedures that are known to work well. Rather, we hope that it will be a useful tool for industry, education and research, a tool that will help users find what works and what doesn’t, and a tool that will help develop and extend the field of neural networks
Because the field and the material are so new, this toolbox will explain the procedures, tell how to apply them, and illustrate their successes and failures with examples. We believe that an understanding of the paradigms and their application is essential to the satisfactory and successful use of this toolbox, and that without such understanding user complaints and inquiries would bury us. So please be patient if we include a lot of explanatory material. We hope that such material will be helpful to you [11].
The performance of classifier is defined by the feature used to train the network.So as in our case DWT provides strong feture vector depending on those conditions the results for the experiments are given in tables 1 and 2. For the two leaf datasets, all the algorithms performed better on the dataset created as described in section 2, showing the value of our method of leaf texture extraction.
This paper addresses how the identification of plant species is possible for the grape plant by effectively analysing the various parameters of leaf by using DWT and neural network. The experimental results indicate that the proposed approach is a valuable approach, which can significantly support an accurate detection of plant species in a little computational effort. Trees can often show different appearances in different seasons and even the same tree species may vary due to their health status. Nevertheless, from our experiment we can conclude that there can be much difference in different plant leafs but there is not much difference in species of same plant. The feature extraction algorithm was computationally efficient and can meet real-time application requirements. Therefore, this system can be concluded as a promising technique for plant species classification.
Future Scope
The research can be improved by gathering a larger training set using other leaf shapes. We can explore more algorithms and techniques for the feature extraction and classification of biological species to further improve the accuracy of the identification system. We can further improve the system by reducing the complexity. The main objective could be to find the best algorithms which optimize the performance and complexity. The accuracy of classifier can also be enhanced by using more and equal number of training patterns.