ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
H. R. Eghtesad Doost1, M. C. Amirani2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In this paper, a new algorithm which is based on the continues wavelet transformation and local binary patterns (LBP) for content based texture image classification is proposed. We improve the Local Binary Pattern approach with Wavelet Transformation to propose the texture classification. We used 12 classes of Brodatz textures data base for proposed method. Each class is divided to 64 texture image and then wavelet transformation is applied to each texture. After transformed texture from wavelet the feature extraction matrix is formation using LBP. The same concept is utilized at LBP calculation which is generating nine LBP patterns from a given 3×3 pattern. Finally, nine LBP histograms are calculated which are used as a feature vector for image classification. Two experiments have been carried out for proving the worth of our algorithm. It is further mentioned that the database considered for experiments are Brodatz database. We verify the other method and proposed method is very good and efficient for classification texture image.
Keywords |
| Texture Classification, Local Binary Pattern, Wavelet Transformation. |
INTRODUCTION |
| Texture classification is a fundamental issue in computer vision and image processing, playing a significant role in a wide range of applications that includes medical image analysis, remote sensing, object recognition, document analysis, environment modeling, content-based image retrieval and many more [3]. The local binary pattern (LBP) is one of the most used texture descriptors in image analysis. In this paper, we extend the original LBP with continues wavelet transformation for texture analysis and classification. The proposed method presents the comparative results of classification using both feature sets separately and in combination. The paper is organized as follows. In the next section, a brief introduction for demonstrating basic concepts of Local Binary Pattern (LBP) is given. In the section 3 Continues Wavelet Transformation is introduced. In the Section 4 the Feature extraction and proposed method is described and in the section 5 experimental results of this method are given. The conclusion of this paper is given in section 6. |
LOCAL BINARY PATTERN |
| The original LBP operator, introduced by Ojala et al. [19], is a powerful means of texture description. The operator labels the pixels of an image by thresholding the 3x3-neighbourhood of each pixel with the center value and converts the result into a binary number by using (1). |
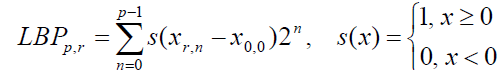 |
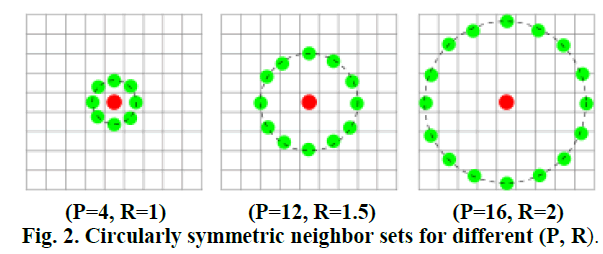
| Two extensions of the original operator were made in [2]. The first defined LBPs for neighborhoods of different sizes, thus making it possible to handle textures at different scales. Using circular neighborhoods and bilinear interpolating the pixel values allow any radius and number of pixels in the neighborhood. In this extension, P sampling points on a circle of radius of R, are shown to form a (P, R). The second defined the so-called uniform patterns: an LBP is uniform if it contains at most one 0-1 and one 1-0 transition when viewed as a circular bit string. For example, 00000000, 00011110 and 10000011 are uniform patterns. Uniformity is important because it characterizes the Pieces that include primitive structural information such as edges and corners. Ojala et al. noticed that in their experiments with texture images, uniform patterns account for a bit less than 90% of all patterns when using the (8,1) neighborhood and for around 70% in the (16,2) neighborhood. There are various extensions and reformations of the original LBP following its first introduction by Ojala et al [1]. Figure 2 shows some examples of the circularly symmetric neighborhoods. |
 |
| The gray values of neighbors which do not lie precisely in a pixel location may be estimated by interpolation. Given an N_M image I, let LBPp,r(i,j) be the identified LBP pattern of each pixel (i, j), then the whole texture image is represented by a histogram vector h of length K: |
 |
| The LBP feature vector, in its simplest form, is created in the following manner: |
| Divide the examined window into cells (e.g. 16x16 pixels for each cell). |
| For each pixel in a cell, compare the pixel to each of its 8 neighbors (on its left-top, left-middle, left-bottom, right-top, etc.). Follow the pixels along a circle, i.e. clockwise or counter-clockwise. |
| Where the center pixel's value is greater than the neighbor's value, write "1". Otherwise, write "0". This gives an 8-digit binary number (which is usually converted to decimal for convenience). |
| Compute the histogram, over the cell, of the frequency of each "number" occurring (i.e., each combination of which pixels are smaller and which are greater than the center). |
| Optionally normalize the histogram. |
| Concatenate (normalized) histograms of all cells. This gives the feature vector for the window. |
| The feature vector can now be processed using the support vector machine or some other machine-learning algorithm to classify images. Such classifiers can be used for face recognition or texture analysis. The 12 texture classes from the Brodatz album [9] is shown in Figure 3 actually are misclassified by using only the conventional LBP or according to our experimental results. |
 |
| In the above 12 textures, they all have the same sets of dominant patterns with very similar proportions, and the pattern type labelled with 24 is one of the dominant patterns. As we can see, the numbers of such dominant patterns in each texture are very close to each other. However, the distribution properties of this pattern in these 12 texture images are very different with each other. Therefore, the Continuous Wavelet Transformation is a very important property to describe the textures, which will be further illustrated in the Experimental Results section. |
CONTINUOUS WAVELET TRANSFORMATION |
| A continuous wavelet transform (CWT) is used to divide a continuous-time function into wavelets. Unlike Fourier transform, the continuous wavelet transform possesses the ability to construct a time-frequency representation of a signal that offers very good time and frequency localization. In mathematics, the continuous wavelet transform of a continuous, square-integrable function x(t) at a scale a ≥0 and translational value b R is expressed by the following integral |
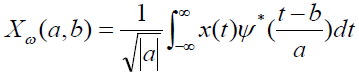 |
| where (t) is a continuous function in both the time domain and the frequency domain called the mother wavelet and * represents operation of complex conjugate. The main purpose of the mother wavelet is to provide a source function to generate the daughter wavelets which are simply the translated and scaled versions of the mother wavelet. To recover the original signal x(t) , inverse continuous wavelet transform can be exploited. |
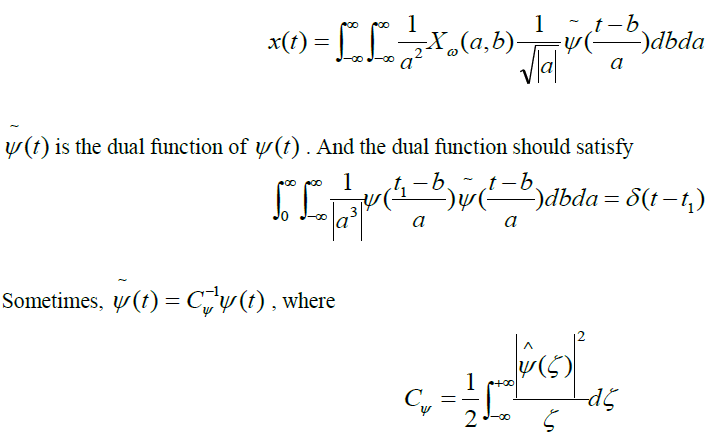 |
 |
| Mother wavelet: In general, it is preferable to choose a mother wavelet that is continuously differentiable with compactly supported scaling function and high vanishing moments. A wavelet associated with a multiresolution analysis is defined by the following two functions: the wavelet function (t) , and the scaling function(t) . The scaling function is compactly supported if and only if the scaling filter h has a finite support, and their supports are the same. For instance, if the support of the scaling function is [N1, N2], then the wavelet is [(N1-N2+1)/2,(N2-N1+1)/2]. On the other hand, the kth moments can be expressed by the following equation conditions of mother wavelet 1) admisibility 2) regularity 3) no of vanishing moments |
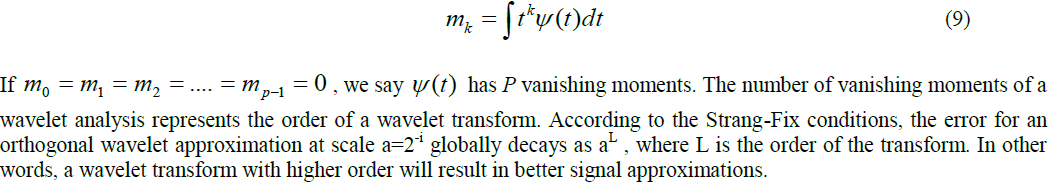 |
| Scaling function: The wavelet function (t) and the scaling function (t) define a wavelet. The scaling function is primarily responsible for improving the coverage of the wavelet spectrum. This could be difficult since time is inversely proportional to frequency. In other words, if we want to double the spectrum coverage of the wavelet in the time domain, we would have to sacrifice half of the bandwidth in the frequency domain. Instead of covering all the spectrum with an infinite number of levels, we use a finite combination of the scaling function to cover the spectrum. As a result, the number of wavelets required to cover the entire spectrum has been greatly reduced. |
| Scale factor: The scale factor either dilates or compresses a signal. When the scale factor is relatively low, the signal is more contracted which in turn results in a more detailed resulting graph. However, the drawback is that low scale factor does not last for the entire duration of the signal. On the other hand, when the scale factor is high, the signal is stretched out which means that the resulting graph will be presented in less detail. Nevertheless, it usually lasts the entire duration of the signal. |
| Continuous wavelet transform properties: In definition, the continuous wavelet transform is a convolution of the input data sequence with a set of functions generated by the mother wavelet. The convolution can be computed by using the Fast Fourier Transform (FFT). Normally, the output X (a,b) is a real valued function except when the mother wavelet is complex. A complex mother wavelet will convert the continuous wavelet transform to a complex valued function. The power spectrum of the continuous wavelet transform can be represented by 2 X (a,b) . |
| Applications of the wavelet transform: One of the most popular applications of wavelet transform is image compression. The advantage of using wavelet-based coding in image compression is that it provides significant improvements in picture quality at higher compression ratios over conventional techniques. Since wavelet transform has the ability to decompose complex information and patterns into elementary forms, it is commonly used in acoustics processing and pattern recognition. Moreover, wavelet transforms can be applied to the following scientific research areas: edge and corner detection, partial differential equation solving, transient detection, filter design, electrocardiogram (ECG) analysis, texture analysis, business information analysis and gait analysis. |
| Continuous Wavelet Transform (CWT) is very efficient in determining the damping ratio of oscillating signals (e.g. identification of damping in dynamical systems). CWT is also very resistant to the noise in the signal. |
FEATURE EXTRACTION |
| The feature selection process usually is designed to provide a means for choosing the features which are best for classification optimized against on various criteria. The feature selection process performed on a set of predetermined features. Features are selected based on either (1) best representation of a given class of texture, or (2) best distinction between classes. Therefore, feature selection plays an important role in classifying systems such as neural networks. For the purpose of classification problems, the classifying system has usually been implemented with rules using if then clauses, which state the conditions of certain attributes and resulting rules. However, it has proven to be a difficult and time consuming method. From the viewpoint of managing large quantities of data, it would still be most useful if irrelevant or redundant attributes could be segregated from relevant and important ones, although the exact governing rules may not be known. In this case, the process of extracting useful information from a large data set can be greatly facilitated [8–10]. In the feature extraction stage, numerous different methods can be used so that several diverse features can be extracted from the same raw data. The wavelet transform (WT) provides very general techniques which can be applied to many tasks in image processing. Wavelets are ideally suited for the analysis of sudden short-duration image changes. |
EXPERIMENTAL RESULT |
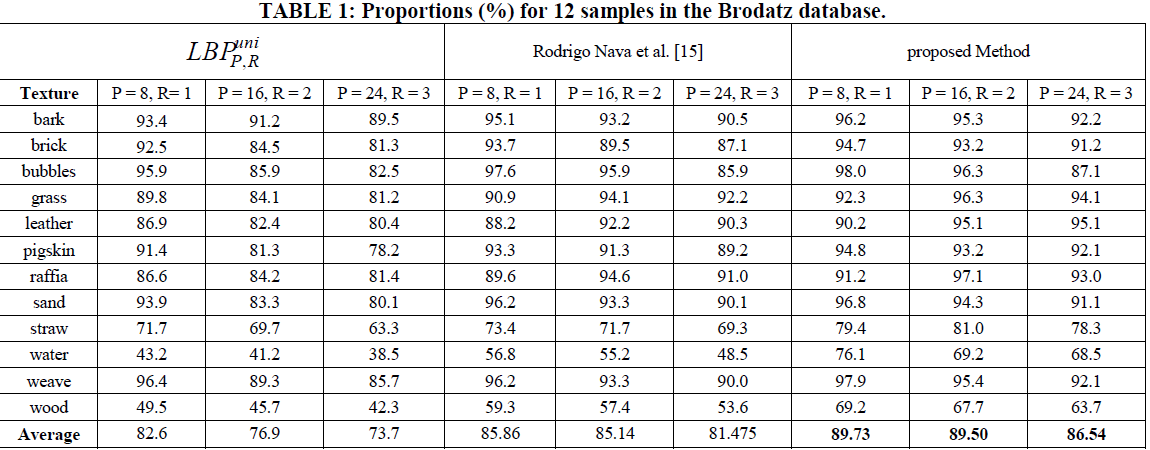
| According to the experimental results, the proposed LBP approach can already outperform the other method under different conditions. Also, by embedding the wavelet transformation information of dominant patterns with the LBP, the classification performance is better than using LBP alone. |
 |
CONCLUSION |
| In this paper, we offered novel Local Binary Pattern (LBP) operator to deal with main defect of the original LBP operator based on wavelet transformation. It has been evaluated by comparing with several methods with Brodatz databases. It is experimentally shown that our approach has excellent performance in texture classification and is very robust to histogram equalization and random rotation. Computational simplicity is another advantage of our proposed method as the features can be obtained with only a few calculations and comparisons without the need of performing any image filtering. |
References |
|