THE COMPARATIVE ANALYSIS OF A
FUZZY TRANSFORM BASED IMAGE
COMPRESSION TECHNIQUE WITH THE
OTHER METHODS

Neha Gupta; Prof. Mahesh Prasad Parsai

THE COMPARATIVE ANALYSIS OF A FUZZY TRANSFORM BASED IMAGE COMPRESSION TECHNIQUE WITH THE OTHER METHODS

Neha Gupta, Prof. Mahesh Prasad Parsai

Student, Department of ECE, JEC Jabalpur, Madhya Pradesh, India
Professor, Department of ECE, JEC Jabalpur, Madhya Pradesh, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

This article presents a comparative analysis of various method of image compression and tried to provide a solution for the real world problem. In our previous work we have described an image compression technique based on Fuzzy transform. In this paper we have done the comparative analysis of that technique, with respect to some other techniques based on the different transforms. In these techniques the most commonly used JPEG and image compression technique based on move-to-front transform, given by R. Benzid, are included. The comparison is done on the basis of PSNR (Peak Signal to Noise Ratio), MSE (Mean Square Error) and execution time.

Keywords

Fuzzy Transform, PSNR (Peak Signal to Noise Ratio), MSE (Mean Square Error), Execution Time

INTRODUCTION

With the growth of technology and entrance into the Digital Age, the world has found itself amid a vast amount of information. Dealing with such enormous information can often present difficulties. Image compression is minimizing the size in bytes of a graphics file without degrading the quality of the image to an unacceptable level. The reduction in file size allows more images to be stored in a given amount of disk or memory space. It also reduces the time required for images to be sent over the Internet or downloaded from Web pages [1-2].

With the increasing use of multimedia technologies, image compression requires higher performance as well as new features. There are many methods exists for the image compression, JPEG is one most common technique among them. The approach recommended by JPEG is a transform coding approach using the DCT [1-2]. But the JPEG is not hold completely good for the real time application as its processing time is sufficiently high. Also in the applications where high compression is required with the lossless compression of image, the JPEG can’t be applicable at all.

As a solution of first problem the image compression technique based on the fuzzy transform is proposed by us in [12]. This works sufficiently fast a compare to the JPEG. For the solution of the second problem a method is proposed in the [13]. The method is based on the move-to-front transform and two-role encoder. The lossless compression requires only for the rear applications, in the normal scenario the quality of image can be compromise up-to some extent.

IMAGE COMPRESSION USING FUZZY TRANSFORM

A transformation method on fuzzy domain called fuzzy transform (or, shortly, F-transform) that encompasses both classical transforms as well as approximation methods [3-5]. The F-transform establishes a correspondence between a set of continuous functions on an interval of real numbers and the set of n-dimensional (real) vectors [6-9]. The Approach for Image Compression, based on Fuzzy Transform, is attempted by normalizing the values of its pixels. Any image can be considered as a fuzzy matrix (relation). Image is sub divided into small blocks and compress - decompress by the use of Fuzzy transformation and inverse transformation.

The method is based on the Fuzzy transform. In this method, the image is partitioned in to sub-images of square size (16x16, 8x8, 4x4) called blocks, then any compressed sub-image is obtained using fuzzy transform and uniform quantization according to the standard deviation of sub-image. These sub-images are decompressed with the related inverse fuzzy transform and recomposed for the reconstruction of the image [12]. This method allows the user to select regions of interest and to compress each one with different quality factor [3-11].

The methodology of the method is simple enough to understand, which can be explained in the following steps:

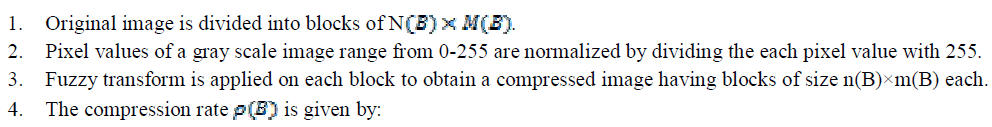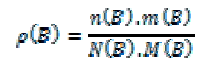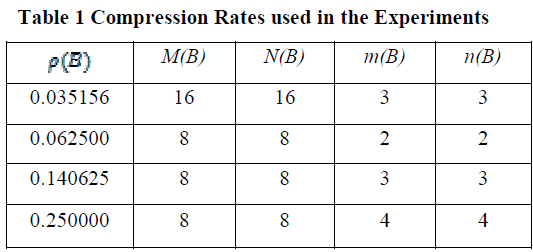5. Equation (2) is used to obtain a decompressed image of size N (B)M(B).

6. Each block is then de-normalized to get reconstructed image.

PARAMETERS

1) MSE and PSNR: Techniques that commonly employed for image compression result in some degradation of the reconstructed image. A widely used measure of reconstructed image fidelity for an N x M size image is the mean square error (MSE) and is given by:-

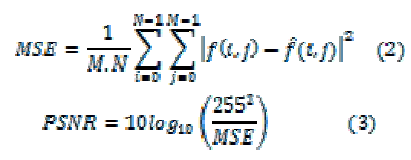2) EXECUTION TIME: The different algorithm of image compression follows the different methodology. Due to which a measurable difference is obtained in there execution time. For a method to be suitable for the run time processing, its execution time should be small. The execution time is measured in seconds.

3) COMPRESSION RATIO: For the proposed method the Compression Ratio is the inverse of the Compression Rate. For the Other methods the compression ratio can be described by the ratio of bits in the original image to the compressed image.

RESULT AND DISCUSSION

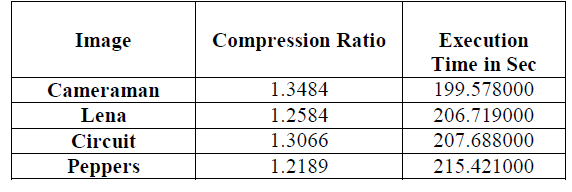
Table 2 Compression Ratio and Execution Time in sec. for different image compressed using move to front transform and two-role encoder

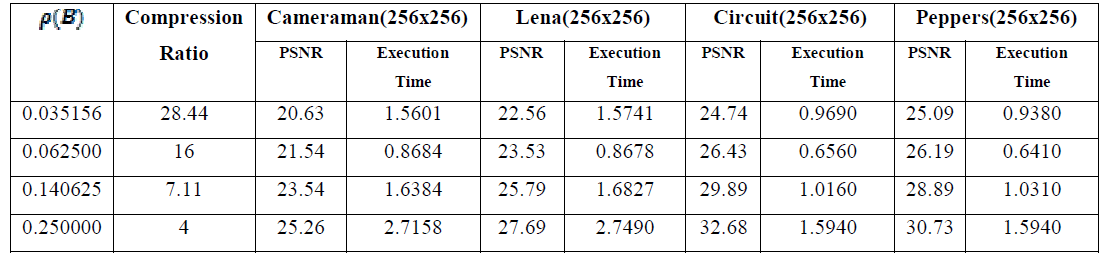
Table 3 Compression Ratio, PSNR and Execution Time in sec. for different image compressed using Fuzzy Transform.

From the obtained results, we have found that for the move to front transform based method the PSNR is infinite, but the compression ratio is very low and the execution time is sufficiently high.

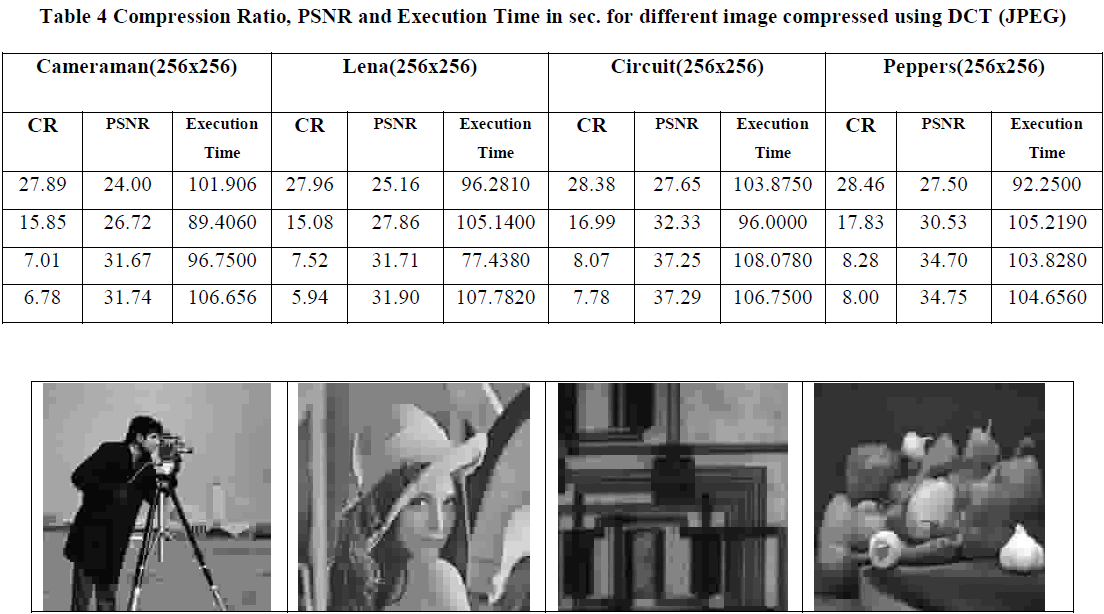
Further we have seen from the results given in table 3, that with the increment in the value of compression rate the PSNR is increasing and MSE is decreasing. The time of compression is inversely proportional to M (B).N (B) i.e. block size before compression and directly proportional to the m (b).n (b) i.e. corresponding block size after compression. From the result of image compression using DCT i.e. JPEG given in table 4, we found that the PSNR value is little bit better for the given compression ratio, But the execution time significantly high, as compare to the image compression using fuzzy transform.

CONCLUSSION

In this paper, we have discussed the requirements of the modern world and the significance of the image compression. We have seen that for any compression scheme the quality of the image after reconstruction and the time of compression and reconstruction i.e. the execution time are the two important issues.

In the move to front transform based method [13] the PSNR is infinite, means the image reconstruct exactly as original, but the compression ratio is very less and the execution time is very high i.e. in 200 seconds. So this method of compression is useful when any degradation in the quality cannot be compromised.

In the JPEG the Quality of compression is not degrade too much and it’s in except able range, but its execution time is also sufficiently high i.e. in the 100 seconds, whereas for the Fuzzy transform based technique[12] it’s near about 1second only. In this method the compression ratio is also sufficiently high with the except able PSNR value. Thus we can say that the proposed method is an ideal method for the real time image compression i.e. image uploading and downloading, high speed recording cameras etc.

For the purpose of the data compression, Fuzzy transform is a good and useful transform. In the future many other uses of fuzzy transform could be found. The image compression using the Fuzzy transform is found a novel idea. In the nearest future, further more researches can be done for the improvement in the PSNR and Compression ratio with the high speed performance in some compression method might be based on some new transform.

References

Wallace.G, "The JPEG still picture compression standard", vol.34, pp. 30-44, 1991.
G. K. Wallace, “The JPEG Still Picture Compression Standard”, IEEE Trans. On Consumer Electronics, vol.38, No.1, Feb 1992.
I. Perfilieva, “Fuzzy transforms: Theory and applications”, Fuzzy Sets and Systems, 2006, pp. 993 – 1023.
B. De Baets, R. Mesiar, T-partitions, Fuzzy Sets Systems, 1998, 211–223.
D. Dubois, H. Prade, Rough fuzzy sets and fuzzy rough sets, Internat. J. Gen. Systems, vol. 17, 1990, pp.191–209.
P. Hajek, Metamathematics of Fuzzy Logic, Kluwer Academic Publishers, Dordrecht, 1998.
Perfilieva, Fuzzy transforms and their applications to data compression, in: Proc. Int. Conf. on FUZZ-IEEE 2005, Reno, Nevada, USA, May 22–25, 2005, pp. 294–299.
I. Perfilieva, E. Chaldeeva, Fuzzy transformation, in: Proc. of IFSA’2001 World Congress, Vancouver, Canada, 2001.
K. Hirota, W. Pedrycz, Data compression with fuzzy relational equations, Fuzzy Sets and Systems, 2002, pp.325–335.
V. Loia, W. Pedrycz, S. Sessa, Fuzzy relation calculus in the compression and decompression of fuzzy relations, International Journal of Image and Graphics, vol 2, 2002, pp.1–15.
H. Nobuhara, W. Pedrycz, K. Hirota, Fast solving method of fuzzy relational equation and its application to lossy image compression, IEEE Transactions on Fuzzy Systems, vol.8, no.3, 2000, pp. 325–334.
N. Gupta, M.P. Parsai, “An image compression technique based on Fuzzy transform”, IJETT, vol. no. 2014.
R.Benzid, “Lossless compression of binary image using move-to-front transform and two-role encoder”, Electron. Letters, vol. 47, no. 2, pp. 104–105, 2011.