ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Chethan B1, Ravisimha B N2, Dr. M Z Kurian3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Digital Communication technologies provide the best communication speed and larger data capacity. Though the Digital communication is the best one, but it is also affected by noise & non-linearities. These noises cause disturbances in the channel making the data corrupt or lost. Among these disturbances Inter Symbol Interference (ISI) is the most prominent and disastrous phenomenon that cause huge data loss. This paper provides the information on how the ISI is caused and how it causes the data loss.
Keywords |
| Noise and Non-linearity, Inter Symbol Interference (ISI), FIR filter, Pulse Shaping Filter. |
INTRODUCTION |
| The digital communication systems are fast advancing techniques that are providing the mankind with the faster access to information and exchange of data in a larger scale. The channel that is used to communicate between the transmitter and the receiver is generally through open air medium. This channel is comprised of many natural phenomenon and other naturally existing signals. When the message signals are passed over such channels the data is likely to be distorted and lost during the communication process. One such disturbance is the Inter symbol Interference (ISI). |
| In order to reduce this error in communication the pulse shaping filters are designed. Among different pulse shaping filters the FIR Raised Cosine Filter is widely used in digital communication to reduce ISI. |
| In this paper, the causes for ISI, effect of ISI and the different types of pulse shaping filters that are used to reduce the ISI are discussed. |
II. INTER SYMBOL INTERFERENNCE |
| Among the different types of distortions in communication Inter Symbol Interference is a phenomenon that causes the heavy data loss in the communication. Usually the digital information that is transmitted will be in the form of square waveform representing the 1’s and 0’s. When this square waveform mixes with the noises and non linearities in the channel, the square waveform starts to spread and merge with the adjacent symbol sequence, making the data there to be unreadable. At the receiver end this data is wrongly decoded as the receiver cannot predict the correct level of the square waveform leading to the loss of information. ISI is usually caused due to multipath propagation of the signal in band limited channel and the non-linear frequency response of the channel. The Fig 1 represents the graphical representation of ISI. [11] The presence of ISI in the system introduces errors in the decision device at the receiver output. Therefore, in the design of the transmitting and receiving filters, the objective is to minimize the effects of ISI, and thereby deliver the digital data to its destination with the smallest error rate possible[1] [2] [3]. |
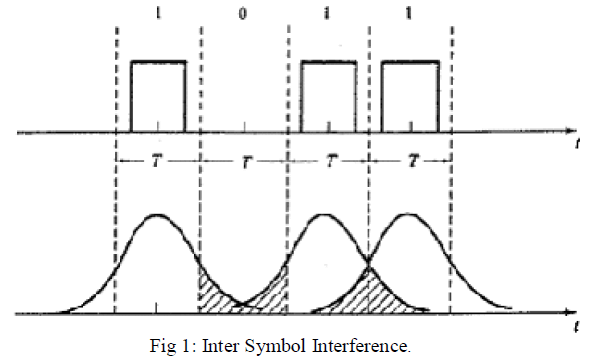 |
III. CAUSES OF INTER SYMBOL INTERFERENCE |
A. Multipath propagation |
| One of the causes of Inter Symbol Interference is multipath propagation in which a wireless signal from a transmitter reaches the receiver via many different paths. The causes of this include reflection refraction (such as through the foliage of a tree) and atmospheric effects such as atmospheric ducting and ionospheric reflection. Since all of these paths are different lengths - plus some of these effects will also slow the signal down - this results in the different versions of the signal arriving at different times. This delay means that part or all of a given symbol will be spread into the subsequent symbols, thereby interfering with the correct detection of those symbols. [11] Additionally, the various paths often distort the amplitude and/or phase of the signal thereby causing further interference with the received signal. [1] [2] [3] |
B. Band-limited channels |
| Another cause of Inter Symbol Interference is the transmission of a signal through a band-limited channel, i.e., one where the frequency response is zero above the cutoff frequency. Passing a signal through such a channel results in the removal of frequency components above this cutoff frequency; in addition, the amplitude of the frequency components below the cutoff frequency may also be attenuated by the channel [1] [2] [3]. |
C. Noises and Fading Channels |
| Noise may be defined as any unwanted signal that interferes with the communication, measurement or processing of an information-bearing signal. Noise is present in various degrees in almost all environments. For example, in a digital cellular mobile telephone system, there may be several variety of noise that could degrade the quality of communication, such as acoustic background noise, thermal noise, electromagnetic radio-frequency noise, co-channel interference, radio channel distortion, echo and processing noise. Noise can cause transmission errors and may even disrupt a communication process [7]. |
| A Communication Channel is known as fading channel if in which it has to face different fading phenomenon, during signal transmission. In real world environment, the radio propagation effects combine together and multipath is generated by these fading channels. Due to multiple signal propagation paths, multiple signals will be received by receiver and the actual received signal level is the vector sum of the all signals [5]. |
| Among the noises, the following three are the noises that widely affect the digital communication. They are Additive White Gaussian Noise (AWGN), Rayleigh Fading, and Rician Fading. These noises and fading cause huge loss of data in digital communication. And fading causes a major error called Inter Symbol Interference (ISI). |
I) Additive White Gaussian Noise Channel |
| The simplest type of channel is the Gaussian channel. It is often referred to the additive white Gaussian noise (AWGN) channel. Basically, it is the noise generated in the receiver side if we assume that the transmitter is ideal and noiseless. |
| This type of noise is assumed to have a constant power spectral density over the whole channel bandwidth and its amplitude Probability Density Function (PDF) obeys the statistics of a Gaussian distribution. [6]. Gaussian noise is very important in the analysis of communication system performance. The classical AWGN channel is always considered as the starting point to develop basic systems performance |
II) Rayleigh Fading Phenomenon. |
| In a mobile communication system, one of the most devastating phenomena is fading. Fading is the direct result of multi-path propagation where signals propagate along different paths before arriving at the receiver antenna. Rayleigh fading occurs when no Line-of-Sight (LOS) path exists in between transmitter and receiver, but only have indirect path, then the resultant signal received at the receiver will be the sum of all the reflected and scattered waves [4]. These radio signals may arrive at receiver after different delays, with different amplitudes, and with different phases. Because there are so many different received signal components, constructive and destructive interference results in fading. |
| Thus, in a multi-path fading channel, when a signal pulse is transmitted, the receiver receives the superposition of many pulses. These multi-paths cause a wide fluctuation in the received signal magnitude, which makes reliable transmission of information a challenge [6]. |
III) Rician Fading Phenomenon |
| The Rician fading phenomenon is very much similar to the Rayleigh fading phenomenon. The difference is that it occurs when there is a LOS as well as the non-LOS path in between the transmitter and receiver, i.e. the received signal comprises on both the direct and scattered multipath waves. This phenomenon also causes huge losses due to signal collision and interference making communication degraded [4]. |
IV. FINITE IMPULSE RESPONSE PULSE SHAPING FILTERS |
| Pulses are sent by the transmitter and ultimately detected by the receiver in any data transmission system. At the receiver, the goal is to sample the received signal at an optimal point in the pulse interval to maximize the probability of an accurate binary decision. This implies that the fundamental shapes of the pulses be such that they do not interfere with one another at the optimal sampling point. There are two criteria that ensure non-interference. Criterion one is that the pulse shape exhibits a zero crossing at the sampling point of all pulse intervals except its own. Otherwise, the residual effect of other pulses will introduce errors into the decision making process. Criterion two is that the shape of the pulses be such that the amplitude decays rapidly outside of the pulse interval. This is important because any real system will contain timing jitter, which means that the actual sampling point of the receiver will not always be optimal for each and every pulse. So, even if the pulse shape provides a zero crossing at the optimal sampling point of other pulse intervals, timing jitter in the receiver could cause the sampling instant to move, thereby missing the zero crossing point. This, too, introduces error into the decision making process. Thus, the quicker a pulse decays outside of its pulse interval, the less likely it is to allow timing jitter to introduce errors when sampling adjacent pulses. Oversampling can reduce the noise caused by timing jitter [8]. |
| In addition to the non-interference criteria, there is the ever present need to limit the pulse bandwidth. The rectangular pulse, by definition, meets criterion number one because it is zero at all points outside of the present pulse interval. In modern data transmission systems, bits or groups of bits (symbols) are typically transmitted in the form of individual pulses of energy. A rectangular pulse is probably the most fundamental. It is easy to implement in a real-world system because it can be directly compared to opening and closing a switch, which is synonymous with the concept of binary information [8]. |
| The next task is to decide which basic category of digital filter to use: finite impulse response (FIR) or infinite impulse response (IIR). The fundamental difference between them is the fact that the IIR contains feedback. The implication is that the response of an IIR filter to an impulse (a single nonzero sample followed by zero samples) is infinite. That is, the IIR will continue to produce non-zero output samples long after the application of an impulse. This is an undesirable consequence for data pulse transmission [9]. |
| The FIR does not suffer from this problem because its architecture does not contain any feedback elements. A single, non-zero impulse at the input will only yield output samples while the impulse propagates down the delay stages. Generally, pulse shaping filters employ FIR designs [9]. |
| There are mainly four types of filters that are commonly used in communication systems. |
a) Boxcar filters |
| A filter is said to be a boxcar filter if it employs boxcar function which is zero over the entire real line except for a single interval where it is equal to a constant, A; it is a simple step function The boxcar function can be expressed in terms of the uniform distribution as |
| Boxcar(x) = (b-a) A f (a, b; x) = H(x-a) – H (x-b), |
| where f (a, b; x) is the uniform distribution of x for the interval [a, b] and H(x) is the Heaviside step function. In Fig 2 the boxcar function is represented. |
| As with most such discontinuous functions, there is a question of the value at the transition points. These values are probably best chosen for each individual application. When a boxcar function is selected as the impulse response of a filter, the result is a moving average filter. The function is named after its resemblance to a boxcar, a type of railroad car. |
| The boxcar filter results in infinitely wide bandwidth for the signal. Thus its usefulness is limited, but it is used widely in wired baseband communications, where the channel has some extra bandwidth and the distortion created by the channel can be tolerated [11]. |
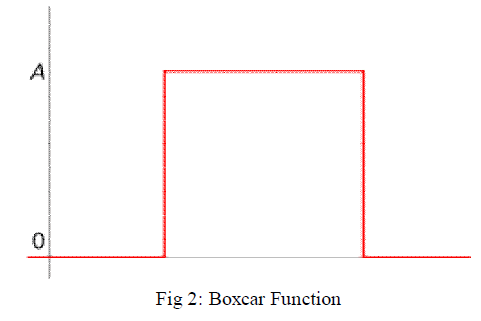 |
b) Sinc Filters |
| In signal processing, a sinc filter is an idealized filter that removes all frequency components above a given cutoff frequency, without affecting lower frequencies, and has linear phase response. The filter's impulse response is a sinc function in the time domain, and its frequency response is a rectangular function. It is an ideal low-pass filter in the frequency sense, perfectly passing low frequencies, perfectly cutting high frequencies; and thus may it be regarded to be a brick-wall filter [11]. |
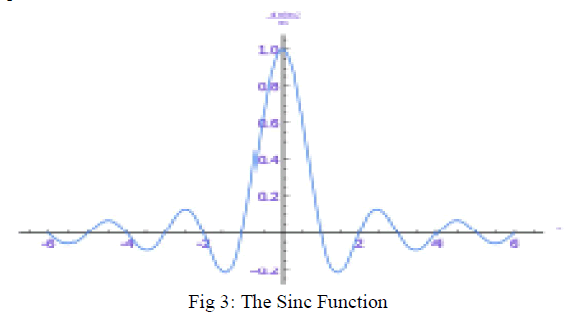 |
| Theoretically the best pulse shaping filter would be the sinc filter, but it cannot be implemented precisely. In Fig 3, The Sinc function is represented. It is a non-causal filter with relatively slowly decaying tails. It is also problematic from a synchronization point of view as any phase error results in steeply increasing Inter Symbol Interference. [11] |
c) Gaussian Filter |
| Gaussian filters are significantly better than RRC filters. Gaussian waveform, which is optimum in terms of energy concentrations in time and frequency domains, has a large ISI. Pulse shaping filters are normally implemented as oversampled finite impulse response (FIR) digital filters. In signal processing, oversampling is the process of sampling a signal with a sampling frequency significantly higher than twice the bandwidth or highest frequency of the signal being sampled. Oversampling helps avoid aliasing, improves resolution and reduces noise. The FIR Gaussian pulseshaping filter design is done by truncating a sampled version of the continuous-time impulse response of the Gaussian filter [8]. |
d) Raised Cosine Filter |
| Raised-cosine filters are practical to implement and they are in wide use. They have a configurable excess bandwidth, so communication systems can choose a tradeoff between a simpler filter and spectral efficiency [10] [11]. |
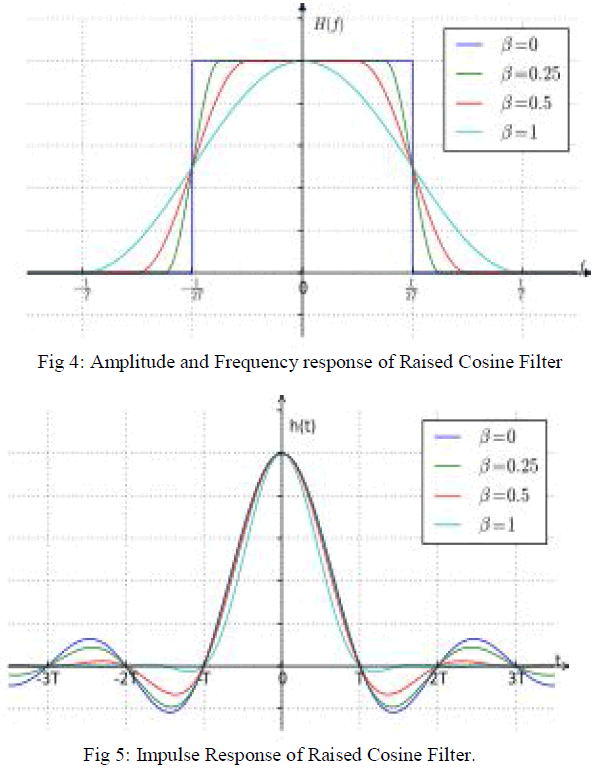 |
| The raised-cosine filter is a filter frequently used for pulse-shaping in digital modulation due to its ability to minimize Inter Symbol Interference (ISI). Its name is derived from the fact that the non-zero portion of the frequency spectrum of its simplest form (β=1) is a cosine function, 'raised' up to sit above the f (horizontal) axis. The efficiency of the filter varies with the value of Roll-off factor (β) which varies from ‘0’ to ‘1’. In Fig 5, impulse response representation of the filter for different values of β is shown [10] [11]. |
Roll off factor |
| The roll-off factor, β, is a measure of the ‘excess bandwidth’ of the filter, i.e. the bandwidth occupied beyond the Nyquist bandwidth of 1/2T. If we denote the excess bandwidth as ‘Δf’, then: |
 |
CONCLUSION |
| Inter Symbol Interference (ISI) is an inevitable consequence that cannot be totally avoided. in this paper, the topics of how ISI is generated in channel, causes and reasons for ISI and the remedy to avoid and reduce this ISI are discussed. Also this paper provides the discussions of different type of FIR Pulse Shaping filters are presented among which the Raised Cosine Filter is the most advantageous due to the fact that it is easy for practical implementation. |
References |
|