ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Mohammad Shahnawaz Nasir1, Dr. R B S Yadav2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
The effectiveness of mining association rules is a significant field of Knowledge Discovery in Databases (KDD). The Apriori algorithm is a classical algorithm in mining association rules. This paper presents an improved method for Apriori and Frequent Pattern algorithms to increase the efficiency of generating association rules. This algorithm adopts a new method to decrease the redundant generation of sub-itemsets during pruning the candidate itemsets, which can form directly the set of frequent itemset and remove candidates having a subset that is not frequent in the meantime. This algorithm can raise the probability of obtaining information in scanning database and reduce the potential scale of itemsets
KEYWORDS |
| Association rule, Apriori algorithm, Frequent Pattern algorithm, Frequent itemset |
I. INTRODUCTION |
| Recent advancements in technology provide an opportunity to construct and store the huge amount of data together from many fields such as business, administration, and banking, the delivery of social and health services, environmental safety, security and in politics. Typically, these data sets are very huge and regularly growing and contain a huge number of compound features which are hard to manage. Therefore, mining or extracting association rules from large amount of data in the database is interested for many industries which can help in many business decision making processes, such as cross-marketing, basket data study, and promotion assortment. Frequent Itemset Mining (FIM) is one of the most well known techniques which is concerned with extracting the information from databases based on regularly occurring events, i.e., an event, or a set of events, is interesting if it occurs frequently in the data, according to a user given minimum frequency threshold or in other terms it is a non-supervised process which concerns in finding frequent patterns (or itemsets) hidden in large volumes of data in order to produce compressed summaries or models of the database. It is the fundamental operation behind several common data-mining tasks including association rule [1] and sequential pattern mining [2]. |
| Mining association rule is one of main contents of data mining research at present, and stress particularly finding the relation of different items in the database. It is an important aspect in improving mining algorithm that how to decrease itemsets candidate in order to generate frequent itemsets efficiently. In classical Apriori algorithm, when candidate generations are generated, the algorithm needs to test their occurrence frequencies. The manipulation with redundancy result in high frequency in querying, so tremendous amounts of resources will be expended whether in time or in space. |
| In this paper, an improved algorithm for extracting association rules that considers the time, number of database scans, memory utilization and the interestingness of the rules. The proposed scheme which is combination of present maximal Apriori (improved Apriori) and Frequent Pattern-tree techniques (FP tree) that guarantees the better performance than classical Apriori algorithm. The aim of the proposed techniques are, analyze the mining frequent itemsets and evaluate the performance of new techniques and compare with the existing classical Apriori and Frequent Pattern-tree algorithm with support count. |
II. RELATED WORK |
| Frequent pattern mining is the classification of frequent itemsets from huge database. The major goal of frequent itemset mining is to recognize all frequent itemsets, that is, itemsets that have at least a particular minimum support; the percentage of transactions containing the itemset [3]. The rationale behind using support is that only itemsets with high frequency are of interest to users, “the practical usefulness of the frequent itemset mining is restricted by the significance of the discovered itemsets”. The AIS algorithm put forth by Agrawal et al. [1] in which only one item consequent association rules are generated, which means that the consequent of those rules only contain one item. To make this algorithm more effective, an estimation method was introduced with an intention to diminish those itemsets candidates that have no hope to be large, as a result unnecessary effort of counting those itemsets can be avoided. Since all the candidate itemsets and frequent itemsets are assumed to be stored in the main memory, memory management is also proposed for AIS when memory is not sufficient. SETM algorithm created by Houtsma and Swami et al. [4] motivated by the wish to use SQL to compute large itemsets. Like AIS, SETM algorithm candidate itemsets are generated on the fly as the database is scanned but counted at the end of the pass. It thus generates and counts every candidate itemset that the AIS algorithm generates. J. S. Park, M. Chen, P.S. Yu.et al. [5] described DHP algorithm in which author utilizes the extra data structure i.e., Hash Bucket for candidate itemset generation. The algorithm is an effective hash-based algorithm for the candidate set generation. Han et al. [6] devised an FP-growth method that mines the complete set of frequent itemsets without candidate generation. The algorithm does not subscribe to the generate-and-test paradigms of Aprori. Instead, it encodes the data set using a compact data structure called FP-tree and extracts frequent itemsets directly from this structure. The algorithm adopts divide and conquer strategy. A memory-based, efficient patterngrowth algorithm, H-mine (Mem), is for mining frequent patterns for the datasets that can fit in (main) memory. H-mine [7] algorithm is the enhancement over FP-tree algorithm as in H-mine projected database is shaped using in-memory pointers. H-mine uses an H-struct new data structure for mining purpose known as hyperlinked structure. It has polynomial space complexity therefore more space efficient then FP-growth and also designed for fast mining purpose. Mining quantitative association rules based on a statistical theory to present only those that deviate substantially from normal data was studied by Aumann and Lindell et al. [8]. Zhang et al. [9] considered mining statistical quantitative rules. Statistical quantitative rules are quantitative rules in which the right hand side of a rule can be any statistic that is computed for the segment satisfying the left hand side of the rule. |
III. ASSOCIATION RULES DESCRIPTION |
| The association rule mining was first proposed by Agrawal and et al[10]. It can be formally defined as follow: Given a transaction database DB, I={il, i2, i3, … , in} is a set of items with n different itemsets in DB, each transaction T in DB is a set of item (i.e. itemsets). |
| Definition 1: Let I={il, i2, i3, … , in} be a set of items, then D={<Tid, T>|T⊆I} is a transaction database, where Tid is an identifier which be associated with each transaction. T⊆I. |
 |
| Classical Apriori algorithm: |
| (1) Cl = {candidate I-itemsets}; |
| (2) L1 = {c∈ C1|c.countKminsup}; |
| (3) FOR (k=2;Lk-1LM;k++) DO BEGIN |
| (4) Ck=apriori-gen(L k-1); |
| (5) FOR all transactions t∈ D DO BEGIN |
| (6) Ct=subset (Ck,t); |
| (7) FOR all candidates c∈Ct DO |
| (8) c.count++; |
| (9) END |
| (10) Lk={c∈Ck |c.countKminsup} |
| (11) END |
| (12) Answer=∪Lk; |
| The association rule mining is a two-step process: |
| 1. Find all the frequent itemsets in the transaction database. If support of itemset X, support(X) Kminsup, then X is a frequent itemset. Otherwise, X is not a frequent itemset. |
| 2. Generate strong association rules from frequent itemsets. For every frequent itemset A, if B⊂A, BLM, and support (A) / support(B) Kminconf, then we have association rule B⇒ (A-B). The second step is relatively easy, and its algorithm generation can be found in the reference. The present focuses in research are to find highly efficient algorithms in the first step. |
IV. PROBLEM DESCRIPTION |
| In Apriori algorithm, from Ck to Lk have two steps: (1) Pruning itemsets according to Lk-1. (2) Pruning itemsets according to minsupport. |
| First, the set of frequent 1-itemsets is found. This set is denoted L1. L1 is used to find L2, the set of frequent 2- itemsets, which is used to find L3, and so on, until no more frequent k-itemsets can be found, and then algorithm ceases. In the cycle k, a set of candidate k-itemsets is generated at first. This set of candidates is denoted Ck. Each itemset in Ck is generated by joining two frequent itemsets that belong to Lk-1 and have only one different item. The itemsets in Ck are candidates for generating frequent sets, and the ultimate frequent itemsets Lk must be a subset of Ck. Every elements in Ck should be identified in business database to decide wither to join Lk. |
| The question of Apriori algorithm is that the set of candidate itemsets Ck is generated from Lk-1. Every itemset in Ck is tested whether its all k-l subsets constitute a large k-1 itemset or not, if one of k-1 itemsets is not in Lk-1 itemsets, the super itemset of this k-l itemset can be deleted. That is, every time a k itemset is constituted, Apriori must scan all Lk-1 itemsets. Because of many scan large database many times in this way, the identifying processes are the bottleneck of the Apriori algorithm. |
| Apriori algorithm may need to generate a huge number of candidate generations. Each time when candidate generations are generated, the algorithm needs to judge whether these candidates are frequent item sets. The manipulation with redundancy result in high frequency in querying, so tremendous amounts of resources will be expended whether in time or in space. |
| FP-Growth Algorithm |
| FP-growth algorithm considered to be most helpful and efficient method for mining all frequent itemsets without candidate„s generation. FP-growth uses a combination of the vertical and horizontal database layout to store the database in main memory. Instead of storing the cover for every item in the database, it stores the actual transactions from the database in a tree structure and every item has a linked list going through all transactions that enclose that item. This new data structure is denoted by FP-tree [10]. Every node additionally stores a counter, which keeps track of the number of transactions that share the branch through that node. Also a link is stored, pointing to the next occurrence of the respective item in the FP-tree, such that all occurrences of an item in the FP-tree are linked together. Inspite of this, a header table is used which contains each separate item together with its support and a link to the first occurrence of the item in the FP tree. In the FP-tree, all items are set in support descending order, because in this way, it is predictable that this representation of the database is kept as small as possible since all more regularly occurring items are arranged closer to the root of the FP-tree and thus are more likely to be shared. |
| The algorithm employs divide and conquer strategy for mining the frequent itemsets which are as follows: FP-growth first compresses the database representing frequent itemset into a frequent-pattern tree, or FP-tree, which retains the itemset association information as well. The next step is to divide a compressed database into set of conditional databases (a special kind of projected database), each associated with one frequent item. Finally, mine each of such databases separately. Particularly, the construction of FP-tree and the mining of FP-tree are the main steps in FP-growth algorithm. |
| Comparative study between Apriori and FP-Growth |
| The following table shows the differences between Apriori and FP-growth. |
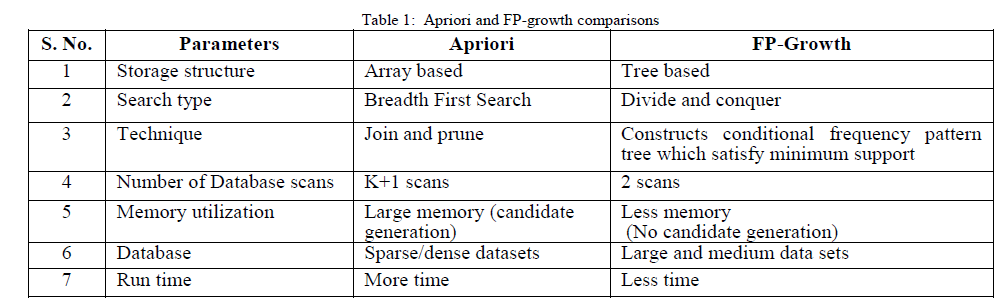 |
V. IMPROVED ALGORITHM |
| The proposed algorithm is based on improved Apriori and the Frequent Pattern-tree structure with support count is there. In a huge transactional database like retailer database it is quite common that several items has been sale or purchase at the same time therefore the database must contains various transactions which include same set of items. Thus by taking benefits of such type of transactions, it has to be discover out, the frequent itemsets and prune the database at the initial without generating the candidate itemset and numerous database scan, which results in efficiently utilization of memory and also enhanced computation. |
| The proposed algorithm is based on the Apriori property i.e., all non empty subsets of the frequent itemsets are frequent. It has two procedures. In first procedure, locate those transactions which are frequently appearing in the database equal to or greater than min user defined support which is known as maximal frequent itemset. Then get all nonempty subsets of those maximal frequent itemset as frequent according to Apriori property. Examine the database to find 1-itemset frequent elements. Then it has to be found out as a lot of items which are 1-itemset frequent but not contain in maximal frequent transactions. Therefore trim the database by considering only those transactions which contain 1-itemset frequent elements from the database, but not include in the maximal frequent itemsets. Obviously the size of the trimmed or pruned database is smaller as compared to actual database in the average cases and no item left in best case. |
| For the second procedure, the trimmed database is taken as input and then again examines the trimmed database once in order to find 1-itemset frequent and eliminate those items from transaction which are not 1-itemset frequent. Then create the Frequent Pattern tree only for trimmed transactions. In this manner it reduces the memory problem for Frequent Pattern-tree because the size of the database is compact in most of cases. In best case it does not require to construct the Frequent Pattern-tree because all elements are searched in first procedure. In the worst case if there is no maximal frequent transaction exist, then only second procedure run and also computational performance is same as Frequent Pattern-tree[11]. The basic objective behind this concept is to trim the database after searching or finding the maximal frequent itemsets and construct the Frequent Pattern-tree for a pruned database thus reduce memory problem in FP-tree and make the mining process fast. The steps in more detail are as follows: |
| Algorithm in Detail |
| Procedure 1: |
| Input: Database D, minimum support |
| Step 1: Take a 2- dimensional array; Place the transaction into 2-dimmension array with their count of repetition. |
| Step 2: Position them in increasing order on the basis of the pattern length of each transaction. |
| Step 3: Search the maximal transactions (k-itemset) from the array whose count is greater than or equal to the minimum support known as maximal frequent itemsets or transactions. If k-itemsets count is less than minimum support then look for k-itemsets and (k-1)-itemsets jointly for next (k-1) maximal itemsets and so on until no itemsets count found greater than minimum support. If no such transaction found then go to Procedure 2. |
| Step 4: Once the maximal frequent transactions found, than according to Apriori property consider all its non empty subsets are frequent. |
| Step 5: There are itemsets remaining which are not included in maximal frequent itemset but they are frequent. Therefore discover all frequent 1-itemset and prune the database just considering only those transactions which contain frequent 1-itemset element but not include in maximal frequent transaction. |
| Output: some or all frequent itemsets, Pruned database D1. |
| Procedure2: |
| Input: Pruned database D1, minimum support |
| Step 1: Search the frequent 1-itemset from pruned database; remove all those items which are not 1-itemset frequent. |
| Step 2: Build FP-tree for mine remaining frequent itemset by following the procedure of FP-tree algorithm. |
| Output: Remaining frequent itemsets |
VI. EXPERIMENT RESULTS |
| This is an example based on the transaction database, D, of Table 2. There are ten transactions in this database, that is, |D|=10. We use the improved Apriori algorithm for finding frequent itemsets in D. Suppose the minimum support is 2. |
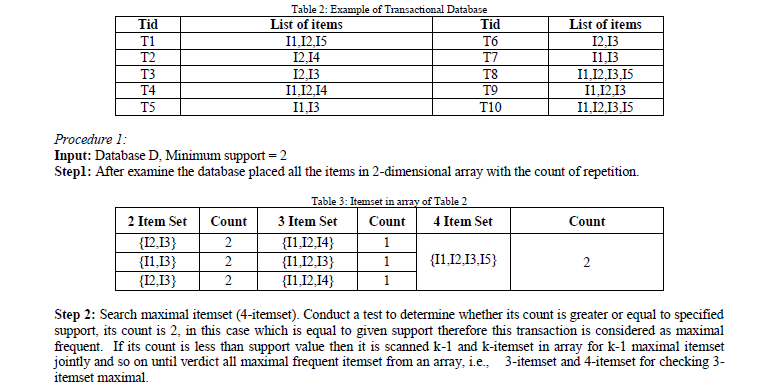 |
| Step 3: According to Apriori property subset of maximal frequent itemset is also considered as frequent, i.e., Maximal frequent itemset: {I1, I2, I3, I5}. All subsets are frequent (Apriori Property) i.e., {I1, I2, and I3}, {I1, I2, I5}, {I2, I3, I5}, {I2, I3}, {I2, I5}, {I1, I2}, {I1, I3}, {I1, I5}, {I3, I5}, {I1}, {I2}, {I3}. |
| Step 4: Examine the database for searching the above mined support. |
| Step 5: Find 1-itemset frequent from database, it is found that I4 which is frequent but not include in maximal frequent itemset. (There may be many items remain which are not include in maximal frequent itemsets, in our case only 1 item is there). Trim the database by considering only transaction which contains I4 itemset. |
| Output: Some frequent itemsets ({I1, I2, I5}, {I2, I3, I5}, {I2, I3}, {I2, I5}, {I1, I2}, {I1, I3}, {I1, I5}, {I3, I5}, {I1}, {I2}, {I3}), Pruned database shown in table 13. |
 |
| Procedure2: |
| Input: Pruned database, minimum support = 2 |
| Step 1: Find the frequent 1-itemset from trimmed or pruned database with support = 2, It is found I1 is not frequent therefore remove it. |
 |
| Transactions become: T2: I2, I4 and T4: I2, I4. |
| Step 2: Build FP-tree for remaining transaction in pruned database. |
| 1. In this case I2 and I4 having the same frequency, therefore it is no need to put in L order (descending order of their frequencies). |
| 2. A new branch is constructed for each transaction. In this case single branch is created because of same set of transactions. |
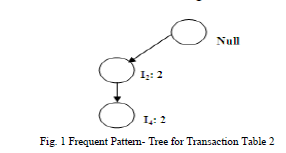 |
| 3. Construct conditional pattern base and FP – tree only for item I4. |
| Item -> I4; Pattern base ->I2: 2; Frequent Pattern tree-> I2:2, Frequent Itemset-> I4, I2 :2 |
 |
| Thus by applying above mentioned procedure it can easily found, the unmined frequent itemset i.e., {I4, I2} which some of the earlier algorithms [12] are not able to find. Now all the frequent itemset in a particular database are got. |
| Output: remaining itemsets ({I4, I2}) |
| Thus the remaining frequent itemsets which are not mined by only maximal frequent itemsets are mined by the FP growth procedure without generation of candidate itemsets and also in efficiently utilization of memory because after pruning whole database is easily fit into the memory. |
| In the next section, we demonstrate the experiments that we have performed to examine the efficiency of new procedure. For the assessment we have conducted several experiments by using the existing data set. These experiments were performed on computer with Core 2 Duo 2.00 GHZ CPU, 2.00 GB memory and hard disk 80 GB. All the algorithms were developed in C++ language and for the unit of measuring the time and the memory are second and megabyte respectively. |
| Comparison Analysis |
| Time Comparison |
| As a result of the investigational study, revealed the performance of our new technique with the Apriori and FPGrowth algorithm. The run time is the time to mine the frequent itemsets. The experimental result of time is shown in Figure 2. It reveals that the projected scheme outperforms the FP-growth and the Apriori approach. |
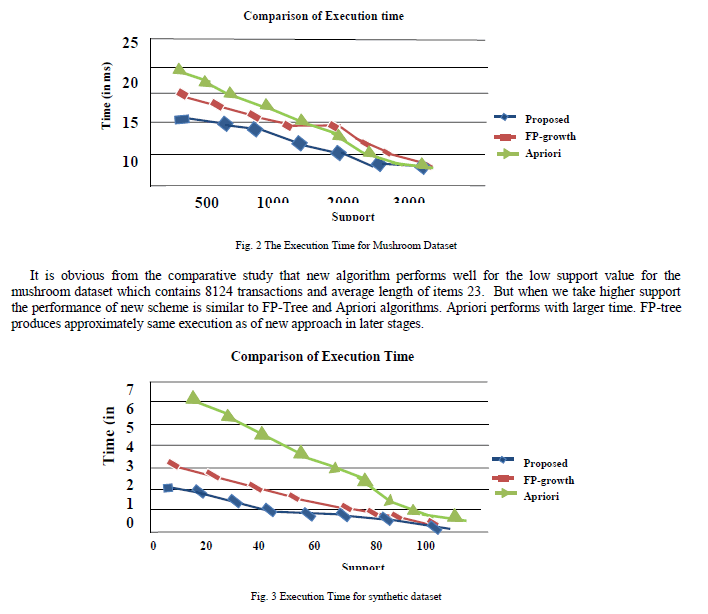 |
| For the synthetic dataset which contains the maximal frequent itemset in huge amount shows better result with new approach as shown in Figure 3 then FP-tree and Apriori algorithm. In the synthetic dataset there are different transactions consider which happen repeatedly in the database and some transactions happen greater than the minimum support. The itemset remains for mining frequent itemset are mined with the help of second procedure whose complexity equals to the FP-Growth algorithm but due to procedure 1 the overall complexity reduce and become efficient. |
| Memory Comparison |
| As it is clear from Figure 4, the memory consumption of Apriori algorithm is advanced at all level support because it produces candidate itemsets. The memory consumption for FP-tree at advanced support levels is nearby same as the new approach because as the support increase the possibility for searching the maximal itemset whose repetition is greater than the minimum support is less thus its working is approximately same as the FP-Growth algorithm. |
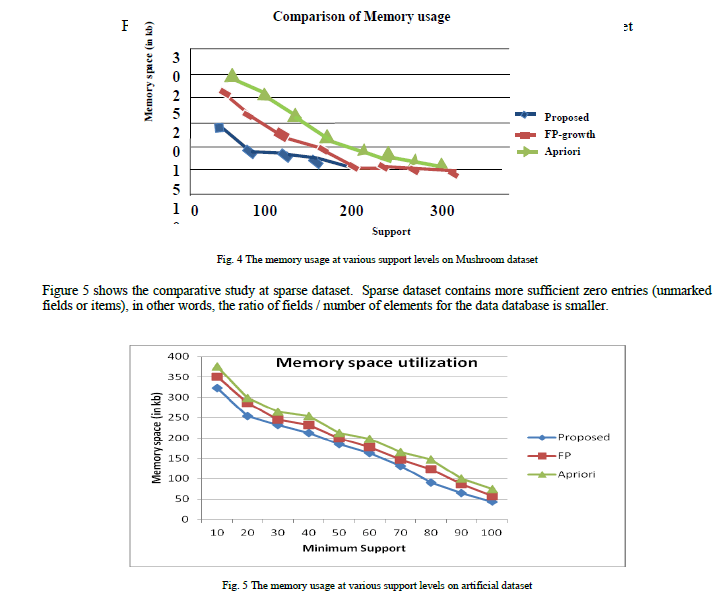 |
| Since the Apriori algorithm stores and processes only the non-zero entries, it takes the remuneration of pruning most of the uncommon items during the first few passes. Therefore at higher level support the performances of new scheme and Apriori are closer. But at lower levels it shows that new approach performs well at all support level in utilization of memory. In this case Apriori consume more memory than the FP-Tree and new approach due to its candidate generation problem. FP-tree approach performs better than the Apriori but not than the new approach. |
VII. CONCLUSION |
| In this paper, we considered time and memory utilization as factors for creating our proposed algorithm. Several experiments have been done to assess the performance of proposed scheme against FP-growth and Apriori, for generating the association rules. According to observations, the performances of the algorithms are strongly depends on the support levels and the features of the data sets (the nature and the size of the data sets) and guaranteed the time saving and the memory in the case of sparse and dense data sets. Thus this algorithm produces frequent itemsets completely. This approach does not create candidate itemsets and building FP-tree only for pruned database that fit into main memory easily. Thus it saves much time and space and considered as an efficient algorithm. |
| For both data sets the running time and memory utilization of the proposed algorithm out performed Apriori. Whereas the running time the proposed algorithm performed well over the FP-growth on the collected data set at the lower support level where probability of verdict maximal frequent itemsets is large and at higher lever running time is approximately same as the FP-Tree. The memory utilization is also approximately same as the FP-Tree at higher support and performed well at lower support. Owing to the improved algorithm mines frequent itemsets without candidate generation, the query frequency falls to about half level comparing with Apriori algorithm. The size of database is reduced; meanwhile, the storage space and computing time are saved. |
References |
|