ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Dr. Hani M. Baniodeh1, Dr. Saad Muftah Zeid2, Dr. Abdaslam Eajal3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
The DG is a new member in distribution systems that enhances the system performance. The DG improves voltage profiles, reduces real power losses, release the system capacity, increases the system reliability, delay the infrastructure upgrading, and environmentally friendly compared to the traditional power sources. Achieving the aforementioned benefits requires\installing the DGs in the appropriate location with the appropriate size. Integrating DGs in\distribution systems is an optimization problem with constraints imposed by the system\planner. This optimization problem can solved by deterministic optimization techniques such as sequential quadratic programming (SQP) or heuristic optimization techniques such as\particle swarm optimization (PSO). The PSO is a relatively new optimization technique that\mimics the bird flocking and fish schooling. A hybrid PSO-based solution technique is developed to solve the problem at hand. The proposed technique is validated on 69-bus test\system. The results obtained clearly indicate the efficiency of the developed approach in finding the optimal location and size of DG.
Keywords |
| generation, distribution ,radial, particle, swarm optimization, heuristic. |
I- DG INTEGRATION PROBLEM |
| DG is gaining increasing popularity as a viable element of electric power systems. The presence of DG in power systems may lead to several advantages such as supplying sensitive loads in case of power outages, reducing transmission and distribution networks congestion, and improving the overall system performance by reducing power losses and enhancing voltage profiles. Recent awareness of conventional/traditional thermal power plants and harmful impacts on the environment and the urge to find more environmentally friendly substitutes for electrical power generation, rapid advances made in renewable energy technologies, and the attractive and open electric power market are a few major motives that led to the high penetration of DG in most industrial nations power grids. To achieve the most from DG installation, special attention must be made to DG placement and sizing. The problem of optimal DG placement and sizing is divided into two subproblems: Where is the optimal location for DG placement and how to select the most suitable size? Many researchers proposed different methods such as analytic procedures as well as deterministic[1-6) and heuristic[7-13] methods to solve the problem. |
| In most of the reviewed literature work on the DG deployment problem, the problems of DG optimal sizing and placement were not simultaneously addressed due to the difficult nature of the problem as it combines respectively discrete and continuous variables for potential bus locations and DG sizing in a single optimization problem. This combination creates a major difficulty to most derivative-based optimization techniques and it increases the feasible search space size considerably. In this thesis, the DG sizing subproblem is solved using an improved SQP deterministic method; while the two subproblems are addressed simultaneously via an enhanced PSO metaheuristic algorithm. |
II-INTRODUCTION |
| The PSO method is employed here to deal with DG planning in the distribution networks. When DGs are to be deployed in the grid, both the DG placement and the size of the utilized DG units are to be carefully planned for. The DG planning problem consists of two steps, finding the optimal placement bus in the DS grid as well as the optimal DG size. The DG to be installed has to minimize the DS active power losses while satisfying both equality and inequality constraints. In this chapter, the PSO metaheuristic optimization method is used to solve for the optimal placement and the DG rating simultaneously, to reveal the optimal location bus in the tested DS and optimal DG rating for that location. |
III-PROBLEM FORMULATION |
| In the PSO-based approach, the DG integration problem is formulated as a mixed integer nonlinear optimization problem subject to highly nonlinear equality and inequality constraints. The objective function to be minimized in the DG placement and sizing problem is the distribution network active power losses and formulated |
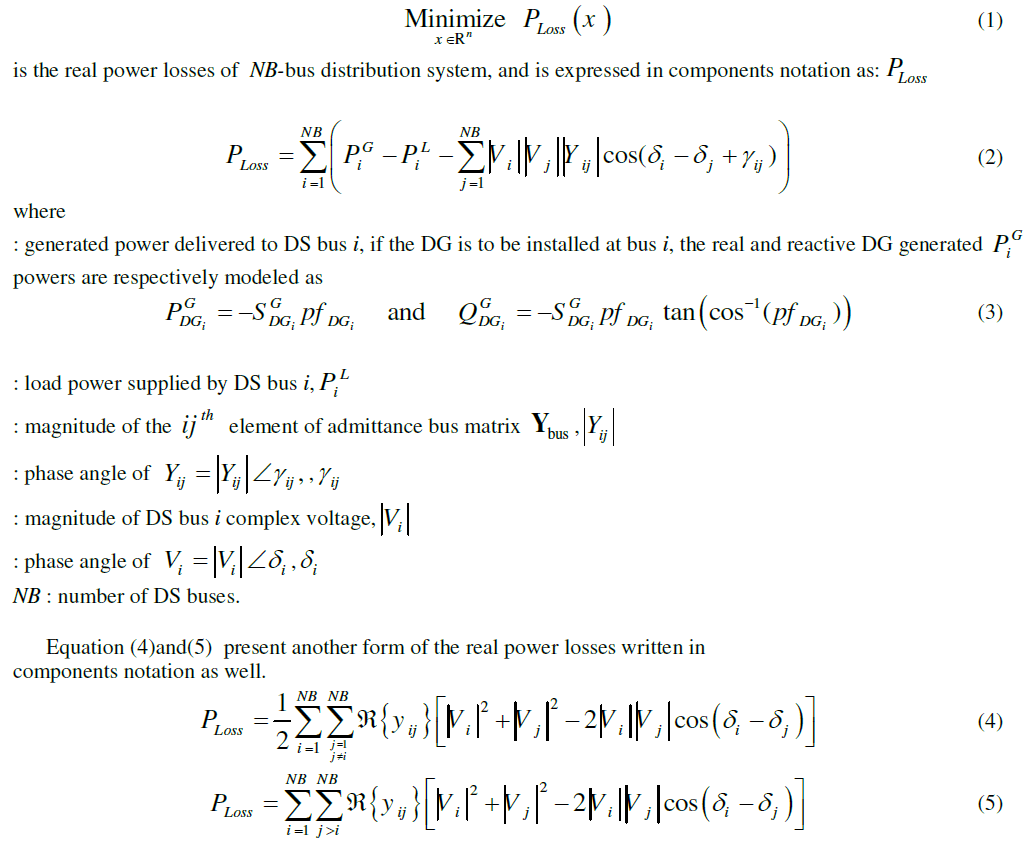 |
 |
V-INEQUALITY CONSTRAINTS |
| There are two sets of inequality constraints to be satisfied. The boundary constraints imposed on the system are the first set and they consist of the DS bus voltage magnitudes and angles, and the DG power factor. The bus voltage magnitudes and phase angles are bounded between two extreme levels imposed by physical limitations. It is customary to tolerate the variation in voltage magnitudes in the distribution level to be in the vicinity of ±10% of its nominal value [15;16]. The DG power factor is allowed for values within upper and lower limits determined by the type and nature of the DG to be installed in the distribution network. Such restrictions are expressed mathematically as shown in Eqs(12)- (14) |
 |
 |
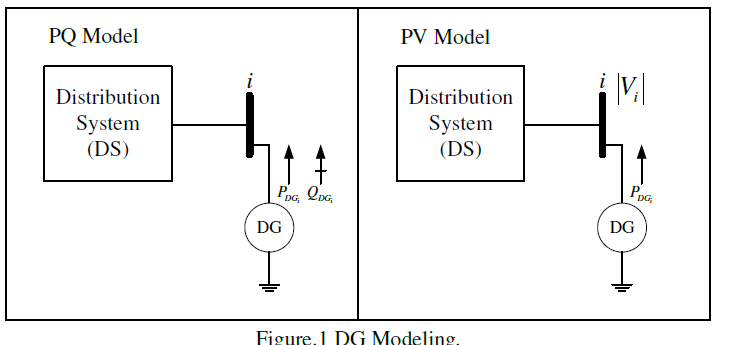
VI-DG MODELING |
| Different models were proposed in the literature to represent the DG in the distribution networks. The most common representations for conventional generating units used are the PV-controlled bus and the PQ-bus models. A DG could be modeled as a PV bus if it is capable of generating enough reactive power to sustain the specified voltage magnitude at the designated bus. The CHP type of DG has the capability of satisfying such requirement. However, it is reported that such an integration may cause a problematic voltage rise during low load intervals in the distribution system section where the DG is integrated [17]. The IEEE Std 1547-2003 stated that '' The DR shall not actively regulate the voltage at the point of common coupling (PCC) '', that is at the bus to which the DG is connected [18]. This implies that the DG model is represented by injecting a constant real and reactive power at a designated power factor into a distribution bus regardless of the system voltage [19] , i.e. as a negative load [20] . The PQ-model is widely used in representing the DG penetration into an existing distribution grid [21-23]. Most DGs customarily operate at a power factor between 0.80 lagging and unity [24;25]. |
 |
| The PSO-based approach is designed to handle single and multiple DG sitting and sizing with specified and unspecified power factors. The DG unit size variables are continuous, while the variables that represent the DG bus locations are positive integers. The DG source optimized variables are its own real power output, DG P , along with the its power factor, DG pf , and they are expressed as: |
 |
VII-PROPOSED HPSO CONSTRAINTS HANDLING MECHANISM |
| Two types of constraints in the PSO DG optimization problem are to be handled; the inequality and the equality constraints in addition to constrain the DS bus location variables to be closed and bounded positive integer set. The following subsections discuss them in turn. |
VIII-INEQUALITY CONSTRAINTS |
| The obtained optimal solution of a constrained optimization problem must be within the stated feasible region. The constraints of an optimization problem, in the context of EAs and PSO methods, are handled via methods that are based on penalty factors, rejection of infeasible solutions and preservation of feasible solutions, as well as repair algorithms [26-28]. Coath and Halgamuge [29] reported that the first two methods when utilized within PSO in solving constrained problems yield encouraging results. The penalty factor method transforms the constrained optimization problem to an unconstrained type of optimization problem. Its basic idea is to construct an auxiliary function that augments the objective function or its Lagrangian with the constraint functions through penalty factors that penalize the composite function for any constraint violation. In the context of power systems, Ma et al. [30] used this approach for tackling the environmental and economic transaction planning problem in the electricity market. He et al. [31] and Abido [32] utilized the penalty factors to solve the optimal power flow problem in electric power systems. Papla and Erlich [33] utilized the same approach to handle the unit commitment constrained optimization problem. The drawback of this method is that it adds more parameters and moreover such added parameters must be tuned and adjusted in every single iteration so as to maintain a quality PSO solution. A subroutine that assesses the auxiliary function and measures the constraint violation level, followed by evaluating the utilized penalty function, adds computational overhead to the original problem. Rejecting infeasible solutions method does not restrict the PSO solution method outcomes to be within the constrained optimization problem feasible space. However, during the PSO iterative process, the invisible solutions are immediately rejected, deleted or simply ignored and consequently new, randomly initialized position vectors from the feasible space replace the rejected ones. Though such a re-initialization process gives those particles a chance to behave better, it destroys the previous experience that each particle gained from flying in the solution hyperspace before violating the problem boundary[27]. Preserving feasible solutions method, on the other hand, necessitates that all particles should fly in the problem feasible search space before assessing the optimization problem objective function. It also asserts that those particles should remain within the feasible search space and any updates should only generate feasible solutions[27]. Such a process might lead to a narrow searching space[29] . The repair algorithm was utilized widely in EAs, especially GA, and they tend to restore feasibility to those rejected solutions, i.e. infeasible. This repair algorithm is reported to be problem dependent and the process of repairing the infeasible solutions is reported to be as difficult and complex as solving the original constrained optimization problem itself [34;35] In this project, the DG inequality constraints concerning the size, and the bus location, are to be satisfied in all the HPSO iterations. The particles that search for optimal DG locations and sizes must fly within the problem boundaries. In the case of an inequality constraint violation, i.e. the particle flew outside the search space boundaries, the current position vector is restored to its previous corresponding pbest value. By asserting that all particles are first initialized within the problem search space and by resetting the violated position vector elements to their immediate previous pbest values, the preservation of feasible solutions method is hybridized with the rejection of infeasible solutions method. That is, while preserving the feasible solutions produced by the PSO particles, the swarm particles are allowed to fly out of the search space. Nevertheless, any particle that flies outside the feasible Solution search space is not deleted or penalized by death sentence in in a way, they are kept 'energetic' and 'anxious' to continue the on-going optimal solution finding journey starting from their restored, best previously achieved feasible solution. AlHajri et al. used the hybridized handling mechanism in the PSO formulation to solve for the DG optimal location and sizing constrained minimization problem [36; 37]. |
IX-EQUALITY CONSTRAINTS |
| The power flow equations that describe the complex voltages at each bus, as well as the power flowing in each line of the distribution network, are the nonlinear equality constraints that must be satisfied during the process of solving the DG optimization problem. One of the most common ways to compute the power flow is to use the NR method. This method is quite popular due to its fast convergence characteristics. However, distribution networks tend to have a low X/R ratio and are radial in nature which poses convergence problems to the NR method. Thus, a radial power flow method, i.e. FFRPF is adopted within the proposed PSO approach to compute the distribution network power flow. A key attractive feature of this method is its simplicity and suitability for distribution networks since it mainly relies on basic circuit theorems, i.e. Kirchhoff voltage and current laws. The PSO algorithm is hybridized with the FFRPF solution method to handle the nonlinear power flow equality constraints. That is, FFRPF is used as a sub-routine within the PSO structure. By hybridizing the classic PSO with 1) the hybrid inequality constraints handling mechanism, and 2) with the FFRPF technique for handling the equality constraints, the resultant Hybrid PSO technique (HPSO) is used in tackling the DG optimal placement and sizing constrained mixed-integer nonlinear optimization problem. |
X-DG BUS LOCATION VARIABLES TREATMENT |
| The DG bus location is an integer variable previously defined in Eq.(22) to ensure that the bus, where the power to be injected, is within its imposed limits, a rounding operator is incorporated within the HPSO algorithm to round the bus value to the nearest real positive integer. That is, in each HPSO iteration the particle position vector element that is related to the DG bus is examined. If it is not a positive integer value, then it is to be rounded to the nearest feasible natural number. The included rounding operator is mathematically expressed as in Eq.(25) to ensure that the HPSO bus location random choice, when initialized, is a positive integer and bounded between minimum and maximum allowable location values. |
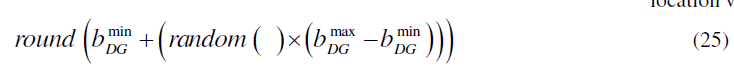 |
| During the HPSO iterations, the obtained particle position vector elements related to the DG bus locations are examined to be within limits and subsequently processed as shown in Eq. (26) to assure its distinctive characteristic, i.e. positive integer value. |
 |
| The proposed HPSO methodology is described by the flowchart shown in Figure.2. |
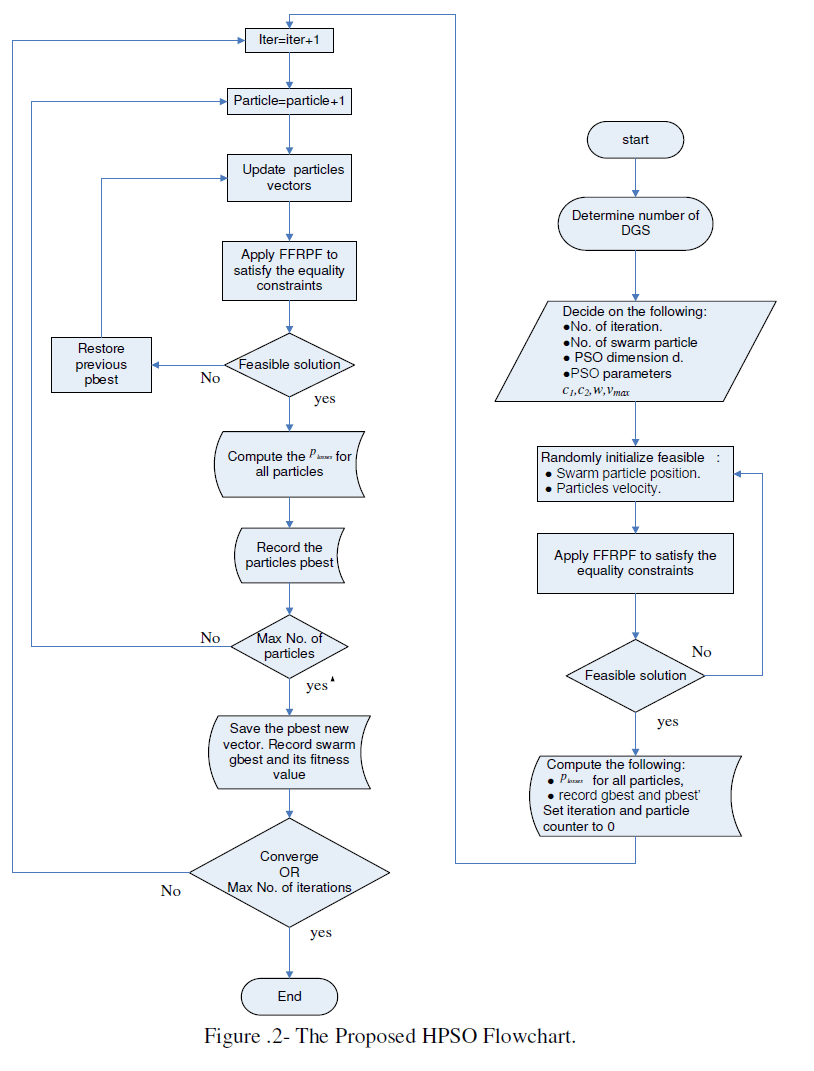 |
XI-TEST RESULTS AND DISCUSSIONS |
Introduction |
| The HPSO algorithm is used in solving the DG planning problem. The metaheuristic technique is utilized to optimally size and place the DG unit in the distribution network simultaneously, i.e. in a single HPSO run the optimal size, as both obtained for DG source. the DG unit, is optimally sized and placed in the DS network well as the bus location, are with a specified power factor ( pf ) . That is, the HPSO method is utilized in optimally placing and sizing a DG unit with a specified power factor of 0.85 . |
| Though the linear decreasing function is found to be popular in the PSO literature, the inertia weight is found to be best handled with the nonlinear decreasing function expressed in Eq. (27) |
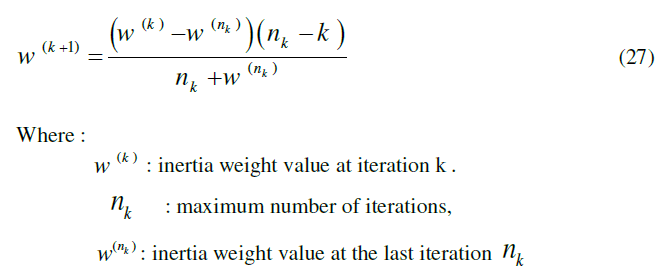 |
| . The initial and final inertia weight values, as well as the velocity minimum and maximum values are set to [0.9,0.4] and [0.1,0.9], respectively. The other HPSO parameters for both models, i.e. maximum number of iterations, No. of swarm particles and acceleration constants, are problem-dependent, and they are to be tuned for each case separately. |
XII-69-BUS RDS |
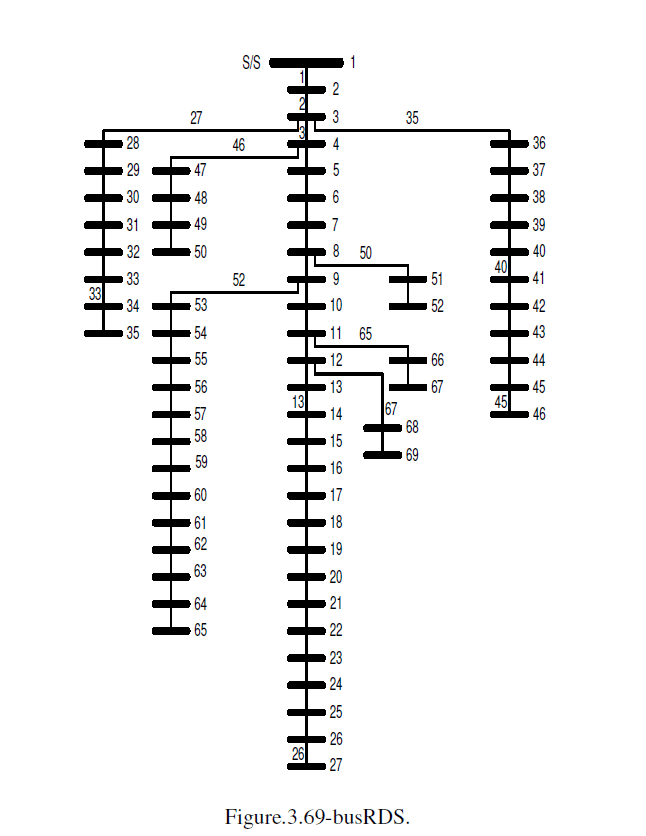
| The 69-bus RDS is the network to be tested by the proposed HPSO method, as shown in figure 3. The proposed metaheuristic method is applied to find out the optimal placement and size of a single DG unit . The DG unit planned to be installed is dealt with a fixed pf and its real power output is the variable to be optimized by the proposed HPSO. |
XIII-LOSS MINIMIZATION BY LOCATING A SINGLE DG |
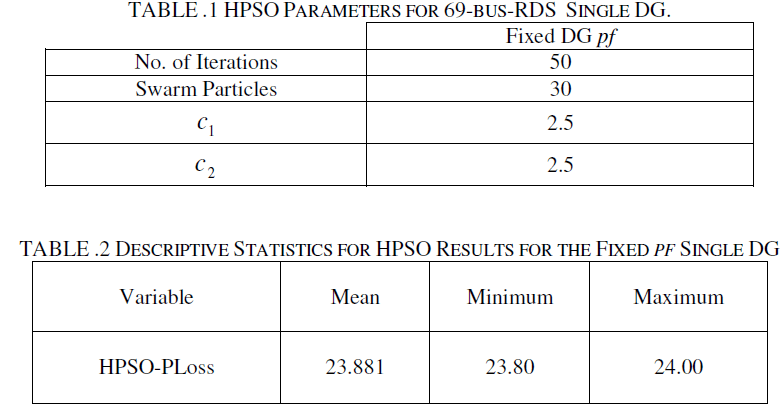
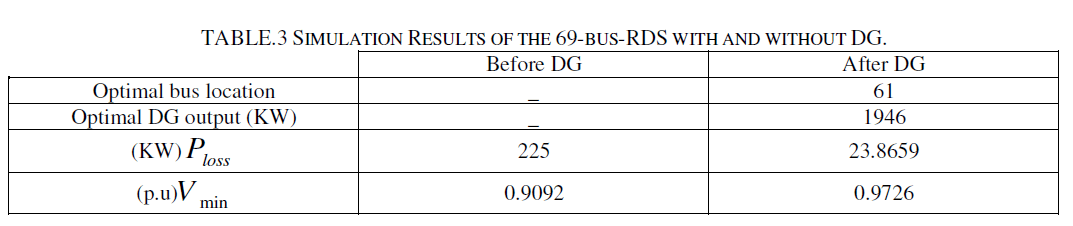
| The HPSO method was used in obtaining single DG optimal placement and size of fixed pf. Table.1 shows the tuned HPSO parameters for single DG . The HPSO simulations results consistently picked bus No. 61 for the optimal size of single DG . Their corresponding descriptive characteristics are shown in Table.2 . The proposed HPSO method obtained both the optimal bus location and the DG size that will cause the losses to be minimal simultaneously. |
 |
 |
| Table.3 shows the optimal solution of the single DG case to be installed in 69-bus-RDS. |
 |
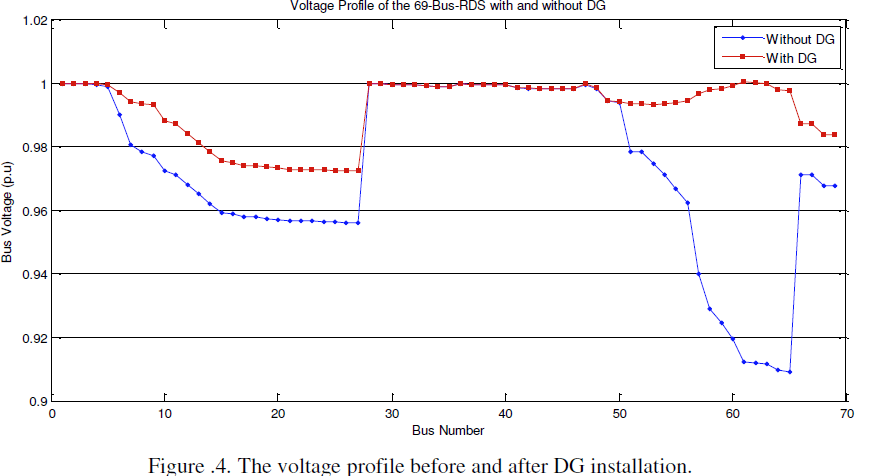
| Improving the voltage profile due to DG installation in the 69-Bus-RDS is demonstrated by Figure .4. |
 |
XIV-CONCLUSION |
| Integrating DGs in distribution systems enhance the system performance and has positive impacts such as reducing power losses and improving voltage profile. However, the benefits of DGs can only be achieved if the DG is properly installed at the optimal bus location with the optimal size. The optimal allocation and sizing of DG problem is formulated as a nonlinear mixed integer optimization problem. The objective was to find the best combination of DG location and size simultaneously while satisfying practical constraints imposed by the system planner. The DG integration problem was solved by using a relatively new optimization technique called particle swarm optimization(PSO). The PSO algorithm is a metaheuristic optimization technique which can handle objective functions of any type. The PSO was integrated with a radial power flow algorithm (FFRPF) to satisfy the equality constraints. These constraints are the nonlinear power flow equations. As for the inequality constraints, a hybrid inequality constraint handling mechanism based on preserving feasible solutions and rejecting infeasible ones where adopted in this paper. The developed PSO-based algorithm was tested on a 69-bus radial distribution system (69-Bus-RDS). The test results clearly indicate the effectiveness of the proposed technique in solving such an optimization problem. |
XV-FUTURE WORK |
| The work of this paper can be extended in several directions. The following shed some light on the possible directions in which this work can be further extended: |
| ïÃâ÷ The developed PSO-based approach can be easily employed to find the best locations and ratings of multiple DGs. |
| ïÃâ÷ The proposed PSO technique can be used to solve any other power system optimization problem such as the optimal dispatch problem. |
| ïÃâ÷ The PSO-based method can be hybridized with another optimization method in order to enhance the convergence characteristics. |
References |
|