The Significance of Integrals in Mathematics: Understanding the Heart of Calculus

About the Study

In the vast landscape of mathematics, few concepts yield as much power and versatility as the integral. Integral calculus, one of the twin pillars of calculus alongside differential calculus, plays an important role in diverse fields ranging from physics and engineering to economics and biology. The integral summarizes the idea of accumulation, enabling us to measure and analyze quantities that vary continuously. The concept of integration traces its origins back to the ancient Greeks, but it wasn't until the 17^th century that mathematicians like Isaac Newton and Gottfried Wilhelm Leibniz formalized the techniques and ideology that supports integral calculus. Integration involves the process of finding the accumulation of quantities over intervals, essentially summing up infinitesimally small pieces to determine a total.

The integral is symbolized by the elongated "S" symbol, reminiscent of the Latin word "summa," meaning sum. The integral of a function f(x) f(x) over a certain interval [a,b] [a,b] is denoted as 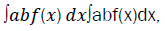where dxdx represents an infinitesimally small change in xx. Geometrically, this represents the area under the curve of f(x)f(x) between x=ab=a and x=bx=b on the Cartesian plane.

Applications across various fields

The utility of integrals extends far beyond the field of pure mathematics, permeating numerous fields and disciplines:

Physics: In physics, integrals are indispensable for calculating quantities such as displacement, velocity, acceleration, work, energy, and electric flux. For instance, the area under a velocity-time graph gives the displacement of an object, while the integral of force with respect to displacement yields the work done.

Engineering: Engineers rely on integrals for solving problems related to areas, volumes, centroids, moments of inertia, and fluid dynamics. For example, the integral of a pressure field over a surface gives the total force exerted on that surface.

Economics: In economics, integrals are used to model and analyze concepts such as total revenue, total cost, profit, consumer surplus, and producer surplus. Integrals help economists understand the behavior of markets and optimize decision-making processes.

Biology: Integrals find applications in modeling biological phenomena such as population growth, enzyme kinetics, and the spread of diseases. They enable biologists to analyze and interpret data from experiments and observations.

Profound impact and future directions

The advent of integral calculus revolutionized the way we perceive and interact with the world around us. Its applications have led to groundbreaking discoveries, technological advancements, and innovations that have shaped human civilization. From the design of bridges and buildings to the simulation of complex systems and the exploration of the cosmos, integrals serve as indispensable tools for understanding and deviating our environment.

Looking ahead, the role of integrals in mathematics and its applications is strengthened to expand further. With the advent of computational techniques and advanced algorithms, researchers are pushing the boundaries of integrals to solve increasingly complex problems and address pressing challenges in fields such as artificial intelligence, climate science, and healthcare. To conclude, integrals stand as pillars of mathematical thought, embodying the concept of accumulation and serving as a cornerstone of calculus and its applications. Their significance transcends disciplinary boundaries, making them indispensable tools for scholars, scientists, engineers, and innovators alike. As we continue to unlock the mysteries of the universe and utilize the power of mathematics to drive progress, integrals will undoubtedly remain at the forefront of our quest for knowledge and understanding.