Theoretical Foundations in Exploring the Polynomial Dynamics

About the Study

Polynomials are among the fundamental concepts in mathematics, serving as versatile tools for modeling and solving a wide range of problems across various fields. From algebraic expressions to complex equations, polynomials play an important role in both theoretical and practical applications. At its center, a polynomial is an algebraic expression consisting of variables and coefficients, combined using addition, subtraction, multiplication, and non-negative integer exponents. The general form of a polynomial is:

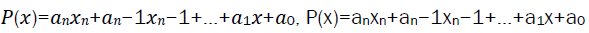
Here,xx represents the variable, a₀,a₁......a_na₀, a₁.........a_n are coefficients (constants), and nn is a non-negative integer representing the degree of the polynomial [1-3]. The highest power of the variable xx with a non-zero coefficient determines the degree of the polynomial.

Types of polynomials

Polynomials can vary in complexity and degree, leading to different classifications:

Constant polynomial: A polynomial with a degree of zero, represented by a single constant term (e.g., P(x)=5P (x)=5)

Linear polynomial: A polynomial of degree one, where the highest power of the variable is one (e.g., P(x)=2x+3P(x)=2x+3).

Quadratic polynomial: A polynomial of degree two, characterized by a squared term (e.g.,P(x)=x2+4x+1P(x)=x3+4x+1).

Cubic polynomial: A polynomial of degree three, featuring a cubed term (e.g., P(x)=3x3-2x2+x-7)P(x)=3x3−2x2+x−7).

Higher degree polynomials: Polynomials of degree greater than three, often referred to as quartic (degree four), quintic (degree five), and so on.

Properties of polynomials

Polynomials exhibit several key properties that make them essential in mathematical analysis and problem-solving:

Addition and subtraction: Polynomials can be added or subtracted by combining like terms, retaining the polynomial form [4].

Multiplication: Multiplying polynomials involves distributing each term of one polynomial across all terms of the other polynomial and then combining like terms.

Division: While division of polynomials can be more complex, techniques like long division or synthetic division enable the division of one polynomial by another.

Roots and factors: The roots of a polynomial equation are the values of the variable that make the polynomial equal to zero. Understanding these roots helps in finding factors and solving equations.

Graphical representation: Plotting the graph of a polynomial function provides insights into its behavior, including intercepts, extrema, and end behavior.

Applications of polynomials

The versatility of polynomials finds application in various fields, including:

Engineering and physics: Polynomials model physical phenomena, such as motion, electricity, and fluid dynamics, facilitating analysis and prediction.

Computer graphics: Polynomial equations are used to generate curves and surfaces in computer graphics, enabling the creation of realistic images and animations.

Economics and finance: Polynomials are employed in financial modeling, risk assessment, and optimization problems in economics and finance.

Biology and chemistry: Mathematical models based on polynomials help in understanding biological processes, chemical reactions, and population dynamics.

Signal processing: Polynomials are utilized in signal analysis, filtering, and noise reduction techniques, enhancing the quality of audio and visual signals.

Fundamentally, polynomials represent a foundation of mathematical thinking, offering a framework for understanding and solving diverse problems in mathematics and beyond [5]. Whether in algebraic manipulation, geometric analysis, or scientific modeling, the power of polynomials continues to drive innovation and discovery across disciplines, making them an indispensable tool in the toolkit of mathematicians, scientists, engineers, and researchers worldwide. Polynomials are foundational elements of mathematics with diverse applications across numerous fields. From solving equations and modeling real-world phenomena to analyzing functions and optimizing systems, polynomials empower mathematicians, scientists, engineers, and technologists to explore and understand the power of mathematics in their respective domains.

References

1. Barbeau EJ. Polynomials. Springer. 2003.

   [Google Scholar]

2. Horn Roger A, et al. Matrix Analysis. Cambridge University Press. 1990.

   [Google Scholar]

3. Kendell A. An Introduction to Numerical Analysis. John Wiley and Sons. 1988;2.

   [Google Scholar]

4. Lang S. Algebra, Graduate Texts in Mathematics. New York: Springer-Verlag. 2002;211.
5. Richard PS. Enumerative Combinatorics. Cambridge: Cambridge University Press. 1999;2.