ISSN:2321-6212
ISSN:2321-6212
Department of Physics, Beinstein College of Science, Jalukbari, Guwahati, Assam, India
Received date: 06/06/2017; Accepted date: 04/07/2017; Published date: 10/07/2017
DOI: 10.4172/2321-6212.1000176
Visit for more related articles at Research & Reviews: Journal of Material Sciences
Studies on heat conduction in nano-dimensional structures have raised numerous interests not only because of geometry dependent thermal transport but also apparently controllable heat dissipation in confined regions including the role of defects and impurity atoms. On reducing the structural size from bulk-to-nanoscale dimension, there will be significant alteration of specific heat capacity. So, thermal conductivity goes different in different temperature regimes approaching to a maximal value at 300 K for carbon nanotubes (CNTs). It may be noted that, unlike electronic contribution to the specific heat capacity, the lattice contribution in a 1D system varies as ~T (as compared to ~T3 trend for a 3D system). Though theoretically and practically thermal conductivity measurements have been carried out for SWCNT but no such theoretical works have been performed for double and triple wall carbon nanotube. We first established the theoretical calculation of thermal conductivity of DWCNT and TWCNT which matches with the experimental observations. The novelty of our work lies with the fact that we first found that as the no of walls increase in CNT from single to double to triple, thermal conductivity values decreases due to van der Waals interaction between the atoms of different walls. We see that thermal conductivity of single-wall CNT is very high (~3500 WmK-1), but it gets reduced to ~700 WmK-1 for a double-wall CNT. This drop is ascribed to incoherent heat dissipation owing significantly to the van der Waals interaction among the atoms of different co-axial walls
Carbon nanotube (CNT), Thermal transport, Carriers, Single-wall Carbon nanotube (SWCNT), Triple wall carbon nanotube (TWCNT), Multiwall carbon nanotube (MWCNT)
In the application of nano-electronics, nano-mechanics, energy storage devices, carbon nanotubes (CNTs) are viewed as the first choice by the researchers and manufacturers [1,2]. Light weight, special electronic structure, high rigidity and high thermal stability could make CNTs an ideal candidate for diverse applications of technological interest [3]. The CNTs come in the form of both single-walled tubes (SWCNTs) as well as multi-walled tubes (MWCNTs). Numerous techniques have widely been employed for synthesizing SWCNTs and MWCNTs. To name a few, are chemical vapor deposition (CVD), metal organic chemical vapor deposition (MOCVD) and other sophisticated epitaxial methods [3-5]. Although all these methods have their own advantages and disadvantages, however, in general, they are opted for obtaining large scale production of MWCNTs over SWCNTs.
In the past, CNTs have been extensively studied with regard to mechanical, thermal, optoelectronic, photovoltaic aspects. For instance, CNTs have been regularly used as cantilever tip in scanning probe microscopy, especially when, nanoscale defects and voids need to be imaged with absolute precision [6,7]. Owing to bio-conjugation capability and high specificity, the CNTs can also find value in screening and formulation of drugs with high yield. The safe interaction of CNTs with proteins and DNAs have also been demonstrated by various workers in past [8,9].
It may be worth mentioning here that, as the dimension of the devices reduces to nanometer scale, thermal management becomes increasingly important for improving circuit speed, figure of merit and overall device performance. As an important observation, the thermal conductivity of SWCNTs (~3500 WmK-1) [10] is drastically suppressed for MWCNTs. In this communication, we demonstrate heat conduction in SWCNTs and MWCNTs using modified heat diffusion model equations which consider incoherent heat dissipation but taking into account significant van der Waals interaction among the atoms of different walls.
Mathematical Analysis
The usefulness of CNTs is known for displaying exciting mechanical, electronic, thermal and optical properties while targeting on plethora of technological applications. Despite the importance of CNTs are realized in numerous fields, there has been little progress in understanding thermal conduction in CNTs especially while considering the number of walls into account. Here, by employing relevant theoretical treatments we assess thermal response of different MWCNTs with SWCNT as reference.
Single wall carbon nanotubes (SWCNT)
Ideally, CNT is the result of the rolled-up piece of a two-dimensional graphene sheet [11]. To understand the nature of thermal excitations it is important to begin with density of states of (DoS) quantized lattice vibrations (phonons). For a 2D system, the DoS of pfIG honons are given by [12]:
 (1)
(1)
Where ω and vg are the angular frequency and group velocity of phonons respectively. One can also define phonon
specific heat capacity, cs for a 2D system and is valid for 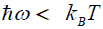 [6]
[6]
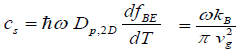 (2)
(2)
Knowing that, vg can be expressed in terms of 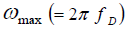 and lattice parameter
and lattice parameter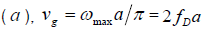 with fD as
the Debye frequency [12], we have
with fD as
the Debye frequency [12], we have
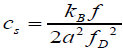 (3)
(3)
On the other hand, mean free path length (λi) of phonons, for 2D SWCNTs is represented by 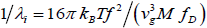 [6]. Here, M and T represent the mass of a carbon atom and the working temperature respectively. Now, we define thermal conductivity K,
for frequencies below the Debye frequency which can be formulated as [6]:
[6]. Here, M and T represent the mass of a carbon atom and the working temperature respectively. Now, we define thermal conductivity K,
for frequencies below the Debye frequency which can be formulated as [6]:
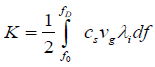
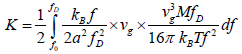
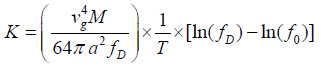 (4)
(4)
Where, 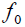 is the minimum value of arbitrary frequency (for simplicity, f0=1 Hz). Thus, in normalized form we write,
is the minimum value of arbitrary frequency (for simplicity, f0=1 Hz). Thus, in normalized form we write,
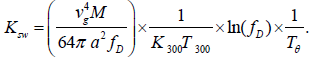 (5)
(5)
Here, 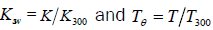 are the normalized thermal conductivity
are the normalized thermal conductivity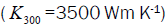 and normalized temperature
(T300=300 K) respectively.
and normalized temperature
(T300=300 K) respectively.
Double-wall carbon nanotubes (DWCNT)
As can be observed from Figure 1, thermal conductivity drops significantly with increase of number of walls. In particular, as compared to SWCNT, the K value drops by over 60% in case of a DWCNT. Typical value of thermal conductivity for DWCNT is close to 600 Wm-1K-1 [1]. While thermal conductivity of CNTs is determined by the strength of lattice vibration, the reason for a decreasing trend can be attributed to the van der Waals interaction between the carbon atoms of the adjacent walls. Such an interaction is believed to exist when the inter-wall spacing is less than 0.7 nm in accordance with the Lenard-Jones potential curve. The effective van der Waals attraction between the neighboring atoms of the adjacent walls is responsible for suppression of thermal conductivity measure along the axial direction of the CNT. In order to calculate effective frequency associated with van der Waals interaction we consider a model figure illustrated in Figure 1.
Let us consider two neighboring atoms A1 and B1 of two different walls experiencing a force, F. It may be noted that, when lattice
vibration propagate along the axial direction then all the atoms oscillate about their mean positions. The atomic displacement (x)
is considered to be small as compared to the separation between the walls (l). When A1 atom is displaced from its mean position
(position 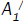 ) then the force component F sinθ would try to reduce the displacement x. Similarly, F sinθ component also acts on
the atom at B1, when it is displace from the mean position. This can be attributed to unsynchronized thermal vibration of the atoms A1 and B1. The normal component F cos θ is insignificant in this case. An expression for the reduced frequency of oscillation, ωr of atomic vibration can be predicted using Newtonian mechanics.
) then the force component F sinθ would try to reduce the displacement x. Similarly, F sinθ component also acts on
the atom at B1, when it is displace from the mean position. This can be attributed to unsynchronized thermal vibration of the atoms A1 and B1. The normal component F cos θ is insignificant in this case. An expression for the reduced frequency of oscillation, ωr of atomic vibration can be predicted using Newtonian mechanics.
Referring to Figure 1, we write,
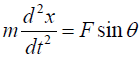 (6)
(6)
In terms of frequency,
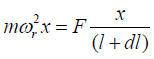
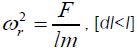
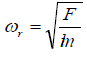 (7)
(7)
The value F can be determined from the Lenard-Jones formula:
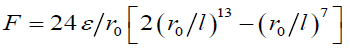 (8)
(8)
Where, 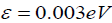 and
and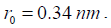
The thermal conductivity of DWCNT is believed to be suppressed by an amount that corresponds to the reduced frequency 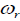 characterized by equation (7). The resultant thermal conductivity of the DWCNT can now be formulated using equation (3) as,
characterized by equation (7). The resultant thermal conductivity of the DWCNT can now be formulated using equation (3) as,
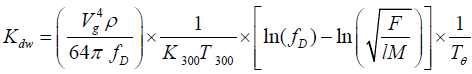 (9)
(9)
Triple-wall carbon nanotube (TWCNT)
A TWCNT is composed of three coaxial cylindrical nanotubes with wall spacing of the order of several Å. In a TWCNT, the
carbon atoms of the mid-inner wall are largely influenced by atoms of the central and outer wall. In other words, each of the inner
wall atoms is equally pulled by neighboring atoms belonging to nearby walls. Consequently, the reduced frequency corresponding
to the inner and outer walls is 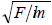 but
but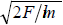 for middle wall atoms. The resultant reduced frequency responsible for the
reduction of thermal conductivity of TWCNT can be given by:
for middle wall atoms. The resultant reduced frequency responsible for the
reduction of thermal conductivity of TWCNT can be given by:
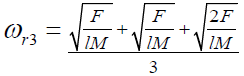 (10)
(10)
And the effective thermal conductivity for TWCNT can be stated as,
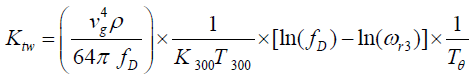 (11)
(11)
In Figure 2 Line (a) showing the graphical profile of the equation (5), how normalized thermal conductivity varies with normalized temperature. Line (b) plotted from the empirical data. We can see both Line (a) and Line (b) are almost alike. And at T0=1.4 for the both Line, thermal conductivity has the almost same value. At all temperature the value theoretical thermal conductivity is always greater than observed value. It is due to the impurity, defect on the nanotube.
Again from the Figure 3 we can see the abrupt decrease in thermal conductivity of DWCNT (n= 2) with respect to the thermal conductivity of SWCNT (n=1). We see that thermal conductivity of single-wall CNT is very high (~3500 WmK-1), but it gets reduced to ~700 WmK-1 for a double-wall CNT at room temperature [13].
From the 3D Figures 4 and 5 we can also see that thermal conductivity increase with the length of the nanotube.
From the Figure 3 it can be concluded that thermal conductivity of CNT decrease with the no of coaxial nanotubes. And it is also seen that the value of normalized thermal conductivity seem to be almost constant (w.r.t no of nanotubes) as the number nanotubes increases [14,15].
A number of experimental and theoretical investigations have been focused on the electronic structures of carbon nanotubes in order to understand the origin of their remarkable phenomena. In recent years there are many devices introducing such as CNTs solar cell, CNT superconductor, CNTs as thermoelectric device etc. which are based on thermal properties of CNTs.
Despite the importance there has been little progress in characterizing the thermal conduction in nanotube. In this work we give a new theoretical approach for calculating the thermal conductivity of DWCNT and TWCNT at different temperature. This theoretical value almost fit with the experimental value. In DWCNT and TWCNT thermal conductivity drops down sharply (with respect to the SWCNT), which will help us to calculate and stimulate this in the future for the farther research.