Thermodynamics Study on the Decay Properties of Reversed Domains in LiNbO₃ Single Crystals

Abstract

The decay properties of reversed domains fabricated by scanning probe microscopy fixed-point poling in LiNbO3 single crystals are simulated by a modified dynamic Ginzburg–Landau equation based on a simple model. The depolarization field is equivalently acted by the coercive field of ferroelectrics. The penetrated domain with a small coercive field is stable and has a long lifetime. The non-penetrated domain with maximum coercive field may ultimately experience a metastable state and disappears. Our theoretical results well agree with known experiments. We predict that the non-penetrated domain lifetime decreases with increased temperature.

Keywords

LiNbO₃, Reversed domain, Decay, Ginzburg–Landau equation, Coercive field

Introduction

Artificially ordered domain structures could be used in electro-optic modulators, and the domain switching property under external field is useful for data storage. The key for increasing the degree of miniaturization and integration density of ferroelectricbased devices is the formation of stable domains with submicron and nanometer lateral dimensions. LiNbO₃ single crystal is a ferroelectric with an ABO₃ structure and high spontaneous polarization (PS ≈ 0.75 C/m2 at room temperature) [1-3]. It occurs at the second-order phase transition from spatial group R3c (C_3v⁶) to 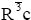(D_3d⁶) at a high Curie temperature (T_C=1484 K) [1,3-6]. Progress in the applications of scanning probe microscopy (SPM) in fabricating and exploring the micro- to nanoscale domain structures in LiNbO₃ has revealed new opportunities for the development of short-wave output and high-density storage [7-10].

Bulk LiNbO₃ crystals were poled by various voltage pulses at fixed points, and the decay process of the fabricated domains after poling was investigated by Kan et al. using SPM [9]. They found the following rules: (1) Reversed domains with an initial radius r larger than the critical initial radius rC existed beyond 5 days; rC corresponded to the point at which the domain just penetrated the crystal. (2) r_C is related to the thickness of the crystals H, that is, r_C =107 × H^0.363 . (3) Domains with an initial radius, RC<r<rC, experienced a metastable state before completely disappearing. (4) Domains smaller than the initial radius R_C switched back rapidly. (5) The dependence of domain life time on the initial radius obeyed an exponential law.

Kan et al. [9] used the Molotskii’s theory [11-14] to explain their experimental results qualitatively. The quantitative explanation, especially on the dependence of the domain lifetime on temperature, is still limited. In this paper, a simple model is proposed to investigate the decay properties of the reversed domains fabricated by SPM–fixed-points poling in LiNbO₃ single crystals. A modified dynamic Ginzburg–Landau equation is used to simulate the domain evolution. The results agree with the experimental results by Kan et al. [9].

Theoretical Development

As shown in Figure 1, the reversed domain is surrounded by a cylinder LiNbO₃ crystal with radius R (an adjustable parameter) and length H (the thickness of the crystal). The domain is assumed to have a half ellipsoid shape with semi-axes parallel (l) and perpendicular (r) to the spontaneous polarization direction [11]. After poling, the domains decay and reach a final stable state under the free energy minimum condition [12]. Following Kan [9] and Molotskii [13,14], an invariant shape was assumed to exist, i.e.,

r = Cl^1/3 (1)

Obviously, positive bond charges gather on the domain wall. The charges contributed by the reversed domain (the white region) are repulsed by the charges contributed by the unrevised region (the grey region), which induce the reversed domain decay or the growth of the unrevised region. We define polarization as to describe the growth of the unrevised region or the decay of the reversed domain. The reversed domain disappears when r=0 or P=1.

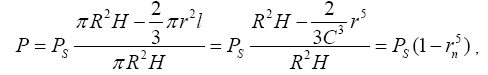(2)

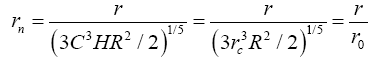(3)

Following the dynamical model that describes the hysteresis in ferroelectric ceramics presented by Guyomar et al. [15,16], the evolution of P satisfies:

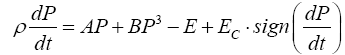
Where ρ is the electrical resistivity of LiNbO₃ single crystal and dependent on temperature T with the Arrhenius relation [17].

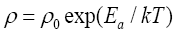(5)

Where ρ₀ is the pre-exponential factor, k is the Boltzmann constant, and E_a is the activation energy. ρ is considered a damping factor in other cases [18-20]. E is the external electric field and is zero for the reversed domain decay case discussed. E_C is the coercive field of ferroelectrics and dependent on the temperature and reversed domain length. Here, it acts equivalently to the Coulomb repulse of the bond charge on the domain wall, similar to the depolarization field in Wang’s model [17]. A and B are the coefficients of the Ginzburg–Landau–Devonshire free energy per unit volume of the LiNbO₃ single crystals [3],

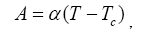
B is independent on the temperature. With E=0, let

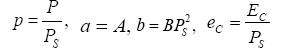(7)

Eq. (4) becomes

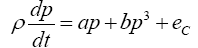(8)

and Eq. (2) becomes

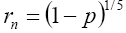(9)

Consider the steady state of eqn. (8),

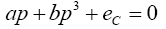
Let

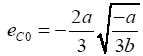
Three real roots can be derived from eqn. (10) when e_c < e_c0, two real roots when e_c= e_c0 , and one real root when e_c > e_c0. If certain small time-dependent perturbations are imposed on the system within the framework of a linear analysis [21], the perturbed state is given by:

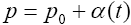
With 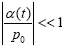. p₀ is one solution for eqn. (6). Substituting eqn. (9) into the time-dependent kinetic eqn. (10) then yields the following relation:

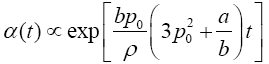
p₀ is the stable solution for eqn. (10) when 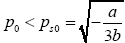. It is a non-stable solution when p₀ > p_s0 and critical stable when p₀=p_s0.

Results and Discussions

Based on eqns. (5-11) and the parameters listed in Table 1, the decay properties of the reversed domains in LiNbO₃ single crystals are calculated and discussed as follows:

Table 1. Parameters used in this work [1-3,20]

1. The Coercive Field and Stability of the Penetrated Domain

For the penetrated domain shown in Figure 1b, the Coulomb repulse of the bond charge on the domain wall is weaker than that of the non-penetrated domain shown in Figure 1a. The bigger the initial domain radius is, the more part is penetrated and the smaller is the coercive field e_c. The dependence of the normalized polarization (p > 0) on e_C at room temperature is calculated by eqn. (10) and shown in Figure 2a. A stable solution p₀₁ for one e_C<e_C0 was obtained. The time dependence of the normalized radius (r_n) for various initial values at room temperature are calculated and shown in Figure 2b. The theoretical results are qualitatively consistent with the experimental results [9].

Figure 1a: Schematic of the model used.

Figure 1b: Schematic of the penetrated domain.

Figure 2a: Dependence of the normalized polarization (p > 0) on e_C at room temperature.

Figure 2b: The time dependence of the normalized radius (rn) for various initial values at room temperature (inset: experimental results [9]).

2. Time Evolvement of the Non-Penetrated Domain

For the non-penetrated domain shown in Figure 1a, e_c= e_c0 . The solution of eqn. (10), p=p_s0, is critical stable. With ρ₀ = 1.5×10⁹ Ω⋅m, the time dependence of the normalized radius (rn) for various initial values are obtained and shown in Figure 3a. The reversed domains disappear when r_n = 0. The reversed domains with an initial normalized radius larger than 0.86 exhibit a metastable state. The result agrees with Molotskii’s conclusion obtained by dynamic theory [14]. The reversed domain exits a few seconds when its initial normalized radius is smaller than 0.6. The domain with intermediate radius keeps the period of time. The decay characteristic of the reversed domain originates from the nonlinear property of the LiNbO₃ crystals and is independent on the thickness. With r₀=572 nm (R=510 nm), the time dependence of the normalized radius at room temperature are plotted, as shown in Figure 3b. The theoretical results well agree with the experimental results by Kan [9].

Figure 3a: The time dependence of the normalized polarization for various initial values at room temperature.

Figure 3b: The time dependence of the normalized radius at room temperature (solid points: experimental results; solid line: theoretical results).

3. Dependence of the Domain Lifetime on the Initial Domain Radius and Temperature for Non-Penetrated Domain

With ρ₀ = 1.5×10⁹ Ω⋅m and r₀=572 nm (R=510 nm), the dependence of the domain lifetime on the initial domain radius for H=88 μm is plotted, as shown in Figure 4a. The parameters a and e_C in eqn. (8) are temperature dependent; hence, the domain lifetime on the temperature can be predicted for initial domain radius 500 nm, as shown in Figure 4b. The domain lifetime decreases rapidly as the temperature increases. Obviously, thermal motion intensifies the domain decay. On one hand, increased temperature gives rise to the high nonlinearity in eqn. (8). On the other hand, increased temperature reduces the electrical resistivity.

Figure 4a: Dependence of the domain lifetime on initial domain radius.

Figure 4b: Dependence of the domain lifetime on the temperature.

Conclusions

A modified dynamic Ginzburg–Landau equation is used to simulate the decay properties of the reversed domains fabricated by SPM–fixed-points poling in LiNbO₃ single crystals. The penetrated domain has a very long lifetime. The domain lifetime increases as the initial domain radius increases for the non-penetrated domain. The theoretical results well explain the experimental results. The Coulomb repulse of the bond charge on the domain wall may be equivalent to the coercive field of ferroelectrics. The domain lifetime decreases as the temperature increases.

References

1. Zhang MS. The ferroelectric mixture phase transition in lithium tantalite and lithium niobate. Progr Nat Sci 1991;6:487-492.
2. Chen FS, et al. Dielectric and ferroelectric properties of Sodium-Lithium niobate crystals. J Shandong Univ 1985;2:69-75.
3. Kim S, et al. Coercive fields in ferroelectrics: A case study in lithium niobate and lithium tantalite. Appl Phys Lett 2002;80:2740-2742.
4. Abrahams SC, et al. Ferroelectric lithium niobate. 4. Single crystal neutron diffraction study at 24°C. J Phys Chem Solids 1966;27:1013-1018.
5. Abrahams SC, et al. Ferroelectric lithium tantalate—III. Temperature dependence of the structure in the ferroelectric phase and the para-electric structure at 940°K. J Phys Chem Solids 1973;34:521.
6. Johnston WD and Kaminov IP. Temperature Dependence of Raman and Rayleigh Scattering in LiNbO3 and LiTaO3. Phys Rev 1968;168:1045.
7. Rodriguez BJ, et al. Domain growth kinetics in lithium niobate single crystals studied by piezoresponse force microscopy. Appl Phys Lett 2005;86:012906.
8. Kan Y, et al. Growth evolution and decay properties of the abnormally switched domain in LiNbO3 crystals. Appl Phys Lett 2008;92:172910.
9. Kan Y, et al. Critical radii of ferroelectric domains for different decay processes in LiNbO3 crystals. Appl Phys Lett 2007;91:132902.
10. Kan Y, et al. Domain reversal and relaxation in LiNbO3 single crystals studied by piezoresponse force microscope. Appl Phys Lett 2006;89:262907.
11. Landauer R. Electrostatic consideration in BaTiO3 domain formation during polarization reversal. J Appl Phys 1957;28:227.
12. Molotskii M, et al. Ferroelectric Domain Breakdown. Phys Rev Lett 2003;90:107601.
13. Molotskii M. Generation of ferroelectric domains in atomic force microscope. J Appl Phys 2003;93:6234.
14. Molotskii M and Shvebelman MM. Decay of ferroelectric domains formed in the field of an atomic force microscope. J Appl Phys 2005;97:084111.
15. Guyomar D, et al. Dynamical hysteresis model of ferroelectric ceramics under electric field using fractional derivatives, J Phys D: Appl Physic 2007;40:6048-6054.
16. Guyomar D, et al.Time fractional derivatives for voltage creep in ferroelectric materials: theory and exoeriment. J Phys D: Appl Physic 2008;41:125410.
17. Bhatt R, et al. Optical bandgap and electrical conductivity studies on near stoichiometric LiNbO3 crystals prepared by VTE process. J Phys Chem Solids 2012;73:257-261.
18. Wang B and Xia R, Fan H, Woo CH, Dynamic process of domain switching in ferroelectric films, J. Appl. Phys. 2003;94:3384-3389.
19. Bandyopadhyay AK, et al. Dynamical systems analysis for polarization in ferroelectrics. J Appl Phys 2006;100:114106.
20. Cao WW, et al. Simulation of boundary condition influence in a second-order ferroelectric phase transition. J Appl Phys 1999;86:5739-5746.
21. Lefever R, et al. On the Occurrence of Oscillations around the Steady State in Systems of Chemical Reactions far from Equilibrium. J Chem Phys 1967;47:1045-1047.