Towards a Precise Formula for Counting Prime Numbers

Abstract

This paper delves into the possibility of creating a precise mathematical equation to calculate the exact number of prime numbers below a certain threshold. By utilizing tools from function analysis, series of functions, and innovative methods, the goal is to create a comprehensive formula that can accurately determine the quantity of primes within a specified numerical range. The research explores the theoretical underpinnings of prime numbers, using advanced techniques to improve and expand upon current methodologies. Through a combination of insights from function analysis and series theory, the proposed formula seeks to offer a strong and efficient solution for computing prime counts. This effort not only adds value to the field, but it also enhances our understanding of prime number distribution.

Keywords

Counting; Distribution; Solution; Prime numbers; Function analysis

Introduction

In the realm of number theory, the quest to count prime numbers has been a longstanding and fundamental challenge. The identification and enumeration of primes, those elusive integers divisible only by 1 and themselves, have intrigued mathematicians for centuries. The prime counting function, denoted as π(x), represents the number of primes less than or equal to a given positive integer x.

This paper embarks on a journey to explore the possibility of formulating a precise and efficient method for calculating the exact number of prime numbers less than a given threshold. Our approach hinges on the utilization of various tools in the analysis of functions, series operations, and the introduction of innovative techniques to advance the understanding of prime distribution.

Central to our development is the exploration of a serial tool known as “divisor,” a unique series operator of divisions. This operator serves as a pivotal component in our investigation, and its intricacies will be unraveled to pave the way for a deeper comprehension of prime number patterns.

As we delve into the intricacies of the divisor series operator, we aim to establish a foundation for a comprehensive formula that accurately counts prime numbers. By integrating tools from function analysis, series operations, and introducing novel methodologies, we endeavor to contribute to the ongoing dialogue surrounding prime number theory.

In the subsequent sections, we will dissect the divisor series operator, laying the groundwork for its incorporation into a broader framework for prime counting. Through this exploration, we aspire to offer fresh insights into the realm of prime number theory and present a promising avenue for the development of a precise prime counting formula. [1-5]

Description

Theorem

The division operation can be translated into a serial operator with D notation, it has some different variations of notation,

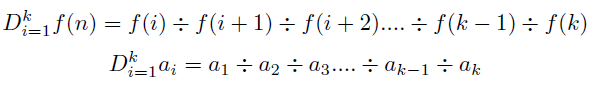
The divisory of sets

Theorem: We can use the tool of divisory but instead a variable we introduce a constant, we should apply one to one division operations to obtain a set as result.

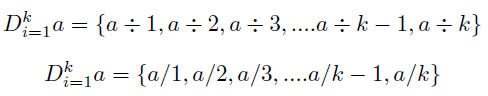
For example, if you do the set divisor of 3 at all range, you will get the following set.

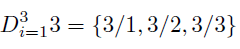
Definition of our f(x) function

We define our f(x) function as 1 if in the process of analyze the set we have, r=2 and we define f(x) function a 0 if we have r<2 or r>2. Where s is the number of natural numbers.

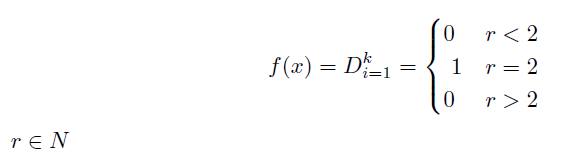
Example 1

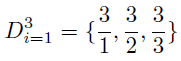
f(x)=1 because there are 2 natural numbers.

Example 2

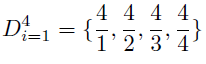
f(x)=0 because there are 3 natural numbers r=3>2.

Theorem

A prime number always give an f(x)=1 and a composite number always give an f(x)=0. A formula for the number of prime numbers less than a given number.

Theorem: The formula for the exact number of prime less than a given number implies a summation for the accumulation of the results and a set serial division which gives us the partial results, and it is the next formula.

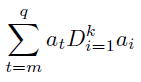
The variable q is a hypothetical result as maximum of the summation, the result of number of primes will always less than q.

Example 1

For example, the number of primes less than 4 are given by

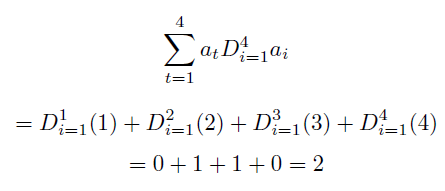
Example 2

For example, the number of primes less than are equal 4 given by

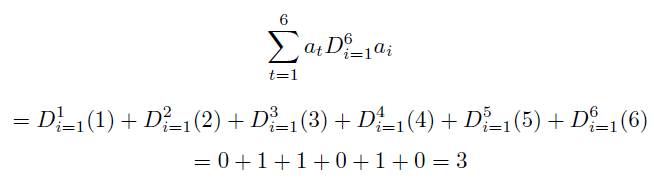
Example 3

For example, the number of primes less than are equal 8 given by

Conclusion

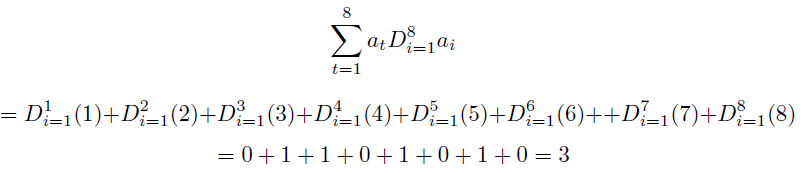
When it comes to math and number theory, deciding between approximations and accurate methods depends on finding the right balance between precision and computational efficiency. While accurate methods give exact solutions, they can be costly in terms of computation, especially for large-scale problems. On the other hand, approximation methods are quicker but may lack some precision. The best approach varies based on the problem at hand, resources available, and desired level of accuracy. For formulas that are exact but cumbersome to compute, it’s important to explore optimization strategies for practical use in real-world situations.

References

1. Zaman BU. Natural number infinite formula and the nexus of fundamental scientific issues. TechRxiv. 2023;1-19.

   [Crossref] [Google Scholar]

2. Zaman BU. New prime number theory. TechRxiv, Authorea. 2023.

   [Crossref] [Google Scholar]

3. Zaman BU. The Philosophical and Mathematical Implications of Division by 0/0=1 in Light of Einstein�??s Theory of Special Relativity. 2023.

   [Google Scholar]

4. Zaman BU. Prime discovery a formula generating primes and their composites. TechRxiv, Authorea. 2023.

   [Google Scholar]

5. Zaman BU. Every prime number greater than three has finitely many prime friends. Technical report, EasyChair, 2024.

   [Google Scholar]