Research & Reviews: Journal of Engineering and Technology
MenuISSN: 2319-9873
ISSN: 2319-9873
+44 7456 035580 Radhika Katkum1,2*, Harish Kalla3, Arun Roy Vadde3, Rama Krishna T1
1Department of Computer Science and Engineering, Jayamukhi Institute of Technological Sciences, Narsampet, Warangal - 506 332, India.
2Department of Physics and Computer Science, Vaagdevi Group of Colleges, Hanamkonda, Warangal -506001, India.
3Department of Electrical & Computer Engineering, School of Engineering and Technology, Wollega University, Post Box No: 395, Nekemte, Ethiopia
Received: 02 May 2014 Accepted: 28 May 2014
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
A transaction database usually consists of a set of time-stamped transactions. Mining frequent patterns in transaction databases has been studied extensively in data mining research. However, most of existing frequent pattern mining algorithms does not consider the time stamps associated with transactions. We extended the existing frequent pattern mining framework to take into account the time stamp of each transaction and discover patterns whose frequency dramatically changes over time. We define a new type of patterns, called Transitional Patterns, to capture the dynamic behavior of frequent patterns in a transaction database. Transitional patterns include both positive and negative transitional patterns. Their frequencies increase or decrease dramatically at some time points of a transaction database. We introduced the concept of significant milestones for a transitional pattern, which are time points at which the frequency of the pattern changes most significantly. Moreover, we developed an algorithm to mine the set of transitional patterns along with their significant milestones from the transaction database
Algorithm, Dynamic behavior, Frequent patterns, Mining research, Transaction database.
In the present study, the authors extending the traditional frequent pattern mining framework to take into account the timestamp of each transaction, i.e., the time when the transaction occurs. Also tried to define a new type of patterns, called transitional patterns, to represent patterns whose frequency dramatically changes over time [1,2]. Transitional patterns include both positive and negative transitional patterns. The frequency of a positive transitional pattern increases dramatically at some time point of a transaction database, while that of a negative transitional pattern decreases dramatically at some point of time [3,4].
The mining of frequent item sets is to find all the item sets from a transaction database that satisfy a user-specified support threshold. It is one of the fundamental and essential operations in many data mining tasks, such as association rule mining, sequential pattern mining, structured pattern mining, correlation mining and association classification [5]. Since it was first introduced by Agrawal et al in 1993, the problem of frequent item set mining has been studied extensively [6]. As a result, a large number of algorithms have been developed in order to efficiently solve the problem, including the most well-known Apriori, FP-growth and Eclat algorithms. The number of frequent patterns generated from a data set are often excessively large, and most of them or useless or simply redundant. Thus, there has been interest in discovering new types of patterns including maximal frequent item sets, closed frequent item sets, indirect associations and emerging patterns. Mining for maximal or closed frequent item sets greatly reduces the number of generated patterns by generating only the largest frequent item sets with no frequent superset or no superset of higher frequency. A common characteristic of the above learning methods is that they treat the transactions in a database equally and do not consider the time points at which those transactions occurred. Therefore, the existing algorithms can reveal the static behavior of the frequent patterns. The frequency of the patterns which changes over the time period is called dynamic behavior of the patterns. To capture the dynamic behavior of the patterns, new type of patterns were introduced, called Transitional Patterns [7,8].
Preliminaries
In data mining applications, to extract the interesting patterns from databases, mining frequent patterns is one of the fundamental operations. Let I= {i1, i2 … in} be a set of items. Let D be a set of database transactions where each transaction T is a set of items and ||D|| be the number of transactions in D. Given X= {ij … ik} ⊆ I (j ≤k and 1 ≤ j, k ≤ n) is called a pattern. The support of a pattern X in D is the number of transactions in D that contains X. Pattern X will be called frequent if its support is no less than a user specified minimum support threshold [7].
Definitions
Definition 1(Cover): The cover of an item set X in D, denoted by cov(X,D), is the number of transactions in which the item X appears.
Definition 2(Support): An item set X in a transaction database D has a support, denoted by sup(X, D), which is the ratio between cov(X, D) to the number of transactions in D i.e.,||D||.
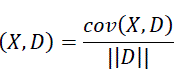
Definition 3 (Position of a transaction): Assuming that the transactions in a transaction database D are ordered by their time-stamps, the position of a transaction T in D, denoted by ρ(T), is the number of transactions whose time-stamp is less than or equal to that of T. Thus 1≤ ρ(T) ≤ ||D||.
Definition 4: The ith transaction of a pattern X in D, denoted by Ti(X), is the ith transaction in cov(X) with transactions ordered by their positions, where 1≤ i ≤ cov(X, D).
Definition 5 (ith milestone): The ith milestone of a pattern X in D, denoted by ξi(X), is defined as
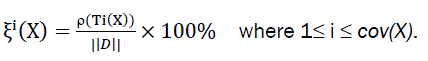
Definition 6: The support of the pattern X before its ith milestone in D, denoted by supi_(X) is defined as
Definition 7: The support of the pattern X after its ith milestone in D, denoted by supi_(X ) is defined as
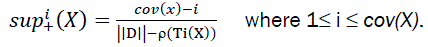
Definition 8 (Transitional Ratio): Transitional ratio is used to measure the difference of a pattern’s frequency before and after its ith mile stone. The Transitional ratio of the pattern X at its ithmile stone in D is defined as
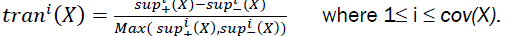
It is easy to see that the higher the absolute transitional ratio of a pattern at its ith milestone, the greater the difference between its supports before and after its ithmilestone. A nice feature of this definition is that the value of a transitional ratio is between _1 and 1. As for transitional patterns, I am interested in patterns whose absolute values of transitional ratio are large, which are defined below.
Definition 9 (Transitional Pattern): A pattern X is a transitional pattern (TP) in D if there exists at least one milestone of X, ξk(X) ∈Tξ, such that:
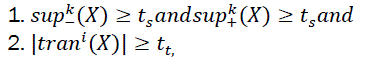
Where Tξis a range of ξi(X) (1≤ i ≤ cov(X)), ts and tt are called pattern support threshold and transitional pattern threshold, respectively. X is called a Positive Transitional Pattern (PTP) when tran (X )>0; and X is called a Negative Transitional Pattern (NTP) when trank(x )<0.
Definition 10 (Significant Frequency-Ascending Milestone) :The significant frequency-ascending milestone of a positive transitional pattern X with respect to a time period Tξ is defined as a tuple, (ξM(X),tranM(X)), where ξM(X)∈Tξis the Mth milestone of X such that
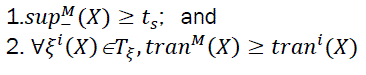
Definition 11 (Significant frequency-descending milestone): The significant frequency-descending milestone of a negative transitional pattern X with respect to a time period Tξ is defined as a tuple, (ξN(X),tranN(X)), where ξN(X)∈Tξis the Nth milestone of X such that
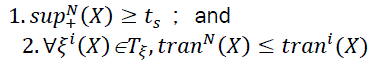
Designing
This part of the paper presented the design aspects of system and an algorithm, called TP-mine, for mining the set of positive and negative transitional patterns and their significant milestones with respect to a pattern support threshold and a transitional pattern threshold. The algorithm is given as data flow diagram, which is a graphic tool. It is used to describe and analyze the movement of data through a system-manual or automated. They focus on the data flowing in to the system, between process and in and out of data stores. This is a central tool and the basis from which other components are developed1, 6. Figure 1 explains the context level diagram, Figure 2 showed collaboration diagram and the Figure 3 explains the total activity chart.
TP-Mine Algorithm
TP-mine. (Mine the set of Transitional Patterns and their significant milestones)
Input: A transaction database (D), an appropriate milestone range that the user is interested (Tξ), pattern support threshold (ts), and transitional pattern threshold (tt).
Output: The set of transitional patterns (SPTP and SNTP) with their significant milestones [1].
There are two major phases in this algorithm. During the first phase (Step 1), all frequent item sets along with their supports are initially derived using a standard frequent pattern generation algorithm, such as Apriorior FP-growth, with ts as the minimum support threshold. In the second phase (starting from Step 2 to theend), the algorithm finds all the transitional patterns and their significant milestones based on the set of frequent item sets. As mentioned before, a pattern that is frequent before and after one of its milestones in D with respect to support threshold ts must be frequent on D with respect to the same threshold. Thus, it is safe for us to first mine the frequent item sets on the entire database using the threshold ts, and then find the transitional patterns based on the set of frequent item sets.
In Step 2, the support counts of all the frequent patterns on the set from the first transaction to the transaction right before the time period Tξ are collected. They are used later in computing sup_ck(Pk), where Pi is a frequent pattern. Step 3initializes the set of positive transitional patterns (SPTP) and the set of negative transitional patterns (SNTP) to empty.
Steps 4-7 initialize the set of significant frequency-ascending milestones for each frequent pattern Pk, SFAM (Pk), and the set of significant frequency-descending milestones for each frequent pattern Pk, SFDM (Pk), to empty. It also initializes the maximal and minimal transitional ratios of Pk, denoted by MaxTran (Pk) and MinTran (Pk), to zero. After the initializations, the algorithm continues to scanthe database D to find the milestones of Pk within the range Tξ. At each valid milestone ξck(Pk) during the scan, it calculates the support of Pk before ξck(Pk), i.e., sup_ck(Pk ) and the support of Pk after ξck(Pk), i.e., sup_ck(Pk)(Pk ), If both of them are greater than ts, the algorithm then checks the transitional ratio of Pk. If the ratio is greater than tt, then Pk is a positive transitional pattern and is added into the set SPTP. Then, the algorithm checks whether the transitional ratio of Pk is greater than the current maximal transitional ratio of Pk. If yes, the set of significant frequency-ascending milestones of Pk, i.e., SFAM (Pk), is set to contain {ξck(Pktranck(pk) as its single element. If not but it is equal to the current maximal transitional ratio of Pk, (Pk ) (Pk ) is added into SFAM (Pk).Similarly, Steps 23-32 are for finding the set of negative transitional patterns and their significant frequency-descending milestones.
To demonstrate the efficiency of the TP-Mine algorithm we have done experiments on synthetic data obtained shown in Table 1. The results were shown in Table 2 and explained through Figures 4, 5 and 6. Our experimental results showed that the proposed algorithm is highly efficient and scalable.
Table 1: Example Database
Table 2: Some of the milestones and transitional patterns
Figure 1: Context level diagram
Figure 2: Collaboration diagram
Figure 3: Activity diagram
Figure 4: Transitional ratios in TDB
Figure 5: Frequent patterns with their supports
Figure 6: Transitional patterns and their milestones
A limitation of existing frequent item set mining framework is that it does not consider the time stamps associated with the transactions in the database. As a result, dynamic behavior of frequent item sets cannot be discovered. In this study, we introduced a novel type of patterns, positive and negative transitional patterns, to represent frequent patterns whose frequency of occurrences changes significantly at some points of time in a transaction database. And also defined the concepts of significant frequency-ascending mile stones and significant frequency-descending milestones to capture the time points at which the frequency of patterns changes most significantly. To discover transitional patterns, proposed the TP-mine algorithm to mine the set of positive and negative transitional patterns with respect to a pattern support threshold and a transitional pattern threshold. This algorithm takes one database scan after mining frequent patterns to find the transitional patterns and their significant milestones. Experimental results showed that the proposed algorithm is highly scalable. The experimental study demonstrated the use fullness of transitional patterns in two real-world domains and showed that what is revealed by the transitional patterns and their significant milestones would not be found by the standard frequent pattern mining framework.