ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
D.Mercy1, S.M.Girirajkumar2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This paper deals with the tuning of controllers for complex nonlinear process like conical tank process. Control of conical tank presents a challenging problem due to its non-linear behaviour and constantly changing cross section area. The non-linear behaviour can be overcome by applying different controlling techniques. The proposed control strategy includes the tuning of PID controller using Z-N method and intelligent techniques like Genetic Algorithm. Genetic Algorithm offers optimized solution for various complex non linear processes. Comparing with other conventional techniques the intelligent techniques provide better results in terms of high stability, robust and reliable.
Keywords |
| PID Controller, Z-N method, Non-linear control, Genetic Algorithm. |
INTRODUCTION |
| Liquid level control systems mainly control the manipulated parameter of liquid level, which in industry have a wide range of applications in various fields. In the industrial production process, there are many places need to control the liquid level, and make the liquid level maintain accurately for a given value. The traditional method is to use classical PID method. However, the practical application of the output is uncertain, in order to input well to follow the changes of output, then we need a continuously detect the number in time, to realize the liquid precise control. To implement a PID controller, three parameters (the proportional gain, Kp; the integral gain, Ki; the derivative gain, Kd) must be determined carefully. Many approaches have been developed to determine PID controller parameters for single input single output (SISO) systems. Among the well-known approaches is the Ziegler-Nichols (Z-N) method, the Cohen- Coon method, integral of squared time weighted error rule (ISE), integral of absolute error rule (IAE), internal-model control (IMC) based method, integral time squared error (ITSE), integral time absolute error (ITAE). Several new methods from an artificial intelligent approach, such as GA, PSO, ANN and fuzzy logic, the applications of GA and PSO have expanded into various fields. With the abilities for global optimization and good robustness, and without knowing anything about the underlying mathematics, GA and PSO are expected to overcome the weakness of traditional PID tuning techniques and to be more acceptable for industrial practice [1]. |
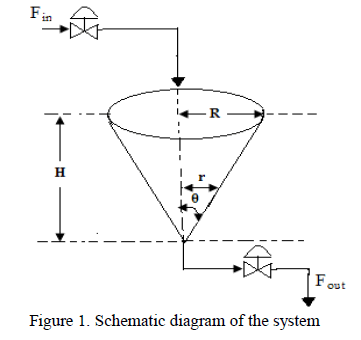
| Conical tanks are mostly used in various process industries, such as metallurgical industries, food processing industries, concrete mixing industries and wastewater treatment industries. A conical tank is basically a nonlinear process due to the change in the area of cross section and the level system with change in shape. Conventional controllers are commonly used in process industries as they are simple, robust and familiar to the field operator. Real time systems are not precisely linear but may be represented as linearized models around a nominal operating point. The controller parameters tuned at that operating point may not reflect the real-time system characteristics due to variations in the process parameters. The variations in the process parameters can be overcome by continuous adjustment of the controller parameters using intelligent techniques like Genetic Algorithm [8]. |
MODELING OF THE TANK |
| A mathematical model is a description of a process using mathematical concepts. The process of developing a mathematical model is termed as mathematical modeling. Mathematical modeling is used to explain the identified system and to study the effects of different components, and to make predictions about the process behavior. Mathematical models can take many forms, including but not limited to dynamical systems, statistical models, differential equations, etc. In this paper the proposed system includes the conical tank process whose area is variable throughout the height. |
| The mathematical model of the conical tank is determined by the following assumptions. |
| Level as the control variable |
| Inflow to the tank as the manipulated variable. This can be achieved by controlling the input flow of the conical tank. |
| Inflow rate of the tank (Fin) is regulated using the valve and the input flow through the conical tank .At each height of the conical tank the radius may vary. This is due to the shape of the tank. The difference between the inflow and the out flow rate will be based on the cross section area of the tank and level of the tank with respect to time. The flow and the level of the tank can be regulated by proper modelling the tank. |
| Operating Parameters are, |
| Fin - Inflow rate of the tank |
| Fout - Outflow rate of the tank |
| H - Total height of the conical tank. |
| R - Top radius of the conical tank |
| h - Nominal level of the tank |
| r - Radius at nominal level |
| Mass balance Equation is given by |
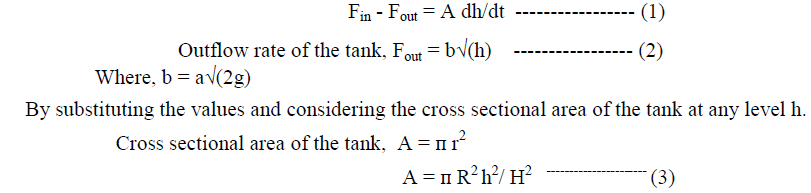 |
| Where radius, r = (Top radius of the conical tank)2(Nominal level of the tank)2 /(Total height of the conical tank)2 Therefore, r = R2h2/H2 |
 |
| Mathematical model of the conical tank is described by the set of differential equations. The differential equations describe the process with respect to time (i.e) in time domain. Transfer function of the system can obtain by converting the process from time domain to frequency domain. Transfer function of the conical tank is given by taking the partial differentiation of the linearized equation and its corresponding Laplace transform, |
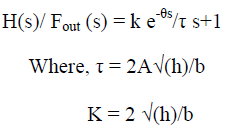 |
| The transfer function is FOPTD process and the appropriate tuning technique is used to stabilize the system. Based on the specification the transfer function is given by |
PID TUNING |
| A. PID Controllers:- |
| PID stands for Proportional-Integral-Derivative controller. The individual P, I, D terms compose the standard three-term controller. The Three-term PID controllers are widely used in various process industries. Even complex industrial control systems make the use of a control network whose main control building block is a PID controller. The three-term PID controller has survived the changes of technology from the analog era into the digital computer control system age in a satisfactory way. It was the primary controller to be produced as a mass for the high market volume that existed in the process industries. PID controller is as type of feedback controller whose output, a control variable (CV), is generally based on the error (e) between some user defined set-point (SP) and some measured process variable (PV). Each element of the PID controller refers to a particular action to be taken on the error. |
Proportional Controller: |
| In this controller error value is multiplied by a gain, Kp. This is also called as adjustable amplifier. In most of the systems Kp is responsible for process stability. If the process stability is very low then PV can drift away and if it is very high then PV starts to oscillate. |
Integral Controller: |
| The integral error is multiplied by a gain Ki. In many systems Ki is responsible for driving error to zero, but went Ki is very high is to invite oscillation or instability or integrator windup or actuator saturation. |
Derivative Controller: |
| The rate of change of error multiplied by a gain, Kd. In many systems Kd is responsible for system response: too high and the PV will oscillate; too low the PV will respond sluggishly. The designer should also note that derivative action amplifies any noise in the error signal [7]. |
B. Tuning Methods:- |
| Tuning of a PID involves the adjustment of Kp, Ki and Kd to achieve some user-defined „optimalâÃâ¬ÃŸ character of a system response. |
Z-N Method |
| Controller standardization may be a method of adjusting the management parameters like proportional gain, integral gain and spinoff gain. Controller standardization is required to urge the required management response. Generally stability of response is required and the process must not oscillate for any combination of process conditions and set points. There are various PID tuning methods are available. Among these methods Z-N method performs well. This traditional method, also known as the closed-loop method (or) on-line tuning method was proposed by Ziegler and Nichols. |
| Like all the other tuning methods, Z-N Method consists of two steps: |
| Determination of the dynamic characteristics of the control loop. |
| Estimation of the controller tuning parameters that produce a desired response for the dynamic characteristic determined in the first step, in other words, matching the characteristics of the controller to that of the other elements in the loop. |
| The tuning formula for Z-N method is shown in table.1. |
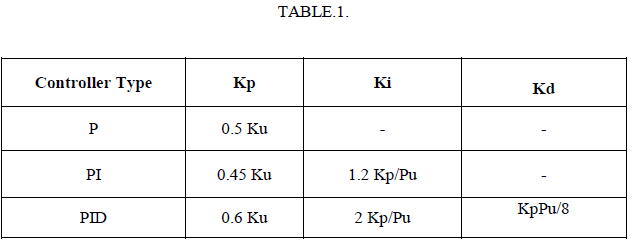 |
| The Z-N method is more robust because it does not require a specific process model. To tune a controller using the Z-N method the integral and derivative elements of the PID controller are ignored. The proportional element is used to find a Kc that will sustain oscillation. This value is considered as Ku, or the ultimate gain. The period of oscillation is the Pu, or ultimate period [25]. |
INTELIGENT TECHNIQUES |
A. Introduction to Genetic Algorithm:- |
| Genetic algorithm is one of the global search technique used for the optimization process. It mimics the process of natural evaluation. Genetic algorithms are inspired by Darwin's theory about evolution. Solution to a problem is solved by genetic algorithms. Genetic Algorithm is started with a set of solutions called population. Solutions from one population are taken and used to form a new population. This is motivated by a hope, that the new population will be better than the old one. Solutions which are selected to form new solutions are selected according to their fitness. The more suitable they are the more chances they have to reproduce. This is repeated until some condition is satisfied. |
| Genetic algorithm represents an intelligent exploitation of a random search used to solve optimization problems. Although randomized, GAs are by no means random, instead they exploit historical information to direct the search into the region of better performance within the search space. The basic techniques of the GAs are designed to simulate processes in natural systems necessary for evolution; especially those follow the principles first laid down by Charles Darwin of "survival of the fittest". Since in nature, competition among individuals for scanty resources results in the fittest individuals dominating over the weaker ones. GA is better than conventional AI in that it is more robust. Unlike older AI systems, they do not break easily even if the inputs changed slightly, or in the presence of reasonable noise. Also, in searching a large state-space, multi-modal state-space, or n-dimensional surface, a genetic algorithm may offer significant benefits over more typical search of optimization techniques [13]. |
B. Implementation Details |
| Genetic algorithms were implemented through 3 operators:` |
| Selection that equates to survival of the fittest. |
| Crossover which represents mating between individuals. |
| Mutation which introduces random modifications. |
| Selection Operator |
| Key idea: offer preference to raised people, permitting them to die their genes to ensuing generation. |
| The goodness of every individual depends on its fitness. |
| Fitness could also be determined by AN objective perform or by a subjective judgment. |
| Crossover Operator |
| Prime distinguished issue of GA from different improvement techniques. |
| Two people are chosen from the population mistreatment the choice operator. |
| A crossover web site on the bit strings is haphazardly chosen. |
| The values of two strings are changed up to the current purpose If S1=000000 and s2=111111 and therefore the crossover purpose is 2 then S1\'=110000 and s2\'=001111. |
| The two new offspring created from this mating are put into the next generation of the population by recombining portions of good individuals, this process is likely to create even better individuals. |
| Mutation Operator |
| With some low chance, a little of the new people can have a number of their bits flipped. |
| Its purpose is to keep up diversity inside the population and inhibit premature convergence. |
| Mutation alone induces a stochastic process through the search house. |
| Mutation and choice (without crossover) produce parallel, noise-tolerant, hill-climbing algorithms. |
C. Flow chart for GA process |
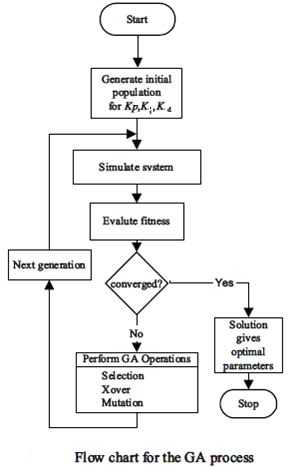 |
| The flow chart represents the stepwise procedure for finding the optimal solution for a complex process. The GA process is started with initialization of population for Kp,Ki & Kd. The fitness of the population is determined by using selection, crossover and mutation operators. If the fitness is converged the optimized solution is provided. If the fitness is not converged the GA operations will be repeated to create the next generation. |
EXPERIMENTAL SETUP |
| The Experimental set up shown in figure consists of a conical tank, a water reservoir, centrifugal pump, rotameter and an electro pneumatic converter (I/P converter). The supply for this I/P converter are provided externally. In this setup, a personal computer (PC) loaded with the MATLAB software allows the user to monitor and control the working process. |
 |
System Specification |
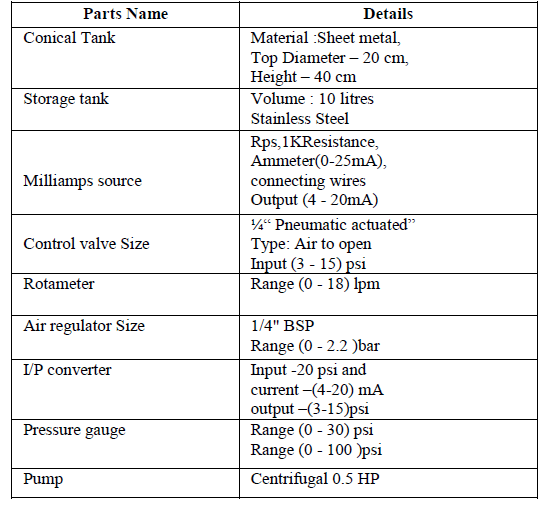 |
RESULTS & DISCUSSIONS |
A. Tuning Parameters |
| The conical tank process includes the conventional controller and is tuned using traditional tuning method like Z-N method. The tuned results are compared with the intelligent tuning techniques like Genetic Algorithm. The tuned parameters were analysed and the response curves were plotted .The controller tuning values are tabulated in table.2. |
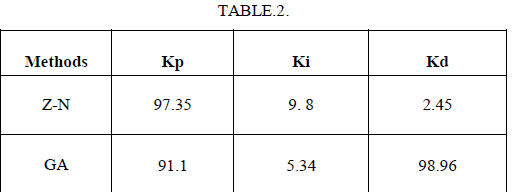 |
B. Response Curve |
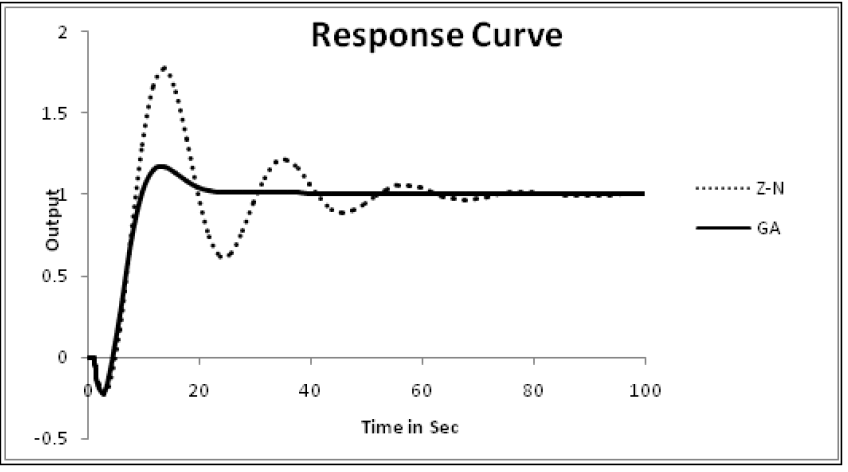 |
| The traditional and the intelligent techniques were compared and the output curve is plot with respect to time. |
C. Objective Functions & Error Values |
| This is the foremost difficult part of making a genetic algorithm program. The target perform is needed to judge the simplest PID controller for the system. An objective perform may well be created to seek out a PID controller that provides the littlest overshoot, quickest rise time or fastest sinking time. But so as to mix all of those objectives it absolutely was set to style an objective perform which will minimize the error of the controlled system instead. Everybody within the population is passed into the target perform one at a time. The body is then evaluated and assigned variety to represent its fitness, the larger its range the higher its fitness. The genetic algorithmic program uses the chromosomes fitness worth to make a replacement population consisting of the fittest members. |
| The integral error is usually accepted as an honest live for system performance. ItâÃâ¬ÃŸs helpful to possess criteria that place very little weight on the initial error. These integrals are finite as long as the steady- state error is zero. Not like easy criteria that use solely isolated characteristics of dynamic response, the standards of the class are supported the complete response. The followings are some unremarkably used criteria supported the integral error for a step point or disturbance response: |
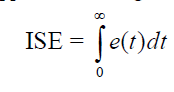 |
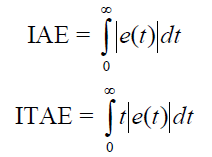 |
 |
D. Time Domain Specifications |
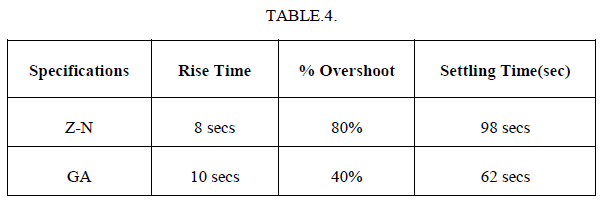
| From the response curve the time domain specifications like rise time, % over shoot and settling time values were obtained and it is tabulated in table 4. |
 |
CONCLUSION |
| This paper proposes a traditional tuning techniques and intelligent tuning approach for nonlinear conical tank process. By comparing the results the genetic algorithm based tuning provides the better results for the nonlinear process. From the simulation results, the response of the Genetic Algorithm was proved satisfactory in terms of rise time, percentage overshoot & settling time when compared with conventional techniques. The Error values are also reduced using Genetic Algorithm. From the system response, it is observed that the Genetic Algorithm tracks the set point with smooth transition and with less oscillation compared with Z-N method. From the simulation results, it is observed that the performance of Genetic Algorithm is better for the nonlinear conical tank process. |
References |
|