ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Nadeena M1, S.Sangeetha, M.E, 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
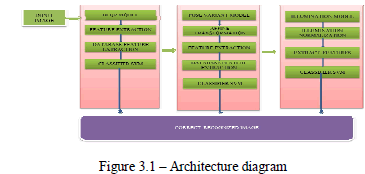
Although face recognition has been actively studied over the past decade, still recognizing faces appearing in unconstrained, natural conditions remains a challenging task. Recently, researchers have begun to investigate face recognition under unconstrained conditions that is referred to as unconstrained face recognition The state-of-the-art recognition systems yield satisfactory performance only under controlled scenarios like photographs taken under controlled light, background etc. Recognition accuracy degrades significantly when confronted with unconstrained situations. The main factors that make this problem challenging are image degradation due to blur and appearance variations due to illumination and pose. In this project the problem of blur, pose and illumination are jointly addressed. Here a Robust recognition of Blurred faces is proposed which assumes a symmetric constraint for the blur depending on several types of blur and visual features can be optimally integrated. Then faces under different pose have been recognized by normalizing it using affine transformation. Here an input face image is normalized to frontal view using the irises information. Use affine transformation parameters to align the input pose image to frontal view. After completing the aforementioned pose normalization process, the resulting final image undergoes illumination normalization. This is performed using the SQI algorithm. Finally Support vector machine classifier is adapted to uniquely identifying facial characteristics by classifying the face feature in training and testing set.
Index Terms |
| SQI algorithm, robust recognition of blurred faces, unconstrained face recognition |
I. INTRODUCTION |
| The objective of face detection is to find and locate faces in an image. It has been actively studied over the past decade. Face recognition is one of the most relevant applications of image analysis. It’s a true challenge to build an automated system which equals human ability to recognize faces. Although humans are quite good identifying known faces, it requires great skill to deal with a large amount of unknown faces. The computers, with an almost limitless memory and computational speed, should overcome human’s limitations. Face recognition has gained substantial attention over in past decades due to its increasing demand in security applications like video surveillance and biometric surveillance. Modern facilities like hospitals, airports, banks and many more another organizations are being equipped with security systems including face recognition capability. Despite of current success, there is still an ongoing research in this field to make facial recognition system faster and accurate. An important scenario is robust face recognition. |
| Robust face recognition requires the ability to recognize identity despite many variations in appearance that the face can have in a scene. The state-of-the-art recognition systems yield satisfactory performance only under controlled scenarios i.e. photographs taken under controlled light, background etc. Recognition accuracy degrades significantly when confronted with unconstrained situations. Examples of unconstrained conditions include illumination, pose variations, and so on. Still, recognizing faces appearing in unconstrained, natural conditions remains a challenging task. The main factors that make this problem challenging are image degradation due to blur and appearance variations due to illumination and pose. In this project the main focus is on jointly handling both the problems of image degradation. Support vector machine classification is incorporated for scaling to large real life databases and pose variation has also been modeled under this. |
II. RELATED WORK |
| An obvious approach to recognizing blurred faces would be to deblurr the image first and then recognize it using traditional face recognition techniques. However, this approach involves solving the challenging problem of blind image deconvolution [11]. A direct approach for face recognition has been proposed [15]. It can be shown that the set of all images obtained by blurring a given image forms a convex set, and more specifically, this set is the convex hull of shifted versions of the original image. Thus with each gallery image we can associate a corresponding convex set. Based on this set-theoretic characterization, we propose a blur-robust face recognition algorithm. In the basic version of the algorithm, the distance of a given probe image (which we want to recognize) from each of the convex sets is computed, and assign it the identity of the closest gallery image. The distance computation steps are formulated as convex optimization problems over the space of blur kernels. |
| Further, the algorithm can be made robust to outliers and small pixel misalignments by replacing the Euclidean distance by weighted L1-norm distance and comparing the images in the LBP (local binary pattern) space. It has been shown that all the images of a Lambertian convex object, under all possible illumination conditions, lie on a lowdimensional (approximately nine dimensional) linear subspace [2]. Though faces are not exactly convex or Lambertian, they can be closely approximated by one. Thus each face can be characterized by a low dimensional subspace, and this characterization has been used for designing illumination robust face recognition algorithms. Based on this illumination model, the set of all images of a face under all blur and illumination variations is a biconvex set. If the blur kernel is fixed then the set of images obtained by varying the illumination conditions forms a convex set; and if the is fixed illumination condition then the set of all blurred images is also convex. |
III. PROPOSED SYSTEM |
| In the proposed approach it can be seen that blur, pose variation and illumination are taken together. At first the blur portion alone is considered. It can be resolved with the help of direct recognition of blurred faces algorithm. Later on it is checked with the illumination correction algorithm. Basically a blurred image consists of sharp image and a blur kernel. The main issue here is to resolve the blur kernel or PSF i.e. point spread function. Many methods have been proposed like blind image deconvolution etc. but none proved that futile. Each and every method has got some drawback or the other. Blind image deconvolution finds the unknown blur kernel in a probabilistic manner and retrieves the image. Though this method returns correct results it is much time consuming. Also it does not consider any characteristics for the particular blur. In the latest cases like in the direct recognition approach it considers the characteristics of the blur. The blurs has got a number of characteristics like out of focus blur has circular symmetry etc. |
| All these features can be incorporated for getting the bur kernel sooner. In our aaproach of direct recognition of the blur it has got a database set preferably a ferret database. In the database each and every possible image is stored. It can be done in the following way. Then faces under different pose has been recognized by normalizing it using affine transformation. Here An input face image is normalized to frontal view using the irises information. Use Affine transformation parameters to align the input pose image to frontal view. After completing the aforementioned pose normalization process, the resulting final image undergoes illumination normalization. This is performed using the SQI algorithm. Finally Support vector machine classifier is adopted to uniquely identifying facial characteristics by classifying the face feature in training and testing set. |
| 3.1 Implementing Direct Recognition of Blurred Images |
| In this step we first review the convolution model for blur. Convolution operation performs the artificial blurring of images in the database.Next, we show that the set of all images obtained by blurring a given image is convex and finally we present our algorithm for recognizing blurred faces. Blurred image can be called as a combination of the sharp image and a blur kernel. So once the blur kernel is estimated it becomes easy for recognition. As a first stage the blur kernel is estimated giving the sufficient constraints to make it perform better. |
| Algorithm DRBF/rDRBF |
| In put : (Blurred) probe image Ib and a set of gallery images Ij. |
| Output: Identity of the probe image |
| Steps: |
| 1. For each gallery image Ij, find the optimal blur kernel. |
| 2. Blur each gallery image Ij with its corresponding hj and extract LBP features. |
| 3. Compare the LBP features of the probe image Ib with those of the gallery images and find the closest match. |
| 3.2 Recognition of blurred faces |
| Face recognition is also sensitive to small pixel misalignments and, hence, the general consensus in face recognition literature is to extract alignment insensitive features, such as Linear Binary Patterns (LBP), and then perform recognition based on these features. We then blur each of the gallery images with the corresponding optimal blur kernels hj and extract LBP features from the blurred gallery images. And finally, we compare the LBP features of the probe image with those of the gallery images to find the closest match. To make our algorithm robust to outliers, who could arise due to variations in expression, we propose to replace the L2 norm by the L1 norm. |
| 3.3 Incorporating the Illumination and pose normalization |
| Pose normalization increases classification accuracy. It simultaneously corrects both pose and illumination changes. When the number of faces to be recognized is sufficiently high the computational cost is incomparable. The head rolling case of pose normalization is corrected by means of centre of eyes [Fig. 4(a)]. The distances dl and dr interprets the distance between the external corners of eye position left and right respectively along with the tip position of the nose [Fig. 4(b)].Mainly this helps to identify the better exposed half of the face. If (dr>dl),that is if right half is the better exposed part then the corresponding image is left unchanged, otherwise perform a horizontal flip it means to reflect with respect to vertical axis. Therefore right region of the face is being taken for processing the images. The boundary region of the left region and right region of the face is marked by the points in Fig. 4(c) .The points making up the central line that ideally divides the face and the face ROI borders delimit the right and left face regions. The set of points that is placed centrally divides the right and left regions of the face and the ROI borders limit the right and left face regions. |
 |
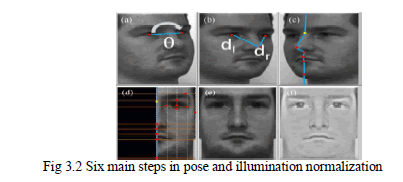 |
| The right half of the face is considered as the best exposed region of the face. All the rows are made of equal length by means of a stretching operation. The image to be processed is divided into horizontal and vertical bands by the lines passing through the points as shown in Fig. 4(d). The points have to be chosen in such a way that it allows to delimit the regions of the face. The choice of the points to use is such that it allows the delimitation of bands that are most significant to drive the normalization process, namely, those containing the eyebrow, the eye, the nose, and the mouth. The necessary resizing operations are done so that the interest points that are chosen by us fall in the predetermined positions. The left half face is reconstructed by reflecting the right half one [Fig. 4(e)]. This step is often performed to allow the normalization procedure even when the corresponding matching routine exploits the measures related to the whole face that is the distance between the eyes. The left half of the face is not reconstructed to merely exploit measures like interocular distance. |
| The recognition of the face is completely done so that all the methods is applicable with the facial components recognized. The experimental results portraits its overall effectiveness. After completing the above mentioned pose normalization process, the resulting final image undergoes illumination normalization. This is performed using the efficient SQI algorithm. The Self- Quotient image Q of image I is the smoothed version of I, F is the smoothing kernel, and the division is point-wise as in the original quotient image. Q is the Self- Quotient Image because it is derived from one image and has the same quotient form as that in the quotient image method |
ALGORITHM – ILLUMINATION NORMALIZATION USING SQI ALGORITHM |
| Input |
| ïÃâ÷ Pose normalized image |
| Steps |
| 1. Select several smoothing kernel G1, G2, …, Gn and calculate corresponding weights W1, W2, …, Wn according to image I, and then smooth I by each weighed filter Wgi. |
| 2. Calculate self-quotient image between each input image I and its smoothing version |
| 3. Transfer self-quotient image with nonlinear function |
| 4. Summarize nonlinear transferred results |
| Output |
| ïÃâ÷ Find closest match image |
| The image pixels value is continually divided by the mean of the values in its neighborhood, it is represented by a square mask of size k The overall normalization process is shown in Fig 4(f). |
| 3.4 Face Recognition across Blur, pose and illumination using SVM |
| The Face recognition is difficult because of the changeable illumination conditions and the image degradation problem of blur. The illumination changes between indoor and outdoor environments and it remains an unsolved problem for face recognition. Another main factor is that it is a multi-class problem. It can be solved by two familiar class margin approaches. The assumption is that N is the number of classes representing N different individuals. The first concept is ″one against the rest approach″. In this technique it includes N binary classifiers, and each of them performs the separation of a single class from all the remaining classes. The final output is the class that corresponds the highest output value for that binary classifier. The second proposal is ″one against one approach″. In this technique it includes N (N-1)/2 binary classifiers, and each of them separates a pair of given classes. The decision tree or voting is used for deciding the final output. |
| The first proposal is most efficient for our system. Two issues should be addressed in face recognition.(1) Determine the features to be used to represent a face. (2) Determine the utilization of these features for recognition. |
| This section presents an efficient classifier such as support vector machine for face recognition.SVM is an efficient and promising classification and regression technique. The main idea of SVM is like perform (1) a nonlinear mapping of the input space to a high dimensional feature space, and (2) given two linearly separable classes, the classifier has to be decided that leaves the maximum margin from two classes in the feature space. Because of the good performance of SVM it has been applied extensively for pattern classification and handwriting recognition. |
| Let the training set be X and the feature vectors are represented by x i, i = 1, 2 . . . , N. There mainly are two classes ω1, ω, and all the acquired feature vectors are either belonging to these two classes which are assumed to be linearly separable. The main aim is design the decision hyper plane. The decision hyper plane is also called Optimal Separating Hyper plane (OSH).Such a decision plane avoids the risk of misclassifying the training set and the testing set. For a two class classification problem, the decision hyper plane separates the two classes by the available samples. |
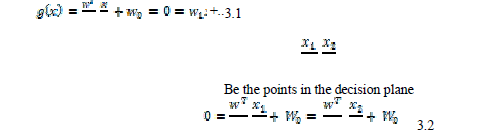 |
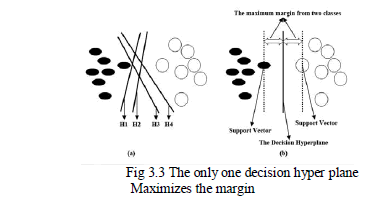
| Consider the samples in Fig. 5(a), here there are various possible linear classifiers given as H1, H2, H3 and H4 that can separate the data. Even tough there are many linear classifiers but there is only one decision hyper plane (shown in Fig. 5(b)) that maximizes the margin that is the in between distance between the data points of classes and the decision hyper plane. In reasonable amount of time SVM’s statistical learning theory is used to solve these problems. |
 |
IV. EXPERIMENTAL RESULTS |
| In the existing method it can be seen that different blur removal techniques were used. But the time consumed was much more and does not return accurate results. But in the proposed approach it can be seen that it much faster and returns more accurate results when compared with the previous approaches. It can be pictorially shown as follows. |
 |
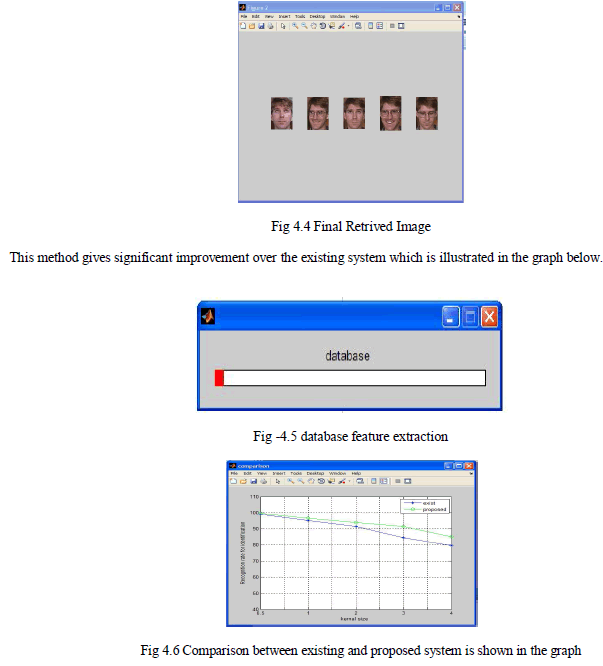 |
V. CONCLUSION |
| In our research, robust face recognition algorithm for recognizing faces from a distant image is proposed. Recognition accuracy degrades significantly when confronted with unconstrained situations. In this project the problem of unconstrained face recognition is addressed on blurred, pose variant and poorly illuminated faces. It has been shown that the set of all images obtained by blurring a given image is a convex set given by the convex hull of shifted versions of the image. Based on this set-theoretic characterization, a blur-robust face recognition algorithm is proposed. In this algorithm easily incorporate prior knowledge on the type of blur as constraints. Using affine transformations the face is pose normalized and illumination normalization is done using SQI algorithm. For scaling to large datasets a better classification method called support vector machine is incorporated into this for the training and testing set. |
References |
|