Unsupervised Distance-Based Outlier
Detection Using Nearest Neighbours
Algorithm on Distributed Approach: Survey

Jayshree S.Gosavi; Vinod S.Wadne

Unsupervised Distance-Based Outlier Detection Using Nearest Neighbours Algorithm on Distributed Approach: Survey

Jayshree S.Gosavi¹, Vinod S.Wadne²

PG Student, Department of Computer Engineering, ICOER, Savitribai Phule Pune University, Wagholi, Pune, India
Assistant Professor, Department of Computer Engineering, ICOER, Savitribai Phule Pune University, Wagholi, Pune, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Outlier detection is the process of finding outlying pattern from a given dataset. Outlier detection became important subject in different knowledge domains. Data size is getting doubled every years there is a need to detect outliers in large datasets as early as possible. In high-dimensional data outlier detection presents various challenges because of curse of dimensionality. By examining again the notion of reverse nearest neighbors in the unsupervised outlier-detection context, high dimensionality can have a different impact. In high dimensions it was observed that the distribution of points in reverse-neighbor counts becomes skewed .This proposed work aims at developing and comparing some of the unsupervised outlier detection methods and propose a way to improve them. This proposed work goes in details about the development and analysis of outlier detection algorithms such as Local Outlier Factor(LOF), Local Distance-Based Outlier Factor(LDOF) , Influenced Outliers and .The concepts of these methods are then combined to implement a new method with distributed approach which improves the results of the previous mentioned ones with reference to speed, complexity and accuracy.

Keywords

Outlier detection, high-dimensional data, reverse nearest neighbors, unsupervised outlier detection methods.

INTRODUCTION

Detection of outliers in data defined as finding patterns in data that do not conform to normal behavior or data that do not conformed to expected behavior, such a data are called as outliers, anomalies, exceptions. Anomaly and Outlier have similar meaning. The analysts have strong interest in outliers because they may represent critical and actionable information in various domains, such as intrusion detection, fraud detection, and medical and health diagnosis. An Outlier is an observation in data instances which is different from the others in dataset. There are many reasons due to outliers arise like poor data quality, malfunctioning of equipment, ex credit card fraud.

Data Labels associated with data instances shows whether that instance belongs to normal data or anomalous. Based on the availability of labels for data instance, the anomaly detection techniques operate in one of the three modes are 1) Supervised Anomaly Detection, techniques trained in supervised mode consider that the availability of labeled instances for normal as well as anomaly classes in a a training dataset. 2) Semi-supervised Anomaly Detection, techniques trained in supervised mode consider that the availability of labeled instances for normal, do not require labels for the anomaly class. 3) Unsupervised Anomaly Detection, techniques that operate in unsupervised mode do not require training data.

There are various methods for outlier detection based on nearest neighbors, which consider that outliers appear far from their nearest neighbors. Such methods base on a distance or similarity measure to search the neighbors, with Euclidean distance. Many neighbor-based methods include defining the outlier score of a point as the distance to its kthnearest neighbor (k-NN method), some methods that determine the score of a point according to its relative density, since the distance to the kth nearest neighbor for a given data point can be viewed as an estimate of the inverse density around it.

II. RELATED WORK

Author [2] assign an anomaly score known as Local Outlier Factor (LOF) to a given data instance. For any given data instance, the LOF score is equal to ratio of average local density of the k nearest neighbors of the instance and the local density of the data instance itself. To find the local density for a data instance, the authors first find the radius of the smallest hyper-sphere centered at the data instance that contains its k nearest neighbors. The local density is then computed by dividing k by the volume of this hyper-sphere. For a normal instance in a dense region, there local density will be similar to that of its neighbors, if its local density will be lower than that of its nearest neighbors , then it is an anomalous instance,. Hence the anomalous instance will get a higher LOF score. In [3] Author propose outlier detection approach, named Local Distance-based Outlier Factor (LDOF), which used to detect outliers in scattered datasets. In this to measure how much objects deviate from their scattered neighborhood. uses the relative distance from an object to its neighbors. The higher violation in degree of an object has, the mostly object is an outlier. In [4] proposed on a symmetric neighborhood relationship measure considers both neighbors and reverse neighbors of an object when estimating its density distribution .To avoid problem, when outliers are in the location where the density distributions in the neighborhood are significantly different.

In [5] Author propose a data stream outlier detection algorithm SODRNN based on reverse nearest neighbor. Deal with the sliding window model, to detect anomalies outlier queries are performed in order in the current window. Improves efficiency by update of insertion or deletion only in one scan of the current window.

In [6] propose a outlier ranking based on the objects deviation in a set of relevant subspace projections. It excludes irrelevant projections showing no clear difference between outliers and the residual objects and find objects deviating in multiple relevant subspaces, tackle the general challenges of detecting outliers hidden in subspaces of the data. In [7]Author propose a unification of outlier scores provided by various outlier models and a translation of the arbitrary “outlier factors” to values in the range [0,1] interpretable as values describing the probability of a data object of being an outlier. In [8] propose a new approach for parameter-free outlier detection algorithm to compute Ordered Distance Difference Outlier Factor. Formulate a new outlier score for each instance by considering the difference of ordered distances. Then, use this value to compute an outlier score.

III. EXISTING SYSTEMS

A. Local outlier factor (LOF:

In LOF, compare the local density of a instances with the densities of its neighborhood instances and then assign anomaly score to given data instance. For any data instance to be normal not as an outlier, LOF score equal to ratio of average local density of k nearest neighbor of instance and local density of data instance itself. To find local density for data instance, find radius of small hyper sphere centered at the data instance. The local density for instances is computed by dividing volume of k,i.e k nearest neighbor and volume of hyper sphere. In this assign a degree to each object to being an outlier known as local outlier factor. Depends on the degree it determines how the object is isolated with respect to surrounding neighborhood. The instances lying in dense region are normal instances, if their local density is similar to their neighbors, the instances are outlier if there local density lower than its nearest neighbor.LOF is more reliable with top-n manner. Hence it is called as top-n LOF means instances with highest LOF values consider as outliers.

B. Local distance based outlier factor(LDOF):

Local distance based outlier factor Measure the objects outlierness in scattered datasets . In this uses the relative location of an object to its neighbors to determine the object deviation degree from its neighborhood instances. In this scattered neighborhood is considered. Higher deviation in degree data instance has, more likely data instance as an outlier. In this algorithm calculates the local distance based outlier factor for each object and then sort and ranks the n objects having highest LDOF value. The first n objects with highest LDOF values are consider as an outlier.

C. Influenced Outlierness (INFLO):

This algorithm considers the circumstances when outliers are in the location where neighborhood density distributions are significantly different, for example, in the case of objects close to a denser cluster from a sparse cluster, this may give wrong result. This algorithm considers the symmetric neighborhood relationship. In this considering influence space and when estimating its density distribution also considers both neighbors and reverse neighbors of an object .Assign each object in a database a influenced outlierness degree. The higher inflo means that the object is an outlier.

D. Disadvantages:

1. Threshold value is used to differentiate outliers from normal object and lower outlierness threshold value will result in high false negative rate for outlier detection .

2. Problem arises when data instance is located between two clusters, the interdistance between the object of k nearest neighborhood increases when the denominator value increases leads to high false positive rate.

3. Needs to improve to compute outlier detection speed.

4. Needs to improve the efficiency of density based outlier detection.

IV. PROPOSED SYSTEM

A. Description of the Proposed system:

An input of collection of large data set will be provided to the proposed system, as data is collected from standard data set repositories, data preprocessing will be applied before passing data to the next phase of the system. Further, this preprocessed input is being passed through to the partition module, where these datasets are been partitioned among many nodes from that one of the node is supervisor node and generate partition statistics and this statistical data is been visualized. After this, in outlier detection module,distributed algorithms is proposed on the preprocessed input data set for identifying outliers. These results will be evaluated for proposed algorithmic distributed approaches in the performance evaluation.

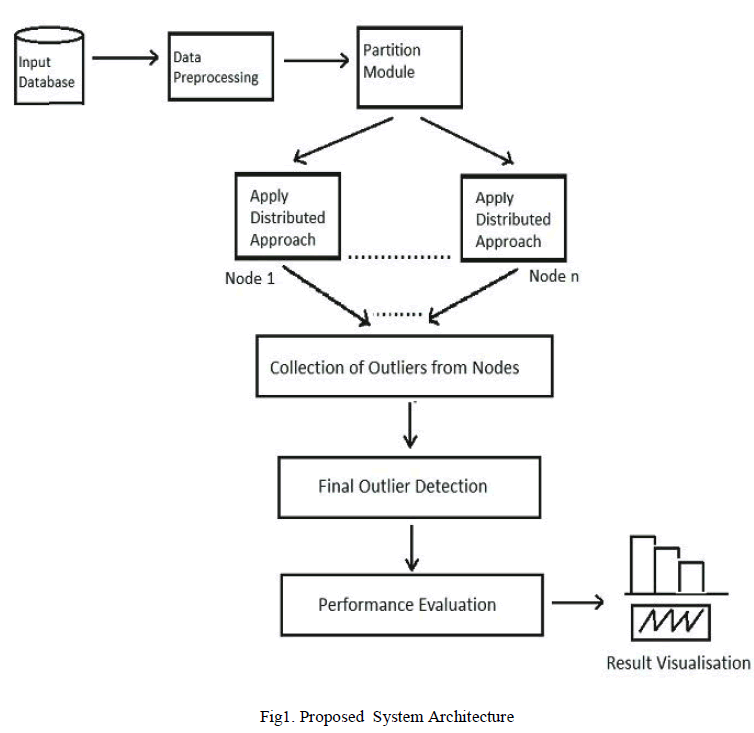1) Data collection and data preprocessing :

In data collection the initial input data for this system will be collected from standard dataset portal i.e. UCI data set repository. As proposed in system, the standard dataset will be used for this system includes Cover type, IPS datasets. Collected datasets may be available in their original, uncompressed form therefore; it is required to preprocess such data before forwarding for future steps. To preprocess large dataset contents, techniques available is data mining such as data integration, data transformation, data cleaning, etc. will be used and cleaned, required data will be generated.

2) Data partitioning:

In this module, as stated earlier in system execution plan, the preprocessed data is divided into number of clients from central supervisor node i.e. server as per the data request made by desired number of clients. This partitioned data will be then processed by individual clients to identify outliers based on applied algorithm strategy.

3) Outlier detection:

The technique proposed for identifying outliers will be applied initially at distributed clients and their results of detected outliers would be integrated on server machine at final stage computation of outliers. To do this, the outlier detection strategies proposed are KNN Algorithm with ABOD and INFLO Method.

The Distributed approach proposed with above Method based on anomaly detection techniques based on nearest neighbor .In this technique assumption is that normal data instances occur in dense neighborhoods, while outliers occur far from their nearest neighbors. In this proposed work using concepts of nearest neighbor based anomaly detection techniques:(1) use the distance of a data instance to its kth nearest neighbors to compute the outlier score.(2) compute the relative density of each data instance to compute its outlier score.

The proposed algorithm consider the k-occurrences defined as dataset with finite set of n points and for a given point x in a dataset, denote the number of k-occurrences based on given similarity or distance measure as Nk(x),that the number of times x occurs among all other points in k nearest neighbor and points those frequently occurred as a hubs and points those occur infrequently as a antihub.Uses reverse nearest neighbors for instance , finding the instances to which query object is nearest. In this first read the each attribute in high dimensional dataset, then using angle based outlier detection technique compute the distance for every attribute using dataset Set distance and compare with distance from each instance and assign the outlier score. Based on that outlier score using reverse nearest neighbor determine that particular instance is an outlier or not.

4) Performance Evaluation and Result Visualization :

In this module, the outlier detected by above approach will be evaluated on the basis of set evaluation parameters for their performance evaluation. The performance evaluation will also provide details about implemented system performance metrics, constraints and directions for future scope. With the help of proper visualization of results, the system execution will be made more understandable and explorative for its evaluators.

V. EXPERIMENTAL SETUP AND EVALUATION

Our tests were performed using high dimensional dataset that is Cover Type dataset from UCI machine learning Repository which contains 54 number of attribute and number of instances are 581012.The experimental evaluation was performed on an Intel two core CPU at 2.53 GHz and 4 GB of RAM, having a windows as its operating system. The algorithm was fully implemented in Java to process data instances in high dimensional data.

VI. CONCLUSION

This proposed KNN Algorithm with ABOD and INFLO Method with unsupervised learning using distributed approach aims at implement and comparing few of the unsupervised outlier detection methods and propose a way to improve them in terms of speed and accuracy, reducing the false positive error rate, reducing the false negative rate and improve the efficiency of density based outlier detection and comparison with the existing algorithms. The future implementation is in machine learning techniques such as supervised and semi-supervised methods.

References

V. Chandola, A. Banerjee, and V. Kumar, “Anomaly detection: A survey,” ACM Comput Surv, vol. 41, no. 3, p. 15, 2009.
M. M. Breunig, H.-P. Kriegel, R. T. Ng, and J. Sander, “LOF: Identifying density-based local outliers,” SIGMOD Rec, vol. 29, no. 2, pp. 93–104, 2000.
K. Zhang, M. Hutter, and H. Jin, “A new local distance-based outlier detection approach for scattered real-world data,” in Proc 13th Pacific-Asia Conf on Knowledge Discovery and Data Mining (PAKDD), pp. 813–822. 2009.
W. Jin, A. K. H. Tung, J. Han, and W. Wang, “Ranking outliers using symmetric neighborhood relationship,” in Proc 10th Pacific-Asia Conf on Advances in Knowledge Discovery and Data Mining (PAKDD), pp. 577–593, 2006.
C. Lijun, L. Xiyin, Z. Tiejun, Z. Zhongping, and L. Aiyong, “A data stream outlier delection algorithm based on reverse k nearest neighbors,” in Proc 3rd Int Symposium on Computational Intelligence and Design (ISCID), pp. 236–239, 2010.
Emmanuel Milller, Matthias Schiffer , Thomas Seidll,”Statistical Selection of Relevant Subspace Projections for Outlier Ranking”,IEEE, ICDE Conference,pp. 434 - 445 ,2011.
Hans-Peter Kriegel Peer Kr¨oger Erich Schubert Arthur Zimek,” Interpreting and Unifying Outlier Scores”,SIAM International Conference on Data Mining (SDM), Mesa, pp. 13–24. AZ, 2011.
Nattorn Buthong, Arthorn Luangsodsai, Krung Sinapiromsaran,” Outlier Detection Score Based on Ordered Distance Difference,” International Computer Science and Engineering Conference (ICSEC),pp. 157 – 162, 2013.
H.-P. Kriegel, M. Schubert, and A. Zimek, “Angle-based outlier detection in high-dimensional data,” in Proc 14th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining (KDD), pp. 444–452, 2008.