ISSN: 2320-0189
ISSN: 2320-0189
Nixon Tongun1,2* and Guixia Wang1
1Jilin Agricultural University, College of Economics and Management, Department of Agricultural Economics and Management, Changchun, P.R. China
2Department of Agricultural Sciences, College of Natural Resources and Environmental Studies, University of Juba, Juba, South Sudan
Received Date: 14/09/2018; Accepted Date: 26/09/2018; Published Date: 29/09/2018
Visit for more related articles at Research & Reviews: Journal of Botanical Sciences
Many development projects were implemented in South Sudan with the aim of increasing agricultural productivity. However, little empirical evidence exists of their impacts on the productivity. This paper aims at assessing the impact of Support to Agriculture and Forestry Development Project (SAFDP) on maize productivity of small-scale farmers in South Sudan using the propensity score matching method. 200 maize farmers, 80 participants and 120 non-participants were sampled. Results obtained from the model indicated that the impact of the project on maize productivity was statistically significant. Tentatively, participant farmers obtained higher maize yields than the non-participating farmers did. Therefore, policies geared at providing financial support to farmers will help a lot in increasing maize productivity in the study area.
Impact, SAFDP, Maize productivity, Propensity score matching, South sudan.
Maize is both a major food crop as well as a commercial crop in South Sudan. Most maize farmers are small-scale who practice subsistence farming. The potential for expanding maize production in South Sudan is huge. However, despite the enormous potential, South Sudan is failing to reach self-sufficiency in the sense of being able to meet its domestic annual food needs. Thus, the key challenge in South Sudan today is how to increase domestic food production so as to reduce over-dependence on imports and donations. Maize is the second most important cereal grain in South Sudan after sorghum. Maize and sorghum account for about 50 to 75 percent of total household production [1]. In the other regions, maize is normally cultivated in limited areas close to homesteads for green cob consumption as vegetables. Maize is consumed roasted/boiled or cooked in South Sudan. Maize is milled into maize flour used for making porridge, gruel or couscous and local bread called asida. It is also used as feed for livestock and poultry. Maize accounts for 22-25 percent of starchy staple consumption in Africa, representing the largest single source of calories followed by cassava [2]. Most maize farmers in South Sudan are small-scale who practice subsistence farming. Farmers use hand tools such as hoes, malodas, pangas, and sickles which greatly limit the area of land that can be cultivated by farm households. Farmers commonly use their own seed saved from the previous year’s harvest, and virtually no commercial fertilizers, pesticides or herbicides are used.
Following the one country two systems principle in the Comprehensive Peace Agreement (CPA) in 2005, four major government interventions were put in place in the area of Agriculture. Firstly the Sudan Productive Capacity Recovery Program whose aim was to contribute to reducing the levels of poverty and food insecurity, co-financed by the Government of Sudan and the European Commission. Second was the Sudan Institutional Capacity Program: Food Security Information for Action, which aimed at contributing to food security by supporting and strengthening policy and planning initiatives of food security and market information systems, funded by the European Union. The third was the South Sudan Livelihoods Development Project co-financed by Government of Southern Sudan, International Fund for Agricultural Development (IFAD) and the Embassy of the Kingdom of Netherlands, meant to support communities. Finally, was the support to Agriculture and Forestry Development Project. The former two projects were implemented in both Northern and Southern Sudan while the latter two projects were implemented only in South Sudan [3].
The government of South Sudan through the Ministry of Agriculture and Forestry launched the Support to Agriculture and Forestry Development Project in 2007 [4]. The project aimed at increasing productivity of some targeted 730 and 260 groups of agricultural and forestry producers respectively by facilitating adoption of improved technologies in agriculture and forestry; and by strengthening capacities of the central and state governments as well as the private sector to plan and deliver services in agriculture and forestry. The project aimed at addressing priority issues reflected within the Multi-Donor Trust Fund framework for sustained peace, development and poverty eradication. It is also consistent with the Ministry of Agriculture and Forestry’s strategic food and agriculture policy framework in which farming communities and natural resource-users participating directly in the development process of the support services are being empowered to become prime-actors in improving their own economic growth [4]. Farmer groups of 10 to 20 members were given 10,000 SSP and 16, 000 SSP in the first and second phases respectively, as grants [4].
Agricultural productivity is a key indicator for analysis of economic growth, which is a significant demand for policy makers. Increased productivity in agriculture has a number of advantages. Firstly, it increases the flow of resources from one sector to another, thereby enhancing economic growth. Secondly, a higher level of agricultural productivity results in lower food prices which increase consumers’ welfare. Thirdly, productivity growth improves the competitive position of a country’s agricultural sector. This paper therefore aims to assess the impact of Support to Agriculture and Forestry Development Project (SAFDP) on maize productivity, a crucial crop for food security and livelihoods in South Sudan.
Data Types and Collection Methods
The study was conducted in Juba and Morobo Counties of Central Equatoria State, Republic of South Sudan. These areas were chosen because of efforts by both government of South Sudan through its programs like SAFDP and NGOs to promote maize production in the state. The SAFDP participants were selected by a committee formed by the county agricultural department, who used a number of criteria such as farmer groups’ seasonal plans and their achievements in the previous years. The nonparticipants (control) were constructed by selecting a group of non-participants who resemble the participants in everything, but the fact of receiving the intervention using calliper and radius matching estimator technique. Using a multi-stage sampling technique, two payams in each county and two bomas in each payam were purposively selected. Ten (10) SAFDP and 15 non- SAFDP farmers per each boma were randomly selected, giving a sample size of 200; 80 project and 120 non-project farmers.
Analytical Methods
The Propensity Score Matching (PSM) Model
The PSM was used to analyze the impact of Support to Agriculture and Forestry Development Project on maize productivity. To achieve this objective, we use the PSM method as outlined below. Many studies that evaluate agricultural programs such as the impact of adopting improved technologies do not properly control for potential differences between the participants and nonparticipants, making it difficult to draw definitive conclusions [5-7]. Therefore, in the absence of non-random selection of farmers, simple comparisons of mean outcomes (such as yields) between participants and non-participants may yield biased estimates of the impact. To control for possible hidden selection bias, this study adapts the propensity score matching (PSM) method to overcome selection bias. We follow Rosenbaum & Rubin, Dehejia & Wahba, Jalan & Ravallion, Dehejia & Wahba, Smith & Todd, Mendola, Caliendo & Kopeinig [8-13]. PSM does not require exclusion restrictions or a given specification of the functional form of the selection model to construct the counterfactual as well as reduce self-selection bias.
Estimating the Average Treatment Effect
The counterfactual here is what would have happened to those farmers who, in fact, participated in the project, had they not participated. The key assumption is that individuals selected into participant and non-participant groups have potential outcomes in both states, the one in which they are observed and the one in which they are not observed [14]. We determine the average treatment effect on the treated (ATT) farmers, that is, the causal effect of SAFDP on maize yield. For a given participant we have the observed mean outcome under the condition of participating in the project as E (Y1 |D=1) and the unobserved (hypothetical) mean outcome that the participant would have realized had they not indeed participated in the project as E (Y0 |D=1). Similarly, for a given non-participant we have the observed mean outcome under the condition of non-participating in the project as E (Y0 |D=0) and the unobserved (hypothetical) mean outcome that the non-participant would have realized had they indeed participated in the project as E (Y1 |D=0). E is the expectation operator. Following the parameter of interest in this study is the ATT and is given as
ATT=E (Y1 - Y0 |D=1) =E (Y1 |D=1) – E (Y0 |D=1) (1)
Our central interest of impact evaluation is not in E (Y0 |D=0), but in E (Y0 |D=1). Therefore, PSM uses balancing scores to extract, for comparison, the observed mean outcome of those non-participants who are most similar in observed characteristics to the participants, that is, it uses E (Y0|D=0) to estimate the counterfactual, E (Y0 |D=1). In order for the true parameter to be estimated, we require that
E (Y0 |D=1) – E ( Y0 |D=0)= 0 (2)
This ensures that the ATT is free from self-selection bias.
Testing the Quality of Matching
Following Rosenbaum & Rubin formation of matched pairs of observationally similar participant and non-participant cases eliminates the confounding effects of observable variables. Matching is intended to restrict the control sample (non-participants) in order to increase the similarity of the sub-sample of control cases that are directly compared with the treated cases in order to estimate the impact of the SAFDP. Therefore the quality of covariate balancing (equality of means on the p-scores and equality of means on all covariates) between participants and non-participants is tested using the standardized bias (SB) between participant and non-participant samples as suggested by Rosenbaum & Rubin [15,16]. For each variable and propensity score, the standardized bias is computed before and after matching by the equation:
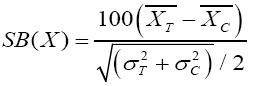 (3)
(3)
where 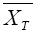 and
and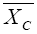 are the sample means for the treatment and control groups, and
are the sample means for the treatment and control groups, and
σ2T and σ2C are the corresponding variances.
The reduction in bias post matching (BR) can be computed as:
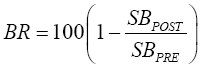 (4)
(4)
The BR ratio shows the percentage reduction in standardized bias due to matching. That is, the standardized bias measures the difference between covariate means of the treatment and control groups in terms of the number of standard deviations from zero [17]. Other covariate balancing indicators used are the likelihood ratio test of the joint significance of all covariates and the pseudo-R2 from a probit or logit of treatment status on covariates before matching and after matching on matched sample. After matching, there should be no systematic differences in the distribution of covariates between both groups. This implies that the pseudo-R2 should be fairly low and the joint significance of all covariates should be rejected.
Testing the Robustness of the Estimations
PSM estimators are not consistent estimators for treatment effects if the assignment to treatment is non-random, that is, if there are unobserved covariates that affect the assignment to treatment and are also related to the outcomes [18]. An unobserved covariate that affect assignment to treatment but that does not affect the outcome beyond the covariates already controlled for, does not challenge the robustness of the estimations. In order to estimate the extent to which such ‘selection on unobservables’ may bias the inferences, this study employs the Rosenbaum bounds sensitivity analysis which determines how strongly an unmeasured variable must influence the selection process so that it could undermine the implications of our matching analysis (ibid). If there is a certain unobserved variable of concern that affects the selection process then the probability of treatment is given by,
P(X) = Pr(D=1|X, u) = F(βX + γu) (5)
where X is a vector of all observed covariates and u represents the unobserved variable affecting assignment to treatment;
γ is the effect of u on the treatment probability.
If the estimator is free of hidden bias, γ is equal to zero and X solely determines the participation probability. However, if there is hidden bias, two individuals with the same observed covariates, X, have different chances of participating in the SAFDP. Consider a matched pair of individuals i and j, and logistic distribution F. The odds that an individual receives a treatment is given by, P/(1 − P). This means that for a matched pair of individuals i and j, the odds ratio is,
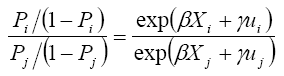 (6)
(6)
Since Xi=Xj, the odds ratio reduces to exp [γ(ui −uj )]. The bounds on the odds ratio that either of the two individuals receives the treatment is thus given by
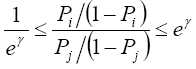 (7)
(7)
We denote eγ as Γ as is the standard case. If Γ=1, there will be no hidden bias as either γ=1 or ui = uj. That is, if Γ=1, individuals with the same observable characteristics have the same probabilities and odds of assignment to treatment. If Γ=2, then one individual with the same observable characteristics as another is twice as likely to be selected into the treated group. The bounds on the odds ratio start to vary as Γ takes on values greater than one, that is, we allow for the presence of unobserved variables to influence the assignment into treatment. The Rosenbaum bounds calculate at each value of Γ the point at which hidden bias causes us to question the findings. This cut-off point should be large enough to render our estimates robust against the presence of unobservable selection bias. By comparing the Rosenbaum bounds on treatment effects at different levels of Γ, we can assess the strength such unmeasured covariates must have in order that the estimated treatment effects from propensity score matching would have arisen purely through non-random assignment [18].
Impact of SAFDP on Maize Productivity: Covariate Balancing
The results from testing the quality of PSM matching (covariate balancing) are shown in Table 1 below. Matching, as expected, leads to a significant reduction in the standardized bias, the pseudo-R2, the likelihood ratio chi-square, and a reduction in the statistical significance of the likelihood ratio Chi-square. The Epanechnikov kernel matching algorithm results are shown in Table 1 below. The mean standardized bias (SB) reduction after matching for the maize yield of 2011 season two as an outcome variable is 35.38%. This shows a good level of covariate balancing. There is no formal criterion in the literature on the magnitude of the standardized bias reduction. Rosenbaum & Rubin (1985) suggest that a value of 20% is large enough. The pseudo-R2 statistic for the maize yield drops from 0.468 to 0.013 after matching for the 2011 season two maize yields as expected. Thus, the covariates have low explanatory power after matching for selection into the treatment group.
| Outcome Variable | Bias reduction | Pseudo R2 | Likelihood ratio Chi-square | p-value of Likelihood ratio |
|---|---|---|---|---|
| Maize Yield | 35.38% | 0.468 0.013 |
117.88 3.34 |
0.000 0.986 |
| Note: Numbers in bold italics are the before-matching statistics and numbers in regular font are the after-matching statistics. | ||||
Table 1: Covariate balancing test results for the PSM.
Finally, the p-values of the likelihood ratio Chi-square suggest that there are no systematic differences in the distribution of covariates between treatment and control cases after matching. The p-value after matching is 0.986. Thus, the hypothesis that both groups have the same distribution in the covariates after matching cannot be rejected and these results are used in the evaluation of the impact of SAFDP on the level of maize yields obtained by smallholder farmers.
ATT Estimation
Impact of SAFDP on Maize Yields
The average treatment effect on the treated (ATT) gives the difference between the observed mean maize yield obtained by the participants of SAFDP and the mean maize yield obtained by the non-participants. This difference is obtained after matching the two cohorts using PSM. The results are reported in Table 2 below and they show that participating in the SAFDP has a positive and significant effect on maize yields for maize farmers. Farmers who participated in the SAFDP consistently obtained higher maize yields than those who did not. Therefore, on average, the increment in the maize yield obtained in 2011 season two (relative to the mean maize yield of the control group) due to participating in the SAFDP is 82 kg/feddan. This difference is positive and statistically significant at 1% level of confidence.
| Outcome Variable | ATT | t-value | Γ (critical level of hidden bias) | Matched Pairs |
|---|---|---|---|---|
| Maize Yields (Season Two 2011) |
82 | 2.85*** | 2.3 2.6 |
71 |
| ***, ** and * indicate significance at 1%, 5%, and 10%, respectively. The figure in bold italics is the value of Γ at 5%. The value of Γ in regular font is at 10% level of confidence. | ||||
Table 2: Impact of SAFDP on maize yield in South Sudan.
Robustness Tests (Rosenbaum Bounds)
Sensitivity analysis using Rosenbaum bounds indicates that the results of the effect of SAFDP on maize yield obtained by smallholder farmers of maize were strongly robust to hidden selection bias. The critical value of Γ for the maize yield as an outcome variable was 2.3 at 5% level of confidence. This shows that the SAFDP has a positive and significant effect on maize yield obtained by farmers and the effect is strongly insensitive to hidden selection bias due to confounding factors.
We consider 10% level of confidence and following DiPrete and Gangl, we restrict ourselves to only the case of bounds for positive self-selection. Accordingly, the critical value of Γ=2.6 for the maize enterprise meaning that all maize farmers with the same observed X-vector of observable characteristics can differ in their odds of assignment to treatment by a factor of 2.6 before the confidence band around our ATT estimate starts to include zero. A critical value of Γ of 2.6 does not imply that there is unobserved heterogeneity or that the SAFDP has no effect on maize yields. It just simply means that a confounding variable would need to have an odds ratio change by a factor of 2.6 to completely overturn our ATT result. In other words, Γ=2.6 at 10% level of significance implies that doubts over the statistical significance of the estimated ATT becoming insignificant would emerge only if the confounding factor causes the odds ratio of assignment to the participant cohort to differ between the two cohorts (participant and non-participant) by a factor of 2.6 as indicated by DiPrete and Gangl. This means that even if we allowed the odds ratio of assignment to treatment to differ between participants and non-participants by a factor of about 2.6, the effect would still not be sensitive to hidden selection bias due to an unobserved or confounding variable. Therefore, on overall the results are strongly robust to hidden selection bias. We can confidently assert that the SAFDP has had a positive and significant impact on maize yields obtained by smallholder farmers. That is, the ATT estimates in this study are due to the effect of the SAFDP.
The SAFDP has had a positive and significant impact on maize yields obtained by smallholder farmers. Participation in the SAFDP confers certain benefits to maize farmers such as access to effective extension services and financial support necessary to purchase agricultural inputs such as improved seed. That is why their yields are higher than the non-participants. Therefore, there is need to strengthen the cohesion of farmers’ groups and increase awareness of farmers on the benefits of joining farmers’ groups for them to benefit from similar interventions as the SAFDP. One important contribution of the SAFDP was the development of human capital which could extend beyond the project lifecycle, where community extension workers were trained. Using this evidence, it can therefore be recommended that development projects like the SAFDP by the private or public sectors should be encouraged to stimulate and increase agricultural productivity in general and maize productivity in particular, in South Sudan.
This study is made possible by the scholarship fund awarded by Chinese Government through China Scholarship Council.