International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Vertex Magic Total Labeling of Complete Graphs and their application for Public-Key Cryptosystem

Krishnappa H K1, N K Srinath2 and S Manjunath3
  1. Assistant Professor, Dept. of CSE, RVCE, Bangalore, India
  2. Professor, Dept. of CSE, RVCE, Bangalore, India
  3. Professor, Dept. of Mathematics, BNMIT, Bangalore, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Achieving higher level of security in message transfer over networked environment and the efficiency of a cryptographic algorithm is based on its time taken for encryption / decryption and the way it produces different cipher text from a clear text. The RSA, the widely used public key algorithm and other public key algorithms may not guarantee that the cipher text is fully secured. As an alternative approach to handling ASCII characters in the cryptosystems, a vertex magic total labeling of complete graph is thought of in this work. It attempts to enhance the efficiency by providing add-on security to the cryptosystem. This approach will increase the security due to its complexity in encryption because it deals with the VMTL formation that cannot be easily traced. Here, encryption / decryption is based on numerals contained in VMTL table rather than ASCII values. This proposed work provides another layer of security to any public key algorithms such as RSA, ElGamal etc. Since, this model is acting as a wrapper to a public key algorithm; it ensures that the security is enhanced. Further, this approach is experimented in a simulated environment with 2, and 4 processor.

Keywords
VMTL, Public Key Cryptosystem, RSA, AES, Security.

INTRODUCTION
Graph labeling is an assignment of integers to the vertices or edges, or both, subject to certain conditions. Graph labeling was first introduced in the late 1960s. In the intervening years dozens of graph labeling techniques have been studied in over 1000 papers. Formally, for a given a graph G, a vertex labeling is a function mapping vertices of G to a set of labels. A graph with such a function defined is called a vertex-labeled graph. Likewise, an edge labeling is a function mapping edges of G to a set of labels. In this case, G is called an edge-labeled graph. When the edge labels are members of an ordered set (e.g. the real numbers), it may be called a weighted graph. Graph coloring is a special case of graph labeling, such that adjacent vertices and coincident edges must have different labels. The most complete recent survey of graph labeling is [1].
In [6] Gopinanath Ganapathy, and K. Mani showed how to achieve high level of security by using magic squares of order 16. Krishnappa H.K., N.K.Srinath and Ramakanth Kumar P. [5] showed that how to use magic squares to realize VMTL of complete graph Kn. After proving that labeling is available for different graphs, we shall go on to display a practical application of graph labeling in the field of cryptography.
The shared data must only be visible to a subset of users known as the authorized users. We shall attempt to make the secret shares verifiable using the concept of colored graphs (vertex magic labeled graphs).The integral idea is that every colored graph can be converted into a unique number and vice versa. This number allows for verification of shared secret. The number is not directly shared but is shared in the form of the colored graph. There are many ways to generate this unique number from a colored graph.
The efficiency of a cryptographic algorithm is based on the time taken for encryption/decryption and the way it produces different cipher text from a clear text. The RSA, the widely used public key algorithm does not guarantee full security.RSA mainly deals with encrypting individual characters based on its ASCII value. The VMTL (Vertex Magic Total Labeling) table approach acts as an add-on to the existing RSA algorithm. It acts like a wrapper. The objective of using VMTL is to increase the complexity in a non-linear fashion. The encryption in our algorithm will be complex because it deals with the VMTL graph/table formation with seed number, start number and a sum that cannot be easily traced. The encryption/decryption here is based on numbers got from the generated VMTL tables rather than directly encrypting the ASCII values.
Different mathematicians discussed the usefulness of magic labeling in practical applications. For example, in the field of Computer Science, magic labeling can be used to study the behavior of a network or identify erroneous behavior in a network. The purpose of this project is to assign values to vertices and edges of a complete graph so as to obtain the vertex magic total labeling of the same.
The security of many cryptographic systems depends upon the generation of unpredictable components such as the key stream in one –time pad, the secret key in the DES algorithms, the prime p and q in the RSA encryption etc. In all these cases, the quantities generated must be sufficient in size and random in the sense that the probability of any particular value being selected must be sufficiently small. However ,RSA is not semantically secure or secure against chosen cipher text attacks even if all parameters are chosen in such a way that it is infeasible to compute the secret key d from the public key(n,e),choosing p,q are very large etc. Even if the above said parameters are taken carefully, none of the computational problems are fully secured enough because to encrypt the plaintext characters, their ASCII values must be used and if a character occurs in several places in a plaintext there is a possibility of the same cipher text is produced. To overcome this problem, we are trying to develop a method to add further complexity to public key encryption with magic squares. Each VMTL table is considered as one ASCII table. Thus, instead of taking ASCII values for the characters to encrypt, preferably different numerals representing the position of ASCII values are taken from VMTL table and encryption is performed using these tables. We shall try magic constants of different orders.
The subject „Graph Theory and Combinatorics has been one of the subjects which gave an interdisciplinary perspective on the field of Computer Science and Engineering. The subject is immensely interesting primarily because of the application of mathematical logic to solve real world problems using the knowledge of Computer Sciences. Hence this topic was chosen to further pursue the same interest.
Our intention of attempting to solve the given problem is due to the increasing ease with which man in the middle attacks is being carried out with respect to public cryptography. With the increasing popularity of public key systems, hackers are basing their attacks based on previously existing available data. Thus, we attempt to increase the randomness of choosing cipher text while also sharing the public key via labeled graphs. Hence, first the VMTL is being used to encrypt the message, upon which the AES encryption is being performed. The symmetric key of the AES needs to be shared which are being done by using the RSA Public Key Crypto system.

REPRESENTATION
In this paper, the vertex magic total labeling for a complete graph Kn is represented as an (n x n) matrix, in which all the entries of the principle diagonal are used to label the vertices of the graph. The remaining entries of the matrix are used to label the edges. The final matrix, each column sum shall be a constant, called the magic constant. The construction of the labeling for Kn, is shown in [4].
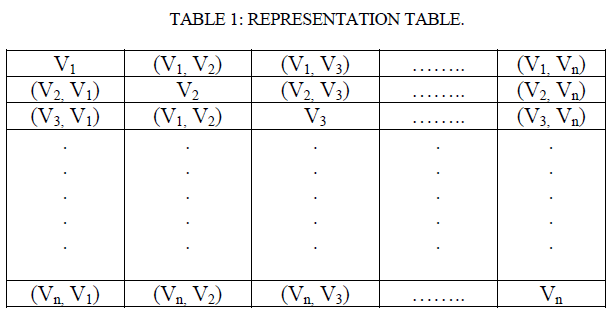image

DESIGN

A. VMTL OF Kn.
We use a K23 graph for total labeling. This is because we use the unique values generated by the labeling of the vertices and edges in order to assign blocks of data to these corresponding labels. The seed number as well as the position is taken from the user to generate the VMTL that corresponds to that detail. We use this particular size as the number of labels i.e. n + nC2 for the number 23 comes up to 276 which is the lowest number of labels above 256 – the number used for the ASCII set.
There are several ways to obtain VMTL of Kn for n odd [3, 4, 5]. We use the algorithm described by Krishnappa H.K., N.K.Srinath and others in [5] to generate the VMTL.
We use the bellow matrix to map the characters that are read sequentially from the text file to map it to the integer value that is stored in the table. For each particular character the ASCII equivalent is mapped to the table using looping constructs that sequentially search for the position in the matrices in order to map it. The decryption process uses the key i.e. the seed to regenerate the same matrix. It uses a simple lookup table in order to see what the positional values are. Using the positional values it creates the value of the number in the ASCII table in order to decrypt the file.
Encryption and decryption process involves generation of seed for RSA, AES and as well as the public and the private keys. To generate the matrices, a five digit magic sum as well as initial seed is provided as input. In addition to the magic sum, an initial starting value is also provided as input along with the file to be encrypted. The generated matrices are stored separately in a file. Decryption process is similar to the encryption process whose input is the intermediate file which is encrypted in the encryption process.
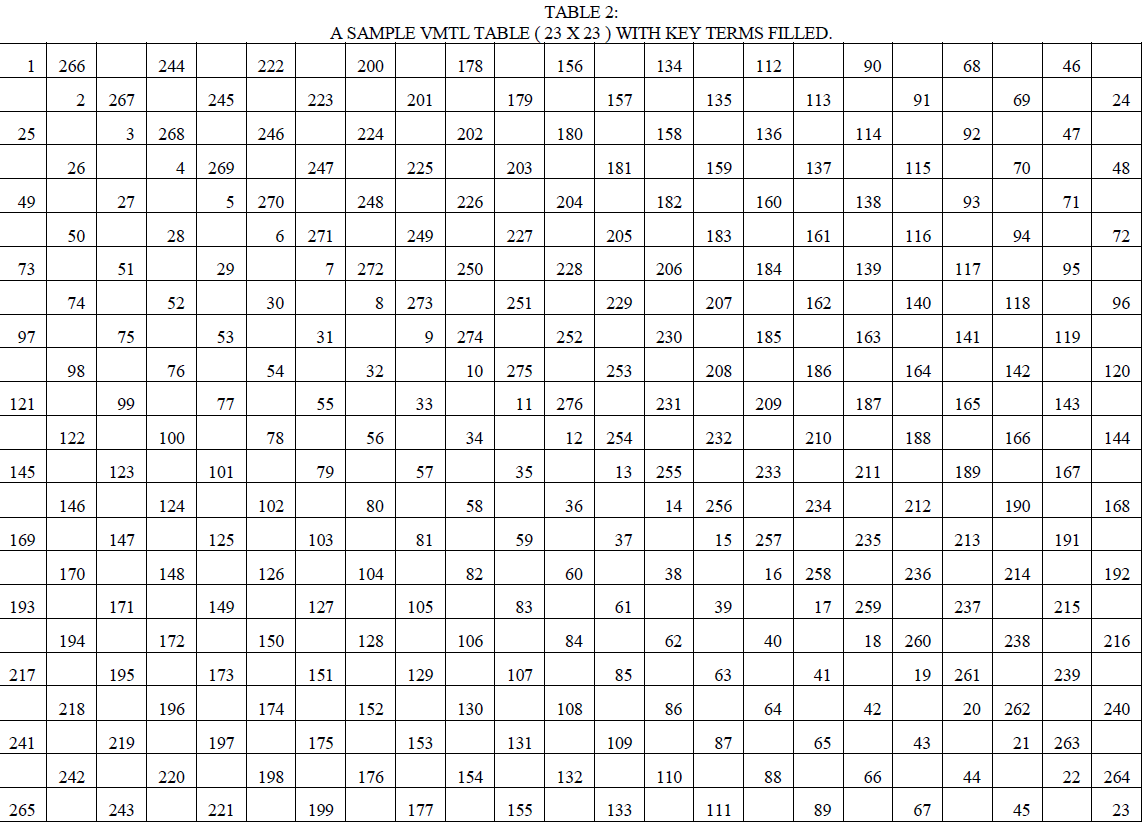image

B. ENCRYPTION/DECRYPTION PROCESS.
We use the above matrix to map the characters that are read sequentially from the text file to map it to the integer value that is stored in the table. For each particular character the ascii equivalent is mapped to the table using looping constructs that sequentially search for the position in the matrices in order to map it. The decryption process uses the key i.e. the seed to regenerate the same matrix. It uses a simple lookup table in order to see what the positional values are. Using the positional values it creates the value of the number in the ASCII table in order to decrypt the file.
Encryption and decryption process involves generation of seed for RSA, AES and as well as the public and the private keys. To generate the matrices, a five digit magic sum as well as initial seed is provided as input. In addition to the magic sum, an initial starting value is also provided as input along with the file to be encrypted. The generated matrices are stored separately in a file. Decryption process is similar to the encryption process whose input is the intermediate file which is encrypted in the encryption process.

C. SOFTWARE DESIGN ALGORITHM.
The algorithm used for FTP is given below:

SERVER:
1. Initially server creates socket.
2. It then calls bind function to register itself to the kernel.
3. Next it calls listen function and waits for receiving the client connections.
4. This is followed by accept() system call which takes the first connection request on the queue and creates another socket with the same properties as the socket file descriptor.
5. Then the server accepts and processes. It will make the control connection.
6. The server is actively running, if any incoming connections are coming it will accept those by calling forking new child for each connection.
7. The file transfer takes place between client and server.
8. For each transfer data connection is opened and closed.
9. Lastly the server closes the connection when request completes.

CLIENT:
1. Initially the client also creates the socket using the socket system call.
2. It then calls the connect system call for establishing the connection to the server.
3. Authentication is done.
4. The file transfer takes place between client and server.
(using series of read and write operations)

D. DATA FLOW DIAGRAMS.
Since we are using model which is mainly mathematical in nature, with no multiple components, and hence there is no considerably complex flow of data between one component to the other. The only complexity comes in the exchange of the files between the two hosts. The algorithm essentially takes an input from the user, performs the necessary computations, and sends the encrypted file to the receiver.
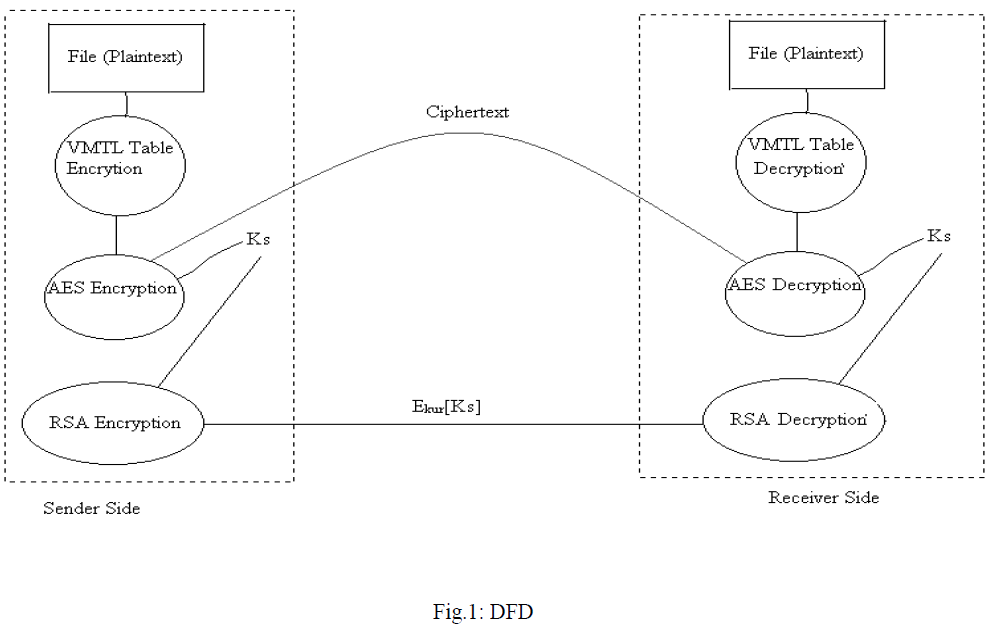image\

\E. ENCRYPTION.
The algorithm encrypts the message using AES first, and then the symmetric key using RSA.
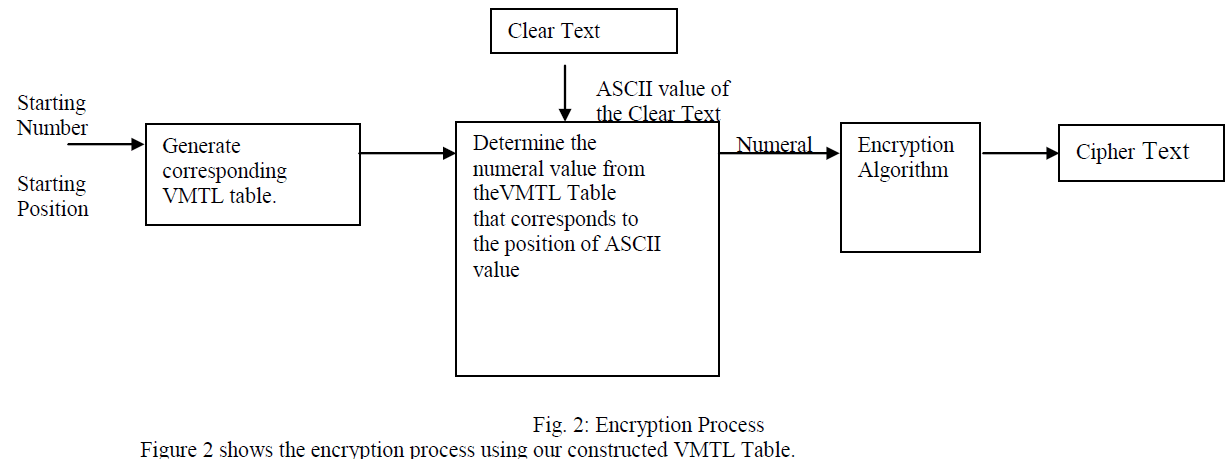image
1. Input the seed number which is a starting number for the VMTL table construction.
2. Parse the plain text letter by letter and divide it into blocks.
3. For each character, find out it‟s corresponding ASCII value using looping constructs to determine corresponding values of I and J for location of the corresponding values.
4. Once the VMTL Table is selected select the nth number in the VMTL Table where n is the ASCII value of the text.
5. Run the RSA algorithm on the chosen secret number.
6. Send the encrypted cipher text across the network to the receiver.
Man in the middle attack is hard to carry out as each character is encrypted using a different secret number each time.

F. FTP.
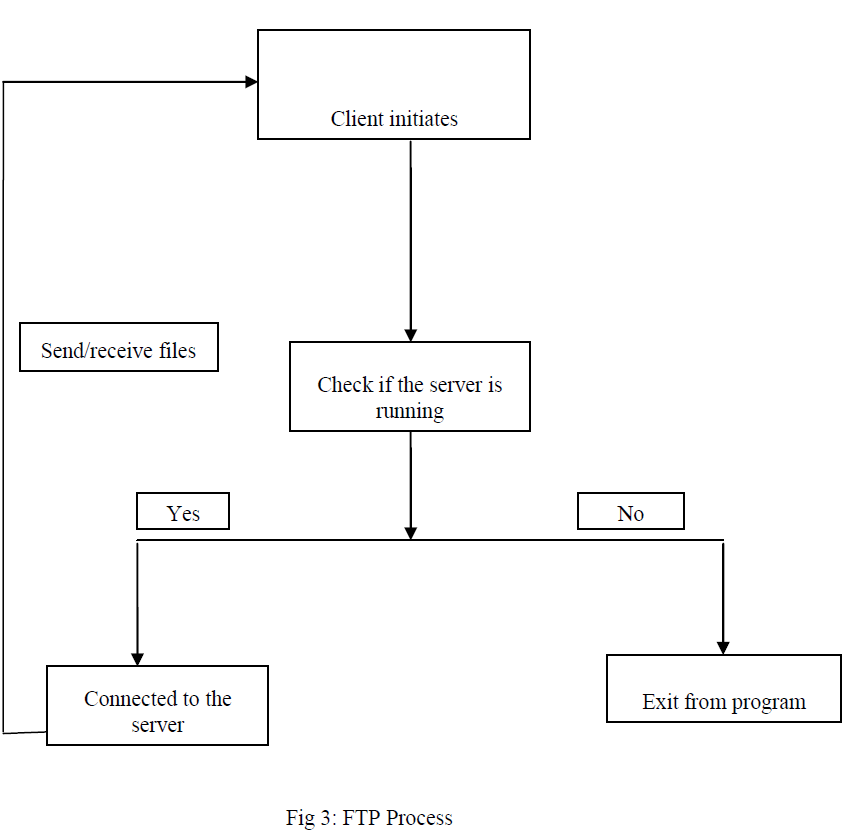image

ALGORITHM
SERVER:
1. Initially server creates socket.
2. It then calls bind function to register itself to the kernel.
3. Next it calls listen function and waits for receiving the client connections.
4. This is followed by accept() system call which takes the first connection request on the queue and creates another socket with the same properties as the socket file descriptor
5. Then the server accepts and processes. It will make the control connection.
6. The server is actively running , if any incoming connections are coming it will accept those by calling forking new child for each connection
7. The file transfer takes place between client and server
8. For each transfer data connection is opened and closed.
9. Lastly the server closes the connection when request completes
CLIENT:
1. Initially the client also creates the socket using the socket system call.
2. It then calls the connect system call for establishing the connection to the server.
3. Authentication is done.
4. The file transfer takes place between client and server.
(using series of read and write operations)

G. DECRYPTION.
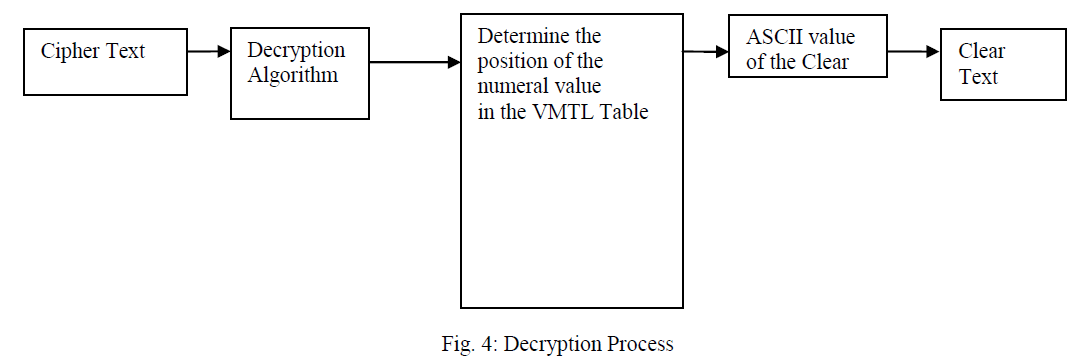image
Figure 4 shows the process for the decryption of the text with the different modules. It is just the reverse process of the encryption process.
1. Generate VMTL tables using the seed number and starting position.
2. Run AES algorithm on the cipher text.
3. Using the acquired number find out the actual ASCII value of the text based on it‟s position in the VMTL Table.
4. If the secret numeral is present at the nth position then n is the ASCII value.
5. Using this ASCII value find out the corresponding plain characters.

IMPLEMENTATION
The working methodology of the proposed add-on security model is discussed stepwise.
Create the VMTL Table using the starting point and the seed number.
To encrypt the character, use the ASCII value of the character to determine the numeral in the VMTL table by considering the position in it. Let NP and NC denote the numeral of the plaintext and cipher text respectively. Based on NP and NC values, all plaintext and cipher text characters are encrypted and decrypted respectively using AES algorithm.
Encrypt the symmetric key for the AES using RSA.
Append the encrypted key with the file and send it across the network.
To speed up the operations, perform them in parallel in a simulated environment. For that, use Maui scheduler with back filling philosophy.

A. VMTL Table and their construction
A VMTL table of order n is an arrangement of integers in an n x n matrix such that the sums of all the elements in every columns are equal. A normal magic square contains the integers from 1 to n2/2. It exists for all orders n ≥ 1 except n = 2, although the case n = 1 is trivial as it consists of a single cell containing the number. The constant sum in every row, column and diagonal is called the magic constant or magic sum, M. In [2, 5] the algorithms to construct magic square of order n and to construct VMTL of Kn are shown.

B. Encryption / Decryption of message using RSA and AES cryptosystem with VMTL Table
To show the relevance of this work to the security of public-key encryption schemes, a public-key cryptosystem RSA is taken. RSA was proposed by Rivest et al. The private key of a user consists of two prime p and q and an exponent (decryption key) d.
The public-key consists of the modulus n = pq, and an exponent e such that d = e-1 mod (p-1) (q1). To encrypt a plaintext M the user computes C = Memod n and decryption is done by calculating M = Cdmod n. In order to thwart currently known attacks, the modulus n and thus M and C should have a length of 512-1024 bits in this paper. In order to get a proper understanding, let p = 11, q = 17 and e = 7, then n = 11(17) = 187, (p-1)(q-1) = 10(16) = 160. Now d = 23. To encrypt, C = M7mod 187 and to decrypt M = C23mod 187.
Suppose the message is to be encrypted is “BABA”. The ASCII values for A and B are 65 and 66 respectively. To encrypt B, the numerals which occur at 66th position in the VMTL Table is taken. Thus NP(A) = 42 and 48, NP(B) = 36 and 44. Hence C(B) = 367mod 187 = 9, C(A)=427mod 187 = 15,
C(B) = 447mod 187 = 22,
C(A) = 487mod 187 = 157.
Thus, for same A and B which occur more than once, different cipher texts are produced for the same.
image

CONCLUSION
In this paper we proposed an alternative approach to existing ASCII based cryptosystem a number based approach is thought of and implemented. This methodology will add-on one more layer of security, it adds numerals for the text even before feeding into AES algorithm for encryption. This add-on security is built using VMTL position equivalent to the character to be encrypted. Further efficiency of cryptographic operation depends on performing them in parallel. Simulation using different number of processors for encryption /decryption has shown that the time taken for decryption is approximately 1.2 times larger than the corresponding time for encryption.

References
  1. J. Gallian, A dynamic survey of graph labeling, Electronic J. Combin., 14 (2007), DS6.
  2. Krishnappa.H.K., N.K.Srinath and P.Ramakanth Kumar, “Magic Square Construction Algorithms and Their Applications”IUP Journal of Comp.Maths, Vol.3, (2010), pp 34-50.
  3. Y. Lin and M. Miller, Vertex magic total labeling of complete graphs, Bull. Inst. Combin. Appl. 33(2001), 68-76.
  4. Krishnappa H K, Kishore Kothapalli and Venkaiah V Ch. (2009), “Vertex Magic Total Labelings of Complete Graphs”, AKCE Journal of Graphs and Combinatorics, Vol. 6, pp. 143-154.
  5. Krishnappa.H.K., N.K.Srinath and P.Ramakanth Kumar, Vertex Magic Total Labeling of Complete graphs, IJCMSA., Vol 4, No 1-2 (2010), 157-169.
  6. Gopinanath Ganapathy and K. Mani. Add-On Security Model for Public-Key Cryptosystem Based on Magic Square Implementation, Proceedings of the World Congress on Engineering and Computer Science 2009 Vol I ,WCECS 2009, October 20-22, 2009, San Francisco, USA.