Department of Statistics, Faculty of Social-Science, University of Botswana, Gaborone, Botswana
Received date: May 10, 2018; Accepted date: July 02, 2018; Published date: July 06, 2018
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
The objective of this paper is to provide an alternative distribution to the varieties of discrete distributions to be used to fit count data. We propose a compound of Generalized Negative Binomial and Shanker distribution, namely, the Generalized Negative Binomial-Shanker (GNB-SH) distribution. GNB-SH distribution can be used to fit count data while still maintaining similar characteristics as the traditional negative binomial. This new formulation is a generalization of new mixture distributions namely the Negative Binomial- Shanker (NB-SH) distribution and the Binomial-Shanker (BI-SH) distribution. Some mathematical properties of this distribution and that of its special cases are studied. Parameter estimation for GNB-SH and NB-SH distributions is also implemented using maximum likelihood.
Generalized Negative Binomial-Shanker (GNB-SH), Binomial-Shanker (BI-SH)
Most often, existing discrete distributions sometimes fail to fit count data well due to various reasons such variations within the data, the shape of the distribution and assumptions related to these distributions [1]. As a result, experiencing poor fit of existing discrete models in analysis of count data is a major concern in fields such as medicine, transport, engineering and agriculture. Therefore, researchers are striving to come up with new discrete distributions which could provide a better fit to the observed count data when compared to other existing models. For that reason, we propose the new distribution namely the Generalized Negative Binomial-Shanker (GNB-SH) distribution which is obtained by compounding the distribution of GNB (m,p,β), where p = exp(−λ) with distribution of SH(θ). The expectation is that GNB-SH distribution should provide a better fit to observed count data when compared to other competing distributions such as the traditional NB distribution.
Various researchers used the concept of mixing distributions to explore new flexible distributions that performs better than standard well known models. In many cases, mixed Poisson and Negative Binomial (NB) distributions usually provide better fit when compared to other existing distributions. When the data is over-dispersed, stands out to be the best the when compared to Poisson due to its assumptions flexibility. Based on this strategy of mixing distributions, various researchers were able to explore new flexible distributions.
Looking at previous researches, [2] mixed NB and Lindely distribution which have been extended and applied in many count data analysis [3-6]. Saengthong et al. obtained a mixture of NB and Crack distribution which contains three special cases namely Negative Binomial-Inverse Gaussian (NB-IG), Negative Binomial-Birnbaum-Saunders (NB-BS) and Negative Binomial-Length Biased Inverse Gaussian (NB-LBIG) [7]. These results were extended to make obtain a distribution suitable for zero inflated count data [8].
Gerstenkorn compounded the Generalized Negative Binomial (GNB) distribution and the Generalized Beta (GB) distribution which was later modified by Rashid et al. to study zero truncated count data [9,10]. Rashid et al. studied a mixture of Generalized Negative Binomial with Generalized Exponential (GNB-GE) distribution which entailed a mixture of Negative Binomial with Generalized Exponential (NB-GE) [11,12]. For its appealing performance, a zero inflation parameter was added to NB-GE distribution to make it more suitable for count data with excess number of zeros [13].
In mixtures related to Poisson distribution [14] introduced a mixture of one parameter Lindely distribution [15] with Poisson distribution. Some extensions and modification related to this formulation can be found [16-20]. Other Poisson mixtures include the Poisson-Shanker mixture [1], the Poisson- Amarenda mixture [21] and the Poisson- Sujatha mixture [22-25].
In this work, we present the concept of compounding distributions and the distributions involved in formulating GNB-SH distribution in Section 2. This section ends with mixing GNB distribution and Shanker distribution and provides its special cases. Section 3 entails mathematical properties related to this distribution including that of special cases. Section 4 deals with parameter estimation of NB-SH and GNB-SH using maximum likelihood. Section 5 presents the conclusion of this paper that includes our future plans.
Generalized Negative-Binomial Distribution
A discrete random variable X is said to be a Generalized Negative-Binomial (GNB) distribution if its pmf is given as:
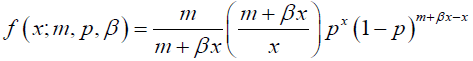(1)
for x = 0,1, 2, 3,……, and zero otherwise, where
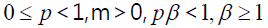(a)
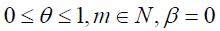(b)
When β = 0 & m∈N, the pmf of equation (1) reduces to Binomial distribution and when β = 1, equation (1) reduces to the pmf of NB distribution which its mean and factorial moment respectively are given as:
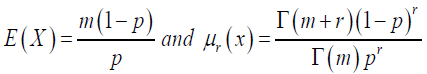(2)
where ᴦ (.) is the Gamma function, see [23-25]. In GNB distribution, the parameters m, pand β are constants but here it is assumed that where λ is a random variable following the Shanker distribution.
Shanker distribution
As an extension of Lindely distribution [15] Shanker (SH) distribution was proposed by Shanker [26] who also provided its mathematical properties. This distribution is a mixture of Exponential distribution with scale parameter θ and a Gamma distribution with shape parameter 2 and scale parameter θ. This distribution has shown a better fit when it was compared with Exponential and Lindely distribution in modelling of lifetime data. The density function of this distribution is given as:
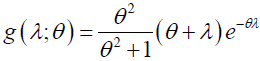(3)
for λ > 0 and zero otherwise, where θ > 0. Its moment generating function (mgf) is given as:
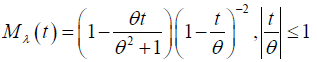(4)
Compound Distribution
According to the definitions provided by Gurland [27], Compounding of distributions occurs when all or some parameters of a certain distribution (Parent probability distribution) is treated as a random variable of another probability distribution called Compounding distribution. In compounding, the support of the Parent distribution determines the support of the compound distribution [27,28]. If the parent distribution is discrete (continuous), then the compound distribution will become discrete (continuous).
Compounding played an important role in revival of NB distribution which is a compound of Poisson distribution with its parameter λ treated as a Gamma variable. Considering the case of one discrete variable, the definitions and relations provided by Gurland [27] to compound a distribution are as follows:
Let X be a discrete random variable with f (X|λ)where parameter λ is a random variable with probability density function g(λ), then a compound distribution h(x) is defined as:
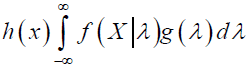(5)
Compounding of Generalized Negative-Binomial distribution with the Shanker Distribution
Definition: Let X be a random variable of a GNB-SH(m,β,θ) distribution denoted by X ~ GNB − SH(m,β,θ) when X has a GNB distribution with parameters m,β and p= e−λ where λ is distributed as SH with parameter θ >0 , i.e X|λ ~ GNB(m,β , p = e−λ) and λ ~ SH (θ).
Theorem: Let X ~ GNB − SH (m,β,θ) , then the pmf of X is given as:
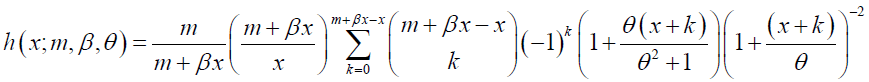(6)
for x = 0,1,2,3,…., and zero otherwise, where
0 ≤ p < 1,m > 0, p β < 1,β ≥1, θ (a)
0 ≤ θ ≤1, m∈N, β = 0, θ > 0 (b)
Proof: If X ~ GNB − SH (m,β,θ) defined in equation (1) and λ ~ SH (θ) defined in equation (3), then using equation (5), the pmf of X can be obtained by:
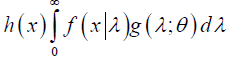(7)
Substituting p = e−λ in equation (1) we have f(X|λ) being defined as
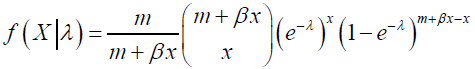
using binomial expansion we obtain
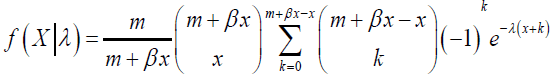(8)
By substituting equation (3) and equation (8) into equation (7) we obtain
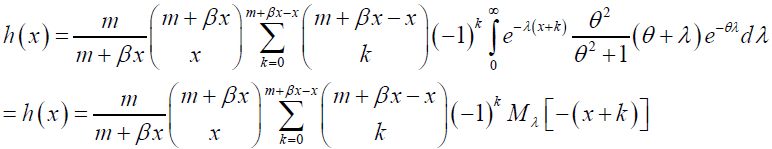(9)
Substituting the moment generating function of SH distribution in equation (4) into equation (9) the pmf of GNB − SH (m,β,θ) the distribution is finally given as
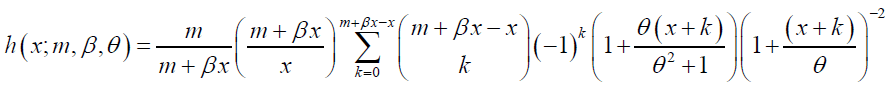
Next we provide the special cases of GNB-SH and their probability mass functions. Note that these special cases can simply be proven by substituting in the assumed values provided for each case.
Corollary: If β = 1, then the GNB-SH pmf in equation (6) reduces to a mixture of NB and Shanker distribution denoted as X ~ NB − SH (m,θ )with pmf
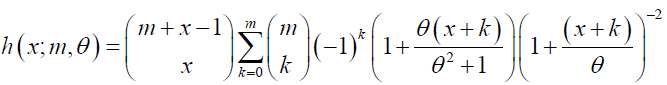(10)
Corollary: If β = 0 and m∈N , then the GNB-SH pmf in equation (6) reduces to a mixture of Binomial and Shanker distribution denoted as X ~ BI − SH (m,θ) with pmf
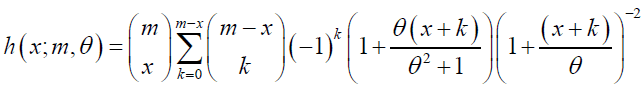(11)
This deals with provision of Factorial moments of the distributions. The ordinary (crude) moments of the GNB-SH distributions can be obtained by using the formula
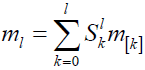
where Slk stands for the Stirling numbers of the second kind [29]. Therefore, only the factorial moments of the mixture of NB and Shanker distribution will be considered.
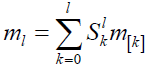
where Slk stands for the Stirling numbers of the second kind [29]. Therefore, only the factorial moments of the mixture of NB and Shanker distribution will be considered.
Definition: If X ~ NB − SH (m,θ) , then the factorial moment polynomial
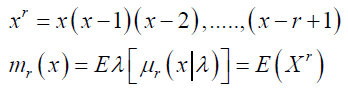
is called the factorial moment of order r of a mixture of NB with Shanker distribution (NB-SH), where μr (x|λ) is the factorial moment of NB distribution.
Theorem: The factorial moment of order r of NB-SH distribution is given by
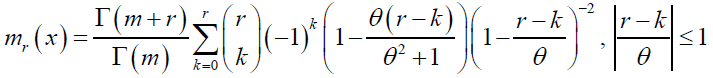(12)
for r = 1,2,3,…., where m, θ>0.
Proof: From the factorial moment of NB distribution in equation (2), if we let p = e−λ then the factorial moment of order r of NB-SH distribution is given as
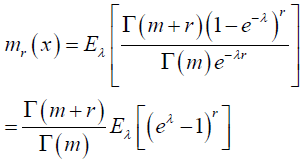
using binomial expansion we obtain
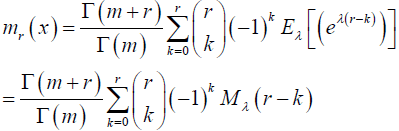
Substituting the moment generating function of SH distribution with t = r- k we get
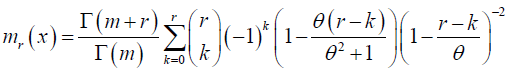
From the factorial moments of NB-SH distribution in equation (12), for convenience we let
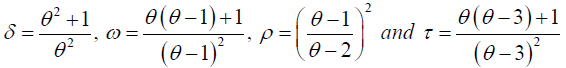
Then, the first four moments about zero are respectively given as
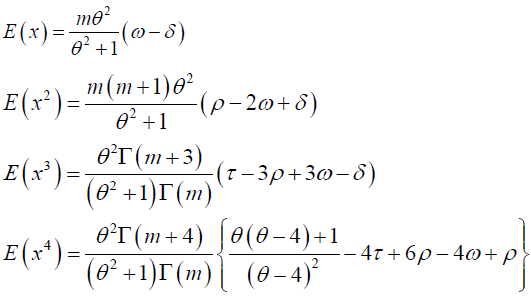
Definition: In this section, maximum likelihood is used to provide parameter estimates of GNB − SH (m,β,θ) distribution and that of its special case of NB-SH distribution (m,θ).
Estimation of GNB-SH distribution parameters using full likelihood function
Let X1,X2,X3,….,Xn a random sample of size n from the GNB-SH distribution with observed values x1, x2, x3,…., xn. We find the values of m, β and θ that maximizes the likelihood function (joint pmf of the sample) of GNB-SH. Parameter estimates can easily be obtained by maximizing the logarithm of the likelihood function with respect to m, β and θ as the product is replaced by the sums. Consider the likelihood function of GNB-SH distribution defined by
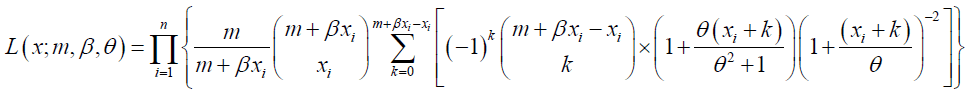
with corresponding log-likelihood function given as:
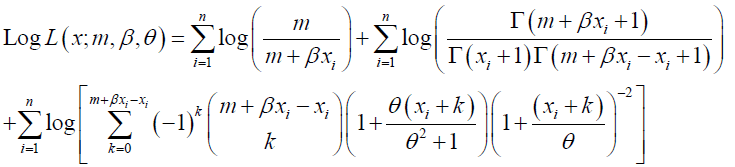
Maximum likelihood estimators of m, β and θ can be obtained by maximizing Log L (x; m, β, θ) with respect to m, β and θ respectively. That is
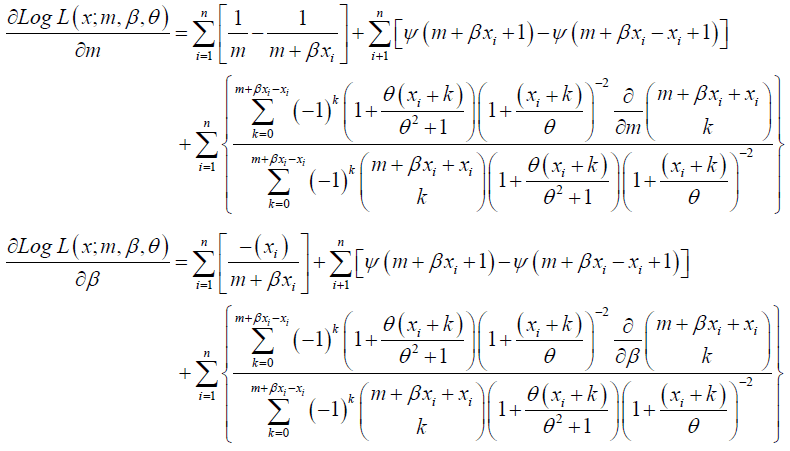
Estimation of NB-SH distribution parameters using full likelihood function
Consider the log-likelihood function of NB-SH distribution defined by
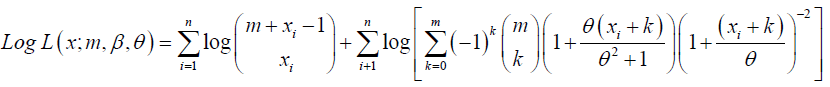
and the partial derivatives of this log-likehood with respect to m and θ are given as
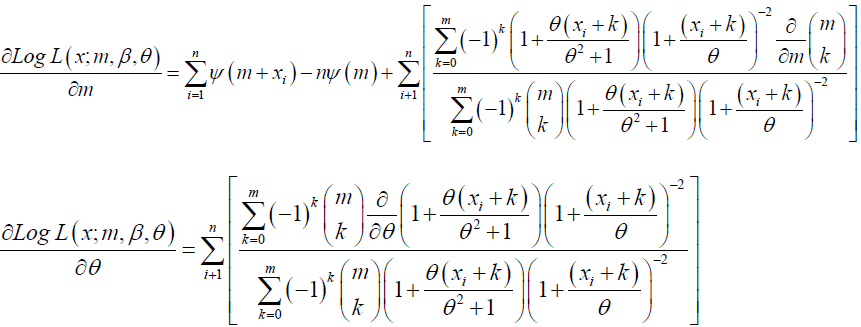
where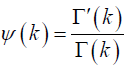 
is the digamma function [29,30].
The above derivative equations cannot be solved analytically, therefore we use Newton Raphson method which is a simple and powerful technique for solving equations numerically. Therefore, parameter estimates will be obtained by maximizing the loglikelihood function using a numerical iterative method.
This paper proposed a new distribution which was obtained by mixing GNB distribution with a shanker distribution. It was found that NB-SH and Binomial-Shanker distributions are its special cases. Some mathematical properties which relates to its special case was provided. Parameter estimation of GNB-SH and NB-SH using MLE. Finally, our future interest will be in comparing the efficiency of this distribution with that of Poisson and NB distributions using real data sets.
Menu