INTRODUCTION
|
| Recent technological advances in micro- electronic-mechanics (MEMs) and the low-power wireless communications have paved the way for the deployment of dense wireless sensor networks (WSNs). Such networks are expected to play an important role in a wide range of applications, including motion detection, environment monitoring, military surveillance and reconnaissance, etc. [1]. Mass production of low-cost sensors necessitates powering them with limited-energy, often non- rechargeable batteries [2]. This makes energy consumption a critical factor in the design of a WSN and calls for energy-efficient communication protocols that maximize the lifetime of the network subject to a given energy budget. |
| In this paper, we investigate the maximization of the coverage time for a clustered wireless sensor network by optimal balancing of power consumption among cluster heads (CHs). Clustering significantly reduces the energy consumption of individual sensors, but it also increases the communication burden on CHs. For this, our analytical models incorporate both intra- and inter cluster traffic. Depending on whether location information is available or not, we consider optimization formulations under both deterministic and stochastic setups, using a Rayleigh fading model for inter cluster communications. For the deterministic setup, sensor nodes and CHs are arbitrarily placed, but their locations are known. Each CH routes its traffic directly to the sink or relays it through other CHs. For the stochastic setup, we consider a cone-like sensing region with uniformly distributed sensors and provide optimal power allocation strategies that guarantee (in a probabilistic sense) an upper bound on the end-to-end (inter-CH) path reliability. Two mechanisms are proposed for achieving balanced power consumption in the stochastic case: a routing aware optimal cluster planning and a clustering- aware optimal random relay. For the first mechanism, the problem is formulated as a signomial optimization, which is efficiently solved using generalized geometric programming. For the second mechanism, we show that the problem is solvable in linear time. Numerical examples and simulations are used to validate our analysis and study the performance of the proposed schemes. |
DRAWBACKS OF EXISTING SYSTEM
|
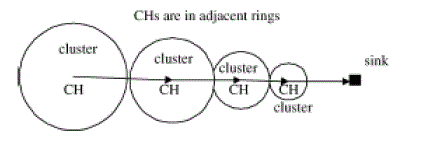
| For clusters with comparable area coverage and node density, the volume of intra cluster traffic is roughly the same for all the clusters. On the other hand, the traffic relayed by different CHs is highly skewed; the closer a CH is to the sink, the more traffic it has to relay, and thus the faster it drains its energy reservoir. Such an imbalanced power consumption situation is essentially caused by most of the many-to-one communication paradigm in WSNs that is the traffic from all the sensors is equally destined to the sink (see Figure.1). If we do not take measures to deliberately balance power consumption at different CHs, a “traffic implosion” situation will arise. More specifically, CHs that are closest to the sink will exhaust their batteries first. Reassigning sensors to the next-closest CHs to the sink will simply increase the energy consumption of these CHs. As a result, they will eventually be the second batch of CHs to run out of the energy. This process continues to the next level of CHs, propagating from inside out eventually leading to early loss of coverage and partitioning of the topology. |
PROPOSED SYSTEM
|
| Our goal in this paper is to design optimal power-allocation strategies that address this imbalance by maximizing the coverage time, defined as the time until the CH runs out of battery2 These strategies deliberately offset the impact of the skewed load by appropriately adjusting the transmission range (equivalently, transmission power, cluster size) of different CHs. Because the volume of relayed traffic is also affected by the underlying routing scheme, a joint routing/clustering algorithm design methodology is needed to achieve the power balance among the CHs. The additional energy consumption is attributed to the aggregation of intra-cluster traffic into a single stream that is transmit-ted by the CH and to the relaying of inter-cluster traffic from other CHs. Such relaying is sometimes desirable because of its powerconsumption advantage over direct (CH- to-sink) communication. Given the high density of sensors in common deployment scenarios (a density of 20 sensors per cubic meter is not unusual [1]); the traffic volume coming from a CH can be orders of magnitude greater than the traffic volume of an individual sensor. Even though the CH may be equipped with a more durable battery than the individual sensors it serves, the large difference in power consumption between the two can lead to shorter lifetime for the CH. Once the CH dies, no communications can take place between the sensors in that cluster and the rest of the network. |
MAIN CONTRIBUTIONS
|
| The Main Contributions Of This Paper Are As Follows. First, In Contrast To Previous “Load-Balanced” Algorithms, We Pro-Vide “Power-Balanced” Alternatives That Aim At Directly Optimizing Coverage Time By Accounting For The Interaction Between Clustering And Routing, I.E., Simultaneously Taking Into Consideration The Impacts Of Both Intra- And Inter-Cluster Traffic. Second, In Contrast To Previous Algorithms, Which Are Based On Heuristics, Ours Is Based On An Analytical Approach In Which Coverage- Time Maximization Is Formulated As A Signomial Optimization Problem That Can Be Efficiently Solved Using Generalized Geometric Programming (GGP) [22,23]. Our Analysis Guarantees An Upper Bound On The Path Reliability For Communications Between The Originating CH And The Sink Node. Two Schemes Are Proposed For Achieving Power- Balanced Communications: Routing-Aware Optimal Cluster Planning And Clustering-Aware Optimal Random Relay. Numerical Examples And Simulations Are Used To Validate Our Analysis And Compare Our Proposed Schemes With Pure “Load-Balancing” Algorithms. Our Results Indicate That By Accounting For The Interaction Between Clustering And Routing, The Proposed Schemes Achieve A Significant Reduction In Energy consumption and an improved coverage time for the two considered network models. |
SYSTEM MODELS
|
| A. Network Model |
| We consider a WSN that consists of two types of nodes: Type-I and Type-II nodes. Type-I nodes, which are called sensing nodes (SNs), are responsible for sensing activities. Such nodes are small, low cost, and disposable. They can be densely deployed across the sensing area. Neighboring SNs are organized into clusters. A Type-II node has a more powerful energy source and a stronger computing capability and is designated as CH. Type- II nodes are responsible for receiving and processing the sensing outcomes of SNs. A CH may collect data from intra cluster SNs, conduct signal processing on these raw data to create an application-specific view of the cluster, and then relay the fused data to the sink through intermediate CHs. The availability of location information is an appropriate assumption in many applications of WSNs(e.g., static WSNs in open regions). It can also apply to networks where sensors are first randomly deployed but later their locations become known, for example, through GPS- assisted mechanisms. Each sensing node (for brevity, a sensor) is assigned to one CH. The sensor generates traffic at an average rate of λ bits/sand sends it to its CH, which in turn delivers it to the sink directly or through other CHs(see Fig. 1). |
| We assume that each sensor has sufficient energy to communicate directly with its CH. This could be done by either transmitting at a high enough transmission power or using a low enough transmission rates (and thus a longer duration for each transmitted bit). Furthermore, we assume that the CH depletes its energy at a much faster rate than the sensors it serves. This assumption is justified by the low data rate and duty cycle of commonly used sensors (i.e., for most of the time, the sensor is put to sleep, in contrast to the CH, which is active most/all the time). Accordingly, we focus our attention on energy depletion at CHs. From a strategic point of view, a CH is more critical to the coverage of the network than individual sensors. |
| We consider a cone-like sensing region Ψ of radius R and angle φ. The sink is located at the vertex, as shown in Figure 2.The region Ψ may either be an isolated sensing field or a part of a larger sensing field of a general shape (see remark later in this section). The cone-like geometry, albeit idealistic, serves as a basis for understanding the intrinsic tradeoffs involved in a joint clustering/routing optimization framework. In addition, it still captures the fundamental traffic- implosion phenomenon in general WSNs. It has been widely used in the analysis of sensor networks. For example, a circular region (which is a special case of a cone) was recently used in [23], [11]. Sensors are uniformly distributed across Ψ with density ρ. Due to energy considerations, only those sensors within distance r0 from the sink can communicate directly with the sink; all other sensors are organized into clusters and they communicate their data through their respective CHs. Like many distancebased (or equivalently, received-signal-strength-based) cluster formation algorithms, we assume that each CH is located at the center of its cluster. |
| B. Channel Model |
| We use a Rayleigh fading model to describe the channel between two CHs and also between a CH and the sink. At a transmitter–receiver separation, the channel gain is given by |
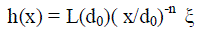 |
| Because ξ is random, the received signal is also random. Hence, correct reception of a signal can be guaranteed only on a probabilistic basis. In our work, we require that Pr{er ≥τ} ≥ δl for reliable reception, where er is the energy of the received signal, τ is a predefined energy threshold, and δl is the required link reliability. For an end-toend path of M links that experience independently and identically distributed fades, the overall path reliability, i.e., the probability of a successful end-to-end reception, is given by Mδp = δl . |
| Therefore, in order to guarantee path reliability the link reliability δl should be at least δp. The assumption of link fading is justified by noting that the distance between consecutive CHs is much larger than the wavelength of the carrier for a system operating at 2.4 GHz, which is a typical value in current standards. |
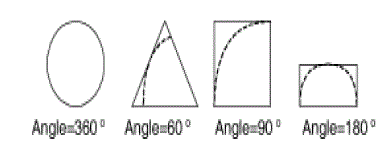
| Remark: Although our model assumes a cone-like sensing area and a two-tier network structure, the analysis adequately captures the intrinsic interaction between inter- and intra-cluster traffic. In addition, we note that this cone shape is general enough to approximate many other shapes. For example, as shown in Figure 3, a cone can approximate the shapes of circle, triangle, square, and rectangle, respectively, when the angle φ is properly set. The analysis can also be extended to handle a non- regularly-shaped region by covering it with a series of element shapes that can be approximated by cones, similar to the approach used in cellular networks(in cellular networks, the region is approximately covered by hexagons). A multi-layered organization of sensors, such as the “spine” hierarchy [12], can also be accommodated in our analytical framework. In this case, our analysis provides the optimal CH coverage time for the “base” layers and a sub-optimal coverage time for the whole network. The details of such extensions are beyond the scope of this paper and will be considered in a future work. |
PROPOSED MODEL SCHEMES
|
| A. Clustering Algorithm |
| Let co= (co 1,…co N) be the resulting optimal clustering vector. For i=1,2,3,….N, CH i is assigned Mo i = co i/λ sensor nodes. Node assignment is done as follows. Sensor nodes are considered sequentially, one at a time. A given sensor is assigned to the closest CH, say i, provided that the number of assigned sensors to CH does not exceed. If it does, then the next closest CH is considered, and so on. A pseudo code of the algorithm is given in Table I. Note that depending on the order in which sensors are considered in the algorithm, different assignments (clusters) may be produced. These assignments achieve the same coverage time, i.e., each of them minimizes the maximum power consumption among CHs. However, they differ in the total energy consumption of individual sensors. |
| The algorithm can be easily refined to reduce the total sensor-energy consumption of the initial node assignment. This is done as follows. First, we use the algorithm in Table I to produce an initial assignment. Such an assignment is optimal with respect to (11) but is not necessarily unique. Then, we consider swapping the cluster assignment of all pairs of sensors that belong to different clusters if this swapping results in a reduction in the total sensor- energy consumption in the network. Note that such swapping does not change the energy consumption of the corresponding CHs. |
| For each sensor in the first initial cluster, the number of pairs to be considered for swapping is, for a total off or all the sensors in the first cluster. A simple combinatorial argument shows that the total number of pairs to consider is bounded by, which is of low complexity. |
| Algorithm Output |
| We use the following example to illustrate the above node swapping process. Consider a network of 3 CHs (CH1, CH2, CH3) and 4 SNs (A, B, C, D). For SN X, we use the triple (i, j, k) to indicate the per-bit energy consumption of node X when X is assigned to one of the three CHs. For example, B (2, 4, 1) means that SN B requires 2, 4, and 1 Joules/bit to communicate with CH1, CH2, and CH3, respectively. Suppose that the per-bit energy consumptions of various SNs are: A(3, 4, 5), B(2, 4, 1), C(1, 3, 1), and D(2, 5, 4). Suppose that to achieve optimal clustering, CH1, CH2, and CH3 should be assigned 2, 1, and 1 SNs, respectively. According to the sequential node assignment procedure, the initial node-to-CH assignment is given by {A, C} → CH1, {D} → CH2, and{B} → CH3, yielding a total energy consumption of 10Joules/bit. Now, we conduct node swapping between CH1 and other CHs. Four possible assignments can result from such swapping, as shown in Table II. |
| B. Routing-Aware Optimal Cluster Planning |
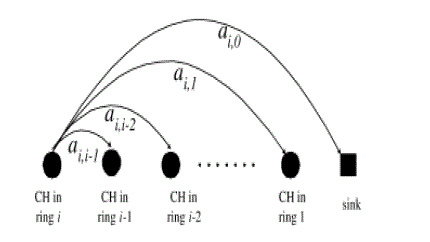
| Shortest-Distance Relay: In this scenario, traffic is relayed through the closest CH in the adjacent ring towards the sink. More specifically, a CH in the ith ring receives traffic originating from its own cluster as well as traffic relayed from CHs in the (i +1)th ring, and forwards the combined traffic to the closest CH in the (i − 1)th ring. Relaying continues hop-by- hop until the sink is reached. For the shortest- distance relay, we consider a routing-aware clustering mechanism that balances power consumption at different CHs. |
| Random Relay: In this scenario, a CH has the freedom to relay its data to the closest CH in any of the inner rings (this also includes the case of sending data directly to the sink).Let αij be the fraction of the load that a CH in the ith ring transmits to the closest CH in the jth ring, where 0 ≤ j < i and j = 0 denotes direct transmission to the sink. where the ith row of A represents the probabilities for relaying a packet at the ith ring to the closest CH in rings 0, 1, . . i − 1. The matrix A plays a critical role in balancing power consumption at different CHs. For example, increasing αij will reduce the relayed traffic carried by all CHs in rings j + 1, j + 2, . . . , i − 1. But this comes at the expense of higher power consumption at the CHs in the ith ring. ). By deliberately adjusting the relay probabilities at different CHs, a more balanced power consumption at different CHs can be achieved. |
| C. Routing-Aware Optimal Cluster Planning Scheme |
| Under this routing scheme, a CH in the ith ring transmits all of its data to the nearest CH in the (i − 1)th ring. Let xi be the physical distance between these two CHs. The expected transmission power is given by |
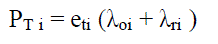 |
| where eti is the transmission energy per bit for the under-lying CH. The expected communication power consumption of any CH at ring i is given by |
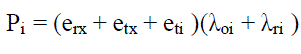 |
| Given eti, the corresponding received energy eri is given by |
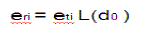 |
| The link-reliability requirement can be expressed as |
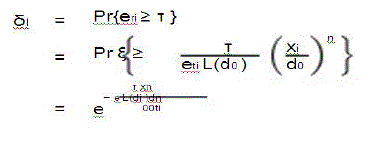 |
| Clustering-Aware Optimal Random Relay Scheme |
| Under random relay routing with i ≥ 2, the average power consumed to transmit data from any CH in the ith ring |
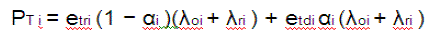 is is |
| where etri and etdi are the transmission energy per bit for relaying traffic to the nearest CH in ring i − 1 and for direct transmission to the sink,respectively. etri and etdi are derived as follows: |
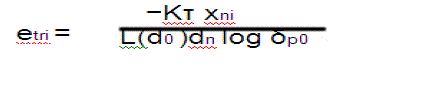 |
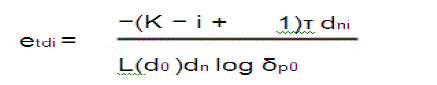 |
| these optimal values to drive the simulations of the two proposed schemes. Our main performance metric is the maximum expected power consumption of a def CH, Pmax = max {P1 , . . . , PK }. The smaller the value of Pmax , the longer is the coverage time. We set the radius of the circular sensing region to R =200 meters. Sensors are uniformly distributed throughout this region at density ρ = 1, i.e., the number of sensors in any area S follows a spatial Poisson distribution with parameter ρS. The number of CHs Kin both the analysis and the simulations is set to i=1 Ni , where Ni is obtained from (23) and K is given. The location of these CHs is also taken to be the same for the analysis and the simulations. However, in the simulations, clusters are not necessarily circular, and the notion of rings is not strictly followed. Instead, each sensor in a given simulation run is assigned to the nearest CH. As a result, two CHs that have the same distance to the sink may have different cluster sizes. Each sensor generates data according to a Poisson process of rate λ = 10 bits/seconds . Because of the randomness in the traffic and node locations, the powers consumed by different CHs that have the same distance to the sink may be different in the simulations. In this case, Pmax is taken as the maximum. |
| For the first ring, there is no difference between relaying to the next CH and directly communicating with the sink. Therefore, |
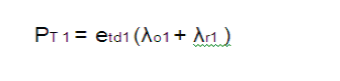 |
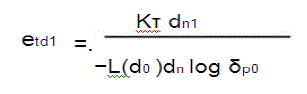 |
NUMERICAL RESULTS AND SIMULATIONS
|
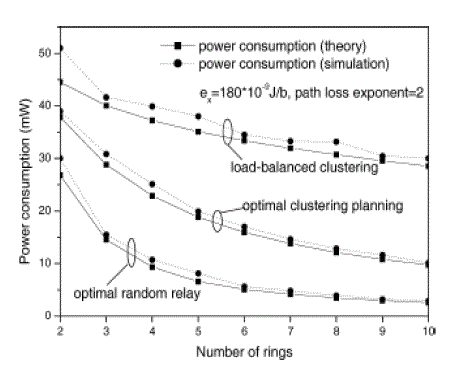
| We now consider the stochastic scenario for a circular (φ = 360o ) sensing region. We study the performance of the optimal cluster planning and optimal random relay schemes, and contrast them with the LB clustering approach. To get a clear picture of the advantages of adjusting the routing parameters, we use LB clustering for the random relay scheme. To validate the adequacy of our analytical results, we contrast them with simulations conducted under a more realistic setup (explained below). For the two proposed schemes, we use the analytical results to compute the optimal radius profile ro and optimal relaying matrix Ao. We use Figures 7 depict Pmax versus the number of rings (K) for two path loss factors: n = 2. The transmitplus- defective per-bit circuit energy is set to ex = etx + erx = 180nJoule/bit. It is observed that the gap between the (approximate) analytical results and the simulations is reasonably small for all examined schemes, with the simulation results being slightly more conservative than the analysis. The disparity between the two is attributed in part to the approximate nature of the analysis and in part to the randomness in the packet generation process and the distribution of sensors within a CH. When n = 2, both the optimal cluster planning and the optimal random relay schemes result in significantly longer coverage times (smaller Pmax values) than the LB scheme. This phenomenon can be explained by comparing the optimal relaying matrices for n = 2 and n = 4. An example of these relaying matrices when K = 5 is listed below. It can be observed that when n = 4, the optimal random relay scheme prefers to relay most traffic to the CHs in the next ring towards the sink (the values along the diagonal of Aon=4 are close to one). This is because now the total power consumption is dominated by the transmission power (PT i), which is highly nonlinear in the transmission distance. As a result, for the random relay scheme, only a small portion of the traffic at each CH is transmitted across intermediate hops; the rest is sent hop-by-hop, making the scheme’s behavior quite similar to the LB scheme. Therefore, when n is large, the flexibility in choosing the nexthop CH offers little performance benefit. |
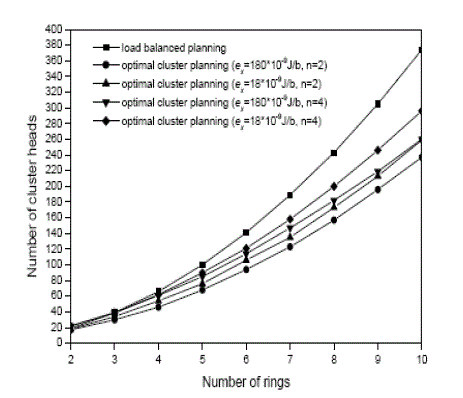
| Figure 9 depicts the total number of formed clusters K( i=1 Ni ) versus the number of rings (K) for the optimal cluster planning and the LB schemes. In addition to achieving a lower Pmax value (longer coverage time), optimal cluster planning also results in a smaller number of clusters, and hence reduced network-management overhead. |
CONCLUSIONS AND FUTURE WORK
|
| We considered the problem of coverage- time optimization by balancing power consumption at different CHs in a clustered WSN. Stochastic as well as deterministic network models were investigated in our analysis. Our study demonstrates the significance of simultaneously accounting for the impacts of intra- and inter-cluster traffic in the design of routing and clustering strategies. For the deterministic-topology scenario, we presented a joint clustering/routing optimization based on linear programming. For the stochastic scenario, two mechanisms for balancing power consumption were studied: the (routing-aware) optimal cluster planning and the (clustering-aware) optimal random relay. The control parameters in both mechanisms (radius profile and relay probabilities) were optimized with respect to the maximum power consumption of a CH. The optimization problems were formulated as signomial optimizations and linear optimization, which were efficiently, solved using generalized geometric programming and linear programming, respectively. For tractability purposes, our analysis for the stochastic model is necessarily approximate, as it relies on several simplifying assumptions. Simulations were conducted to verify the adequacy of this analysis and demonstrate the substantial benefits of the proposed schemes in terms of prolonging the coverage time of the network. For simplicity, in our simulations we assumed a TDMA-like MAC. The implications of various types of MACs (e.g., CSMA/CA, TDMA, hybrid TDMA/CDMA, etc.) on our algorithms is an important issue and will be investigated in our future work. We will also consider extending the analysis to hierarchically clustered WSNs (e.g., the “spine” hierarchy). |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
|
References
|
- F. Akyildiz, W. Su, Y.Sankarasubramaniam, and E. Cayirci, “A survey on sensor networks,” IEEE Communications Magazine, pp. 102-114, Aug. 2002.
- J. M. Kahn, R. H. Katz, and K. S. Pister, “Next century challenges: mobile networking for smart dust,” in Proc. ACM/IEEE MobiCom ’99 Conf., pp. 271-278, 1999.
- D. J. Baker and A. Ephremides, “The architectural organization of a mobile radio network via a distributed algorithm,” IEEE Transactions on Communications, vol. 29, no. 11, pp. 1694-1701, Nov. 1981.
- Ephremides, J. E. Wieselthier, and D. J.Baker, “A design concept for reliable mobile radio networks with frequency hopping signaling,” Proceedings of the IEEE, vol. 75, no. 1, pp. 56-73, 1987.
- R. Lin and M. Gerla, “Adaptive clustering for mobile wireless networks,” IEEE Journal on Selected Areas in Communications, vol. 15, pp. 1265-1275, Sep. 1997.
- M. Gerla and J.T.C. Tsai, “Multicluster, mobile, multimedia radio network,” ACM/Baltzer Journal of Wireless Networks, vol. 1, no. 3, pp. 255-265, 1995.
- J. Wu and H. L. Li, “On calculating connected dominating set for efficient routing in ad hoc wireless networks,”Proc. of the 3rd ACM International Workshop on Discrete Algorithms and Methods for Mobile Computing and Communications, pp. 7-14, 1999.
- F. Kuhn, T. Moscibroda, and R.Wattenhofer, “Initializing newly deployed ad hoc and sensor networks,” Proc. ACM MobiCom’04 Conference, Philadelphia, Sep. 2004.
- P. J. Wan, K. M. Alzoubi, and O. Frieder, “Distributed construction of connected dominating set in wireless ad hoc networks,” Proc. IEEE INFOCOM Conference, New York, June 23-27, 2002.
- W. B. Heinzelman, A. P. Chandrakasan, and H. Balakrishnan, “An application-specific protocol architecture for wireless microsensor networks,” IEEE Transactions on Wireless Communications, vol. 1, no.4, pp. 660670, Oct.2002.
- G. Gupta and M. Younis, “Load-balanced clustering of wireless sensor networks,” in Proc. IEEE InternationalConference on Communications (ICC’03), vol. 3, pp. 1848-1852, May 2003.
- D. Amis and R. Prakash, “Load- balancing clusters in wireless ad hoc networks,” in Proc. 3rd IEEE Symposium on Application-Specific Systems and Software Engineering Technology, pp. 25-32, Mar.2000.
- D. Amis, R. Prakash, T. H. P. Vuong, and D. T. Huynh, “Max-min d-cluster formation in wireless ad hoc networks,” in Proc. IEEE INFOCOM 2000 Conf., vol. 1, pp. 32-41, Mar. 2000.
- F. Chiasserini, I. Chlamtac, P. Monti, and A. Nucci, “An energy efficient method for nodes assignment in cluster-based ad hoc networks,” ACM/Kluwer Wireless Networks Journal (WINET), vol. 10, no. 3,pp. 223-231, May 2004.
- S. Bandyopadhyay, E. J. Coyle, “An energy efficient hierarchical clustering algorithm for wireless sensor networks,” in Proc. IEEE INFOCOM 2003 Conference, vol. 3, pp.1713-1723, Mar. 2003
|