Keywords
|
| Spatial Data Mining, Temporal Mining, Spatial knowledge, Collocation, Geographic Information System. |
INTRODUCTION
|
| In general, the representation of rules that are in the subject of data mining contains various syntactic and semantic significances. Modelling a rule definition is another important task for the data miners to bring back the emerging needs of the trends that are detected from the large spatial databases. There is lot of vagueness in defining the structures for the spatial data sets and the spatial related data sets. Reasons can be anxious from different directions of unavailability of super infrastructures, defining exact structure means making the spatial data more popular, and other defense restrictions. These reasons may look out as limitations or other way of preserving security for the data, instead of established seamless communication between one GIS to another. |
RELATED WORK
|
| A geographic information system is an information system for data representing aspects of the surface of the earth together with relevant facilities such as lakes, houses, and roads. A geographic database provides spatial and nonspatial information. In the developing era of GIS and mobile communities, it is very essential to integrate several GIS societies. For globalization of several spatial domains and to restructure them all as a global spatial domain, it is very essential to heighten the abstraction of some good structure that can be easily followed into programming languages as a type of data. A type is definitive reasoning system generally, the program deviation for a mining problem can be assumed as polytypic, if some of the parameters are data types. Polytypic program deviations necessitate a general noninductive definition of ‘data type’. A definition: a data type is a relator that has membership interferences that can be suggested. The definition throws much light on how the various other properties that are shared by all data types influence the definition of the collocation type. In particular, case of databases, all the data types must have the unique strength and all natural transformation between data types is strong [1]. |
| Many aspects of data types design deal with the problem of non-determinism, but ultimately they lay at the concepts of functors called relators. A functor is a constructor for a data type. A relator is which that can establish monotonic link between different facets of data types. The notion of membership has been examined in several experiments of the spatial data and the representation of the collocation erstwhile. During the course of inspection of data structures, it is not only the way to describe the ability of designing data type rather understanding the elementary aspects. This leads up to investigation of fans for the data types and it turns out that any relator with membership also has a unique fan. The definition of strong functors lead to the notion of data types what really the category theorists are working for the investigation. Contextually the technique of collection of several fan elements are grouped into a single common concept, which can be viewed as a single entity and nonessential information ignored – the abstraction [52]. |
THE ACTUAL DIFFERENCE
|
| The important and ragy (tr. rage) need to define the data type or data structure for storing the collocation rule is the concepts of variations (but not non-stability). The variation in the collocation is nothing but the change of intensity of the features that form as its core pattern. With regard to several changes occurred in a spatial domain the features form collocation, or could be resolved to form other new pattern or patterns. The direction of the inference changes as the changes occur to the features. Thus, this paper also strongly proposes a rule: change of gravity in the collocation. |
| A general definition for a collocation is proposed in [2][3][4] as a collocation is a subset of Boolean spatial features. |
A collocation rule is of the form: 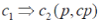 where c1 and c2 are collocations, p is a number representing the prevalence measure, and cp is a number measuring conditional probability. where c1 and c2 are collocations, p is a number representing the prevalence measure, and cp is a number measuring conditional probability. |
| According to normal spatial association rule, the identification of change of gravity may be considered as the confidence of that particular spatial item in the spatial item set that expresses equivalent to the features of a collocation [5][6][29]. A spatial association rule is a directional sign given to infer the basic characteristic, but a collocation rule could be a pattern that maps to a selected layer or layers of a spatial zone. The spatial association rule depicts the idea of relationship between reference objects of the spatial zone [5]. The collocation rule in its form gives a multidimensional or un-directional gravity identified structure. Representing a collocation rule requires a structure that can adapt to the changing position of gravity among the selected set of features in it [1]. |
Change of Gravity
|
| Change of collocation, a pattern style representation of collocation rule contains a set of features that have various weights. The features exist in the pattern, add up and become new features or vanish as they become obsolete for knowledge representation. However, the existing and emerging features should compete with appropriate weights to survive in the pattern that which will contribute the quality for the knowledge representation. The gravity for the pattern is observed to be as the feature that has obtained more weight in the pattern. In the natural spatial domain, the features obtaining the weights and losing the weights or features losing the weights less than the threshold which leads to their disappearance is a common phenomenon. |
Syntax Modelling
|
Syntax of a type can be developed and represented by canonical symbols that exhibit the storage and functional significance of a type. Let for F denotes a functor and S denotes a structure, then F and S should be relative in all aspects. F and S determine the functional aspects and the structural aspects of a type respectively. The proposed concept is supported by a data structure, where it can be abstracted and built as Object Type of Object-Oriented Paradigm. For given problem of spatial domain S, let W be the type that is used to identify the collocation pattern. S contains several forms of collocation patterns (W), which can represent different expressions of spatial knowledge. The sum total or the total glimpse of knowledge 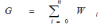 (G) in the problem spatial domain can be represented as: (G) in the problem spatial domain can be represented as: |
| W is defined to be the collocation pattern which is defined by a set of features. The features of a collocation are said to be organized is this experiment in two subjective components i.e., feature type and feature set. The feature type describes the structural details of the feature. The feature set describes the value details of the feature. For example if a collocation pattern that explains about some subject of spatial object is represented by Wi, containing k features, then the features among them will be f0 to fk, where k weighted features can make one collocation stand as Wi. Each fm is carefully expressed by feature type and feature set. Feature type of feature fm may be represented by fm(T) and feature set of feature fm is represented by fm(S). According to the basic programming conventions the fm(T) can be defined as any abstract collection type that can be directly or indirectly fit into the programming definitions like array, list, stack, queue, set, etc,. The fm(S) can be defined as any set of data that is consistent enough to express the idea and the attribute domain of the feature type. The need of representing feature as a member in the collocation like this can represent the knowledge. As a general procedure of data mining, converting the conventional data items into data sets or item sets is a general practice considered in designing the structure as a strategic weaving style. The most conventional style for representing the feature of the collocation is like template in C++. The selection of the fm(S) and the fm(T) for a feature are due to the natural phenomenal change in the spatial domain. As they change naturally, the importance of features varies temporally and thus the weights for each feature vary, which are naturally selected have indispensability and interdependency in the collocation. The need of integrated structure which encompasses the basics of collocation and their qualities is very essential for GIS. |
| A weight graph would be a better structure to represent the collocation, with an exception of weight represented in the vertices than the edges. The structure considered in this paper can be called as principal-ranking structure, a simple derivative of weight-vertex graph. Generally the weight graph has more concern about the weights of the edges, which is much bothered about the shape of graph. But in this context the shape is secondary; the importance is stressed much upon the existence of the vertex/node in the graph and its connectivity. The vertex-weight graph does not contain any directional representations. The number of nodes that are connected in the graph is the matter of apprehension which indicates the number of features that subsist in a collocation, rather how far or near they are arranged that proposes the shape.[5][6]. |
For assumed graph G, the notation is generally expressed as G = (V, E). Let G be a weight graph. The length of a path P is the sum of the weights of the edges of P. That is, if P consists of edges e0, e1, … ek-1 then the length of P, is denoted w(P), is defined as 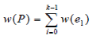 |
| But in the vertex-weighted graph the length is not the constraint, each vertex is assigned with a weight. The quantity of weight of a particular vertex is measured based on the importance of the feature in the pattern that is mostly deduced from the natural and temporal factors. |
COMPLEXITY AND EVALUATION
|
| The space complexity of graph is typically observed by expressing the complexity at each vertex bearing weights that represents candidate feature types, considering the direction of the connection of the vertices with least complexity. In the data-type, principal-ranking structure that is illustrated in this paper, the feature types become as collection of data, a collection type is classically experimented. Each of the collections is responsible for the connectivity of the dependent feature type collections. The overall design systematically can be observed as a fanned out dependent feature types with the more dominant feature types. |
| The type suggested experimentally can contain one or a set of dominant feature type collection in the core, and the other dependent feature types surrounding to the core, like a star. The star is mandatory to be observed that will identify the permanent feature type of the spatial object, which will be an important feature of the collocation. If a feature is installed in the centre of the type, in case of single existence of the feature it will act as an intelligent key feature for the collocation, which may also be brought from the original data source. In case of multiple existence of the feature, the set of the features will become as the facts for the collocation, which contain all naturally formed feature types, the intelligent keys again. |
| The principal-ranking structure (star-hierarchy structure) is a combination of basic B-Tree-like and Graph-List. The nodes of the star-hierarchy structure that represent the weighted-vertex-covers contain list of features sorted, The further level of nodes in the star-hierarchy structure are set-covers, contain vertex elements representing features, may be sorted according to the category of the set-covers’ [6][7][8][9]. But the overall structure of star-hierarchy is not necessarily constrained as sorted structure like B-Tree. The algorithmic complexity of the star-hierarchy structure is evaluated for each node and section of the structure discretely. At first-level, the weighted-vertex-covers, contains the features represented as base vertices, bear complexity as of a normal list. Similarly the vertices in the set-covers also bear complexity of a list. The classical and composite structure of the type described in this paper contains a list with several B-Tree nodes. The time complexity of the structure is evaluated by understanding the traversal of a list and a B-Tree. The general time complexity of a list containing k nodes will be O(k). The general time complexity of the B-Tree is said to be as the inequality h<=log (m/2)((n+1)/2). That is for m nodes, h height and n elements in each node. Where the complexity of the total structure becomes as O(k)+k(log(m/2)((n+1)/2)). However the complexity of the list is within the limits of complexity of total set of trees available in the structure it is negligible and hence the complexity can form as k(log(m/2)((n+1)/2)). |
According to [57][58] and other related [52][59[60][61][62][63] the concept of vertex cover applies appropriately. The vertex cover forms as the centrally installed set of vertices which represents the collection of the intelligent keys which are key feature types. Considering any heuristic graph, a collection of vertices representing the spatial objects and their features, a vertex cover of a graph is observed, a set of vertices that contains at least one end-point of each edge. A completely undirected graph is phenomenal representation of the geographical space. A vertex cover from the undirected graph is a subset 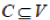 such that for all such that for all 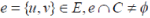 . The vertex-cover, problem resolves in finding the value that is the size of the cover |C|. . The vertex-cover, problem resolves in finding the value that is the size of the cover |C|. |
| The data mining aspect of the graph theory persevere in designing the structure of the knowledge; approximating the covers from the graph is measured akin to the mining of rule and forming a structure. The approximation is most naturally (a heuristic) a greedy algorithm which repeatedly selects an edge that has not yet been covered, and places one of its end points in the current covering set. Typical approximating routines are as follows. [6][7][8][9][10]. |
 |
| 3. return C. |
| The Weighted-Vertex-Cover, determines the ultimate set of vertices that become pivotal part of the collocation type. The selection of the other dependents to the WVC, are based on the nearness and the matching of the relationship with the vertices of the WVC. |
| The Maximum match algorithm is considered to find the set of vertices that depend on the WVC. |
 |
| The user specified threshold fixes the min-dominance and max-dominance. The more weighted features among the features are the features that contain count and weight more than the user specified threshold. The resultant collocation pattern is represented appropriately as principal-ranking structure weighted vertex graph, which reflects all the dimensions of the spatial knowledge. Following the greedy heuristic of sampling the vertices of a Weighted-Vertex Graph (WVG): |
| The Set-Cover (SC) and the Weighted-Vertex-Cover (WVC) are derived from the WVG. The candidate Weighted- Vertex Cover (i.e., wvc1) that is principal for the structure, represents the dominant features of the spatial domain, and the Set-Cover (i.e., sc1) represents a set of vertices that are ranked based on the dependencies on the principal. |
| The programming approach to represent the above graph in a data structure is an object-oriented paradigm. Where all the WVCs (component of principal in the principal-ranking structure) are represented as the parent classes and conceptually identified as principal in this work, all the SCs are represented as the children surrounding the parent, a categorical subtree under the principal tree. |
| A principal-ranking structure given in the Figure 4.2 is designed for representing a collocation pattern, which is a conceptually suitable structure to represent the collection of collocations. Features of high-dominance are stored in the principal and the other features are categorized into various subtrees under the principal. Thus the principal-ranking structure is useful for representing the various aspects of the spatial knowledge according to their dominance factors. |
EXPERIMENTAL WORK
|
| The experimental work is carried out with the principles of mathematical approximation of data. The approach has made an attempt to study the concept of collocation and its salient parts distinctly and describe the relevant structure to store spatial knowledge. Schematic and mathematical assumptions are made throughout the experiment to bring forward the better structure that can help GIS, store and retrieve the knowledge. Consider S1 to Sn are the spatial objects shown in the geographical map, where each spatial object inherently possesses some features. Let us interpret approximations for the experiment as follows: |
| Each spatial object has features, which are defined by several fuzzy sets [11]. The holder of each fuzzy set that defines the feature is represented by feature type. That means, a feature holds a feature type and a fuzzy set called as feature set which denotes several values for expressing the intensity of the feature in the spatial object. Where a = b = c = d = e may also apply for the approximations. According to [3][4][12][13] and others, the spatial features are designated as Boolean spatial features, which practically can represent only the presence or the absence of the features. |
Values of the feature pertaining to a spatial object are more important and care should be taken that the object and the features could not be ignored at any instance of mining activities. The reason why the values which belong to the feature are set of values of a fuzzy set is to describe the intensity of the features with several gradients. Let Z indicate a candidate fuzzy set. f1 of S1 is defined by 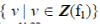 similarly f2 of S1 is defined by similarly f2 of S1 is defined by 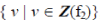 where the size (elements of fuzzy set) of feature arbitrarily differs. where the size (elements of fuzzy set) of feature arbitrarily differs. |
| The entire process of experiment is vested completely on non-spatial feature of spatial objects with fuzzy set values: |
| Hospital contains; crowd, working-hours and medication. |
| crowd is a feature which can be expressed in values as {dense, moderate, scant, mean, low, nil}. |
| working-hours is feature which can be expressed in values as {overtime, fulltime, part-time, visiting-time, lean-time, nil}. |
| medication is feature which can be expressed in values as {available, sufficiently-available, scantily-available, notavailable/ nil}. |
| Fuel-station also contains; crowd, working-hours along with storage-capacity: |
| storage-capacity defines the amount of service that the petrol-bunk can offer to the customers, the values that describe this feature are {available, sufficiently-available, scantily-available, not-available/nil}. |
| The working-hours depends on the storage-capacity of the petrol bunk. |
| School also contains working-hours, scholastic-offers and medication. |
| scholastic-offers describe the features pertaining to the education of the student in the school. medication, however a weak feature that seem to be irrelevant, but functionally the school may organize a medicating facilities which provides medication to the students. This feature may carry the same values that are used by the object which treats this feature as mandatory. |
Support Count and its Correction:
|
| Support Count is a statistic measure to find the dominance of the feature. Since storage-capacity – uses same fuzzy set as of the medication feature, adjustment can be made either to consider storage-capacity (3 times) or medication (3-times). In this example since storage-capacity behaviourally confines only to one object, which cannot be generalized, so only medication-3 is considered. |
Spatial Object – Features
|
Support Count Finalized:
|
| The overall count of the features used in the spatial domain for the spatial objects lists as Crowd-2, Workinghours- 3, Medication-3 which form the structural parts of the collocation pattern. |
Spatial Features and Spatial Objects:
|
| Spatial data sets are the key area for all the spatial data mining algorithms. Selection of the spatial data consisting of features for the spatial data mining is crucial when it comes for implementation. The spatial data is the representation of the spatial objects and their features that belong to a spatial layer [14]. The graph of spatial domain contains fundamental x and y co-ordinates and the description about the spatial objects and their features. This provides the ease of generating the collocation and contigs as similar to instance lookup scheme [15][16]. For imposing the fuzziness in the value of the features the randomization is implemented. A Java Based Random Semantic Map Data Generator, a tool developed to generate the spatial objects and their fuzzy representation of features. Randomization gives the clear scope of generating the features with more distinct alternatives for the spatial objects. sx and sy are the co-ordinates for the spatial objects with their name and type described as shown in Figure 4.4. Consolidated sets of the features are the other attributes of each object, where the attributes possess the gradient values, which are fuzzy in nature. Table.1 shows the sample data for the experiment. |
CONCLUSION
|
| The data structure described in this chapter is that fits all the requisites to store the spatial knowledge or collocation rule. Towards the application and integration of GIS, the feasible implementation of collocation rule that forms as a basic element of knowledge base of GIS is a more important concern; the structure has exceptional importance for the application relevant tasks. Particularly the idea of intensification of the meaning “the feature with fuzzy sets” and its representation has drawn more relevance. The representation of the structure is complex, and its various subscribed parts which have achieved not yet been applied by theorists is given with a proof of complexity and its performance evaluation. A join less approach of finding the collocations is worked out as a background of the experiment. The type discussed in this work ideally suits to store the nuggets of spatial. |
ACKNOWLEDGMENT
|
| Sincere thanks to management, Principal and faculty members of our institute (Sagi Ramakrishnam Raju Engineering College). |
| |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
| |
References
|
- Paul Hoogendijk, “What is datatype?” ,Project at Fujitsu, University of Japan, 1993-94.
- M. Nagabhushana Rao [M.N.Rao], P.Govindarajulu, “Spatial Disaster Identification, A Spatial Data Mining Approach”, International Conference on Systemic, Cybernetics and Informatics, Jan-4-6, Vol. 1 of 2, pp. 610-616, 2006.
- RongrongJi, Hongxun Yao, Qi Tian, Pengfei Xu, Xiaoshuai Sun XianmingLiu,“Context-Aware Semi-Local Feature Detector”, ACM Transactions on Intelligent Systems and Technology(TIST) archive ,Volume 3 Issue 3, May 2012 , Article No. 44
- Huang Yan, ShashiShekhar, Hui Xiong, “Discovering Collocation Patterns from Spatial Data Sets: A General Approach”. IEEE Transactions on Knowledge and Data Engineering, Vol. 16, No. 12, Dec 2004.
- Hans-Peter Kriegel, Peer Kroger, Jorg Sander, Arthur Zimek 2011."Density-based Clustering".WIREs Data Mining and Knowledge Discovery 1 (3): pp 231–240.
- Richard Schmied, Claus Viehmann ,“Approximating Edge Dominating Set in Dense Graphs”, 8th Annual Conference, TAMC 2011, Tokyo, Japan, May 23-25, 2011, Volume 6648, pp 37-47
- Reuven Bar-Yehuda, Danny Hermelin, DrorRawitz, “Minimum Vertex Cover in Rectangle Graphs”, 18th Annual European Symposium, Liverpool, UK, September 6-8, 2010
- Zhi-Zhong Chen, G. Lin, and L. Wang. An Approximation Algorithm for the Minimum Co-Path Set Problem. Algorithmica, Vol. 60, pp. 969-986, 2011.Rajeev Motwani, Lecture notes on “Approximation Algorithms”: Volume 3, Publisher: Stanford University, Stanford, USA, 2012.
- Falk Hüffner, Christian Komusiewicz, Hannes Moser, Rolf Niedermeier, “Fixed-Parameter Algorithms for Cluster Vertex Deletion”, Theory of Computing Systems, Volume 47, Issue 1 , pp 196-217, 2010.
- M. Nagabhushana Rao, P.Govindarajulu, “Collocation Pattern Analysis: A Variable Size/Shape Analysis”, International Journal of ComputerScience and Network Security, Vol.6. No-10, pp. 21-28, Oct – 2006.
- G.Manikandan | Dr. S.Srinivasan, “Mining Of Spatial Co-Location Pattern Implementation ByFp Growth”, Indian Journal of Computer Science and Engineering ISSN 0976-5166, Volume: 3; Issue: 2; Start page: 344; Date: 2012;
- M. Venkatesan, ArunkumarThangavelu, P. Prabhavathy, “A New Data Mining Approach to Find Co-location Pattern from Spatial Data”, First International Conference, ACITY 2011, Chennai, India, July 15-17, 2011.
- ShashiShekhar, Pusheng Zhang, Yan Huang, Ranga Raju Vatsavai, “Trends in Spatial Data Mining”, book chapter in Datamining : Next generation challenges and future directions , AAAI/MIT Press, 2003.
|