Department of Mathematics/Statistics, University of Port-Harcourt, P.M.B.5323, Port-Harcourt, Rivers State, Nigeria
Received: 28/11/2015 Accepted: 27/01/2016 Published: 31/01/2016
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
This work aims at modelling the Naira exchange rates for US Dollars Xt and Swiss Franc Yt using a transfer function (TF) technique. Data for the two currencies were obtained from the Central Bank of Nigeria (for a period of 53 years). After obtaining stationarity of the two series using appropriate transformation, the input series xt was pre-whitened to remove the spurious correlation effect. The output series yt was also pre-whitened and the cross correlation between the pre-whitened input (αt) and output (βt) was examined. From the behavior of the cross correlation, rational polynomial representation 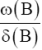 of the dynamic transfer function was obtained. The estimated noise
of the dynamic transfer function was obtained. The estimated noise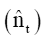 was found to be auto correlated. Thus, the noise was modelled separately using Box and Jenkins autoregressive (AR) method. This provided the missing component of the TF model which was used to fit the overall model. The resulted model underwent a diagnostic check and was found to be appropriate. Hence forecast was generated.
was found to be auto correlated. Thus, the noise was modelled separately using Box and Jenkins autoregressive (AR) method. This provided the missing component of the TF model which was used to fit the overall model. The resulted model underwent a diagnostic check and was found to be appropriate. Hence forecast was generated.
Transfer function, Pre-whitening, Cross correlation, Rational polynomial, Noise model, Stationarity.
Basically, no country is completely economically independent. Every country must depend on one or several countries for her economic growth. All nations are inter-dependent, because they have limited resources and have to trade with each other to satisfy their wants. This implies that the analysis of economic variables such as gross domestic product (GDP), inflation, exchange rates etc. are of paramount importance to any nation’s growth. Unfortunately in most African countries, less attention is paid to the study and monitoring of the rise and falls of these essential and sensitive variables. A volatile or inappropriate exchange rate has been a major hindrance to the growth of many African countries which Ghana is inclusive Appiah and Adetunde [1].
Exchange rates vary largely according to extent and nature of each country’s exposure to trade and global financial markets. In some stable economies, exchange rates of currencies compete favorably while the developing economies appear to be influenced heavily by the developed ones. This is because, the less developed countries receives less attention concerning exchange rate compared to the developed or industrialized economies [2].
The currencies of many sub-Saharan African countries faced depreciations with respect to US Dollar at the onset of the global financial crisis. According to Ltaifa, et al. [3], five countries: Ghana, Kenya, Nigeria, Uganda and Zambia depreciated by at least 20% between June 2008 and March 2009; while Tanzania and Rwanda depreciated by10% or less during same period.
According to Jeffrey [4], Argentina being the victim of the worst market financial crisis in 2001; experienced problems in the late 1990’s and the situation became severe because of its link with a particular currency, the US Dollar. The Dollar gained value over other major currencies beginning in the mid-1995, and caused the market for Argentina’s important agricultural export products (wheat, meat and soya beans) to decline sharply. Thus, the decline in the prices of these commodities expressed in Dollar was particularly dramatic. All these put together, led to sharp increase in the ratio of debt to exports.
Some earlier studies suggest that instability in exchange rate has the potential to affect a country’s economic performance. In Nigeria, the value of Naira has depreciated significantly compared with other currencies due to poor economic management, political system and other unknown factors. However, a close observation of the Naira exchange rate for US Dollar and Swiss Franc shows that the two currencies are highly related. Thus, studying the behavior and relationship of these two currencies in relation to Naira can provide useful information for the economy of the two Countries (USA and Switzer Land) and Nigeria at large. This work therefore, intends to build a model that establishes the relationship between the two currencies (US Dollar and Swiss Francc) in relation to Nigeria’s currency (Naira). The model is called the transfer function model.
Transfer function model (TFM) is a statistical model describing the relationship between an output variable and one or more input variables [5]. TFM can be a single equation or multiple equation model, which the latter could be referred to as a simultaneous transfer function (STF) model [6-8]. Some authors will prefer to distinguish the two models as single-input and multiple-input transfer function models. In most applications, linear equation is used to describe the relationship resulting from the distributed-lag model.
Elkhtem, et al. [9] considered the nature of crude oil as a mixture of hydrocarbons with different boiling temperatures. Control became essential for the fractionation column to keep products at the limitations. The paper revealed the identification of transfer function for relevant different developed control strategy and relevant transfer function were identified using MATLAB Software.
A Work on forecasting foreign exchange by Znaczko [10] investigated a transfer function model with multiple variables. The study revealed that the best forecast of foreign exchange rates depends on current and past prices.
Kannan and Farook [11] fitted a transfer function model to global warming entities such as atmospheric temperature, and atmospheric CO2 emissions. A strong relationship was demonstrated between annual atmospheric CO2 emissions and present/ past atmospheric temperature.
Practically, the output is not a deterministic function of the input. Transfer function model is quite different from the ARIMA model. The latter is a univariate time series model while the transfer function model is a multivariate time series model. The ARIMA model relates the series only to its past, but beyond this indication, the transfer function model will relate the series to other time series [12]. Due to the close relationship with the regression models, the transfer function models are also referred to as dynamic regression models [13]. The transfer function models can use more than one explanatory variable, but the explanatory variables must be linearly independent of each other [14].
Transfer function approach as a method of data analysis, has been in use for some decades. Virtually every field of study has demonstrated the importance and relevance of the transfer function approach especially in its ability to enhance forecast based on relating different series. In a stable economic trend, such model can enable a researcher or planner to predict favorable chances an indigenous economy stands amidst higher ones in the global market.
In time series analysis, the Box-Jenkins method describes the transfer function model as a model that predicts future values of a time series (output series) from past values of same series and one or more related series (input series).
In this work, however, we intend to apply the Box-Jenkins method and the pre-whitening approach to build a transfer function- AR noise model of Naira exchange rates for the US Dollar and Swiss Franc. In our method, the leading indicator is identified and the noise component is modeled separately and added to the dynamic relationship between the input and output series. The resulting noise is found to satisfy its basic assumptions [ εt ˜ NIID(0,á2) ] thus showing that the model is adequate.
Let Xt and Yt be two time series.
The time series Xt is said to be stationary if the statistical properties are essentially constant through time. In other words, 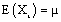 and
and 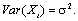 In this work, stationarity is obtain by differencing. That is,
In this work, stationarity is obtain by differencing. That is, 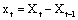 .
.
Pre-Whitening
Pre-whitening approach involves finding autoregressive integrated moving average (ARIMA) model for Xt that yields white noise residuals while the functional relationship between the Xt and Yt is still maintained.
For this work, an ARIMA (p,d,o) model is identified and we have
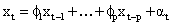
Rewriting the equation, the residuals or the pre-whitened input 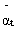 is obtained as
is obtained as
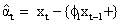
The Yt is substituted for Xt to get the filtered equation for the pre-whitened output as:
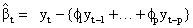
By pre-whitening, cross correlation accurately reflects the structure of the impulse function [15]. Here, α and β represent the pre-whitened input and output series respectively.
The cross correlation for lag k is given as
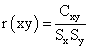
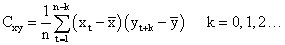
Where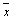 and
and 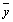 are the sample means of Xt and Yt, st and sy are the sample standard deviations respectively.
are the sample means of Xt and Yt, st and sy are the sample standard deviations respectively.
The dynamic relationship between input series Yt and output series Xt is usually approximated by a linear transfer function
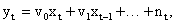
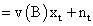
Where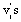 are the transfer function weights and is a noise term. Estimates of the transfer function weights can be calculated from
are the transfer function weights and is a noise term. Estimates of the transfer function weights can be calculated from
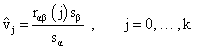
Where sα and sβ are the estimated standard deviations of the pre-whitened input and the output data respectively.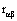 is the estimated cross correlation between the pre-whitened input and output. Insignificant weights are rounded off to zero. B denotes the backshift operator such that
is the estimated cross correlation between the pre-whitened input and output. Insignificant weights are rounded off to zero. B denotes the backshift operator such that 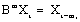
The function v (B) determines the impact of input Xt on Yt; and
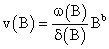
Thus, Yt can be represented as
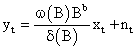
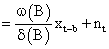
According to Box and Jenkins [16], the parameters in v (B) are estimated by the equation
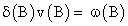
Explicitly, it can be expressed as,
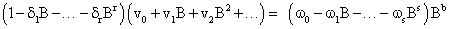
The parameters r, b, s, represent the order of the numerator polynomial , the delay parameter that indicates the time lag until input affects the output also called dead-time or delay time, and order of the denominator polynomial respectively .
In the model identification, v (B) parameters are obtained and fitted; and the noise term nt is added. In this concept, however, it is believed that the noise nt could be serially correlated; thus violating its assumption. The noise is then modeled separately using Box and Jenkins method as:
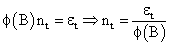
Where,
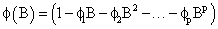
and p is the autoregressive order of nt and øi’s are the autoregressive parameters.
Thus the resulting model is:
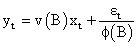 and εt is found to be serially uncorrelated as expected.
and εt is found to be serially uncorrelated as expected.
The analysis of the data available for this thesis was carried out using Minitab software. Data used was secondary data with fifty three observations each (1960-2013). We intend to build a transfer function -AR noise model which could be used for future forecast of the naira exchange rate for the two currencies. Let Xt denotes the Naira exchange rate of US Dollar and Yt, the Naira exchange rate of Swiss Franc
In the language of our study, Xt is the input series and Yt the output series.
Figure 1 (appendix) demonstrates the combined raw data plot for Xt and Yt.
From these plots, it is observed that the series are not stationary. This demanded for an appropriate transformation to make them stationary.
The correlation between Xt and Yt gives 0.996. This value indicates a strong positive relationship between the two series. This is also evident in Figure 1.
Xt and Yt were both differenced once to obtain stationarity.
An ARIMA (1,1,0) was identified for the Xt resulting in the model:
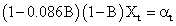
From the above model, the pre-whitened Xt is:
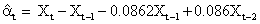
and that of Yt
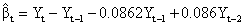
The cross correlation of the pre-whitened series rαβ are seen in Figure 2 below. Since the rαβ at lag and are not statistically significant, the weights v0 and v1 are systematically equal to zero. Thus from the figure; b=2, s=1 and r=2. In addition, since 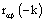 are not statistically different from zero; it means the present values of Yt are related to the past values of Xt and not otherwise. Hence, Xt is the leading indicator. The four transfer function significant weights are shown in Table 1 below with their respective cross correlations and lags.
are not statistically different from zero; it means the present values of Yt are related to the past values of Xt and not otherwise. Hence, Xt is the leading indicator. The four transfer function significant weights are shown in Table 1 below with their respective cross correlations and lags.
We had earlier expressed in methodology that:. 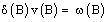
That is, 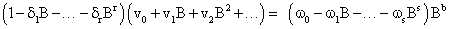
Substituting b=2, s=1 and r=2, we have
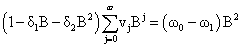
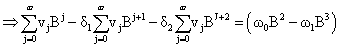
Solving the above equation, we have
δ1=0.7157, δ2=0.5750, ω0=0.5750; ω0= - 0.2741,
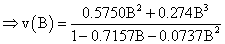
The noise 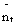 is estimated as
is estimated as
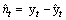
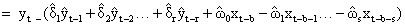
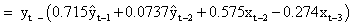
Autocorrelation and partial autocorrelation function for nt: The autocorrelation function decays exponentially to 0, while the partial autocorrelation function cut off after lag 1 (Figures 3 and 4). Thus the identified model is ARIMA (1,0,0) which is equivalent to AR(1) (Table 2).
Writing the model explicitly, we have
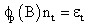
So that 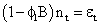
and 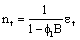
Combining the two models, we have
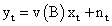
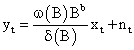
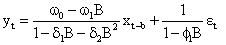
The final transfer function-AR noise model is obtained as;
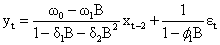
Where 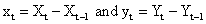
To check for model adequacy, the following diagnostic check was applied.
The autocorrelation function of the residual term εt (Figure 5) below demonstrates no particular pattern or spikes. No autocorrelation is significant. This indicates that the residual follows a white noise process. Hence the fitted model is adequate.
Having tested the adequacy of the transfer function AR noise model and was found to be appropriate; next is to generate forecasts. The forecasts of the next ten years are presented in Table 3.
This work provides a solution to a dynamic relationship where the residual fails to follow a white noise process or violate its usual assumptions. The work modeled the residual obtained from fitting the transfer function (TF) model separately. The ARIMA model obtained from the TF noise is added to the major component of the model resulting in transfer function autoregressivenoise model. Data from naira exchange rate of US Dollars and Swiss Franc (1970-2013) was used to demonstrate the workability of the model. The model was found to be appropriate and forecasts for the Naira exchange of Swiss Franc were generated using the model.