Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Analysis of Partitional Clustering Methods for Nonlinear Hybrid Dynamical Systems

Ankit K. Shah1, Dipak M. Adhyaru2
  1. Assistant Professor, Dept. of Instrumentation & Control, SardarVallabhbhai Patel Institute of Technology (SVIT), Vasad, Gujarat, India 1
  2. Section Head, Dept. of Instrumentation & Control, Nirma University, Ahmedabad, Gujarat, India2
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Nonlinear Hybrid Dynamical Systems (NHDS) are characterized by interacting dynamics of continuous and discrete domain. Application such systems has been reported in chemical systems, manufacturing systems, mechanical systems, electrical systems, telecommunication systems, automobile control and computer disk drive control.The nonlinear continuous dynamic in NHDS will change due to occurrence of some unknown discrete events. So, for identification of NHDS, it is required to classify the open loop data according to discrete events. Clustering is the process of organizing objects into groups whose members are similar in some way. A variety of algorithms have recently emerged that meet these requirements and were successfully applied to real life data mining problem. Fuzzy cmeans (FCM) and k-means are commonly used partitional algorithm based on unsupervised learning methods. This paper focuses on the analysis of FCM and k-means partitional clustering methods for the single tank NHDS data classification.

Keywords
Nonlinear Hybrid Dynamical Systems; Clustering; Fuzzy c-means; k-means.

INTRODUCTION
Classical control theory makes use of models of dynamic systems, whose state evolution is described by smooth linear or nonlinear differential equations. However, many dynamical systems around us also depend on occurrences of discrete events along with the evolution of continuous dynamical states [1]. Systems which are characterized by interacting continuous-time nonlinear dynamics and discrete event dynamics are called the Nonlinear Hybrid Dynamical Systems (NHDS). When continuous and discrete elements work together in a process and there is a considerable relation between these elements, it is necessary to model dynamical elements. That is why in recently many researchers have concentrated their efforts on modeling and control of hybrid systems [2, 3].
Application of such hybrid dynamical systems have been reported in chemical systems, manufacturing systems, mechanical systems [4], telecommunication systems, automobile control and computer disk drive control among others. Thus, hybrid dynamical systems arise in a large number of application areas but the control of such hybrid dynamical systems is often based on heuristics resulting from plant operation. Several strategies that model the hybrid system by formally integrating the continuous and discrete variables have been presented in the literature [1-3]. For model identification of such combine dynamical systems, it is required classify the data according to discrete events. In [5-10], different clustering based data classification algorithms are used for hybrid dynamical systems. Clustering is the process of organizing data into groups whose members are similar in some way [11]. Clustered data can be in form of images, shopping items, patterns, observations, feature vectors, words, documents, shopping items etc. The goal is to divide the data-set in such a way that objects belonging to the same cluster are as similar as possible, whereas objects belonging to different clusters are as dissimilar as possible. Clustering constitutes an essential component of data mining, a process of exploring and analysing large amounts of data in order to get useful information.Clustering is the unsupervised classification of patterns into groups [12]. In an unsupervised classification problem, no predefined classes are given but data objects or individuals should form a number of groups so that distances between a pair of objects within a group should be relatively small and those between different groups should be relatively large. Only some mathematical criteria can decide on the composition of clusters when classifying data-sets automatically. Therefore clustering methods are endowed with distance functions that measure the dissimilarity of presented example cases, which is equivalent to measuring their similarity. As a result one yields a partition of the data-set into clusters regarding the chosen dissimilarity relation. Clustering approach can used for the data mining, text mining, information retrieval, web analysis, marketing, medical diagnostics, computational biology and many other applications. A variety of algorithms have recently emerged that meet these requirements and were successfully applied to real-life data mining problem [13]. In general clustering algorithms can be classified in to two categories: Hierarchical algorithms and Partitional algorithms.Hierarchical clustering algorithms produce a nested series of partitions based on a criterion for merging or splitting clusters based on similarity. Partitional clustering algorithms identify the partition that optimizes (usually locally) a clustering criterion [11]. Partitional methods have advantages in applications involving large data sets for which the construction of a dendrogram is computationally prohibitive. A problem accompanying the use of a partitional algorithm is the choice of the number of desired output clusters must be specified. The partitional techniques usually produce clusters by optimizing a criterion function defined either locally or globally. Partitional clustering algorithm mainly classified in to two kinds: k-means and fuzzy c-means algorithms.
The k-means clustering method is crisp partitioning, in which every given object is strictly classified into a certain group [14, 15]. The k-means clustering method is efficient for processing large data sets. The boundaries defined for the objects are very sharp and so is classified in one and only one cluster. The various modified k-means clustering based algorithms also proposed in [16, 17]. Fuzzy logic is logic of fuzzy sets; a Fuzzy set has, potentially, an infinite range of truth values between one and zero. Propositions in fuzzy logic have a degree of truth and membership in fuzzy sets can be fully inclusive, fully exclusive, or some degree in between. The fuzzy set is distinct from a crisp set that it allows the elements to have a degree of membership [18]. The core of a fuzzy set is its membership function. It is a function which defines the relationship between a value in the sets domain and its degree of membership in the fuzzy set. Fuzzy C-Means (FCM) algorithm of clustering allows one piece of data to belong to two or more clusters. This method developed by [19] and further improved by [20, 21], is frequently used in pattern recognition [20, 22].
The NHDS data set containing of both numeric and categorical values along with continuous dynamic, so we are interested in algorithm which efficiently provide partition of the data set of hybrid system. The aim of this paper is to analyse efficiency of the k-means and FCM partitional clustering algorithms for classification of hybrid dynamical system data according to discrete events. The structure of the paper is as follows. The k-means hard clustering algorithm for data classification of unsupervised data is presented in Section 2. The Fuzzy C-Means clustering algorithm for classification of unsupervised data is presented in Section 3. In Section 4, example of data classification of random data set using k-means and fuzzy c-means algorithms. Section 5 offers application of k-means and fuzzy cmeans algorithm for classification of single tank NHDS. Finally, Section 6 summarizes the analysis of partitional clustering methods for hybrid system data classification and gives the future scope of this analysis.

K-MEANS CLUSTERING ALGORITHM
The k-means clustering algorithm referred as hard partitioning algorithm which approximates the maximum likelihood solution for determining the location of the means of a mixture density of component densities.Objects to be clustered are denoted by k, where k is the number of clusters. The abbreviated symbol C = (c1,…, ck) is used for complete collection of cluster centers. Given a set of n-observations in p-dimensional Euclidean space, k-means clustering aims to partition the n-observations to in k sets (k < n) so as to minimize the within-Cluster Sum of Squares (WCSS). The objective function of the k-means clustering can be defined as [16, 17]:
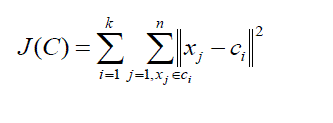image(1)
where, ci is the mean of points in the ith cluster.The first step to select k points as the initial value of cluster centers (means) as ( ,..., ) 1 1 c c and the termination criteria . Than assign all data points to their closest cluster center ci based upon the Euclidean distance between each point and each cluster center denoted by:
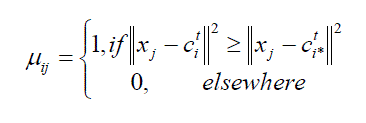image(2)
For all i, k. Now, each cluster center mean is recomputed as the average of the points in that cluster by:
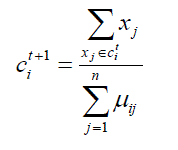image(3)
Repeats (2) and (3) until t the mean of cluster centers do not change
The main advantages of this algorithm is its simplicity and speed which allows it to run on large data sets. Its disadvantage is that it does not yield the same result with each run, since the resulting clusters depend on the initial random assignments and thus represent a local minimum. It minimizes intra-cluster variance, but does not ensure that the result has a global minimum of variance. Another disadvantage is their performance may be compromised by the presence of outliers. The discreteness of each cluster makes the k-means analytically and algorithmically intractable. The biggest drawback of a hard partitioning is the concept that it either includes a data point in a partition or strictly excludes it; there is no other chance for the data elements to be part of more than one partition at the same time. However, in natural clusters it is always the case that some of the data elements partially belong to one set and partially to one or more other sets. In order to overcome this limitation, the notion of fuzzy partitioning was introduced which is discuss in next section.

FUZZY C-MEANS (FCM) CLUSTERING ALGORITHM
Fuzzy logic is logic of fuzzy sets; a Fuzzy set has, potentially, an infinite range of truth values between one and zero. Propositions in fuzzy logic have a degree of truth and membership in fuzzy sets can be fully inclusive, fully exclusive, or some degree in between [18]. The fuzzy set is distinct from a crisp set that it allows the elements to have a degree of membership. The core of a fuzzy set is its membership function. It is a function which defines the relationship between a value in the sets domain and its degree of membership in the fuzzy set.Fuzzy C-Means (FCM) algorithm of clustering allows one piece of data to belong to two or more clusters. Objects to be clustered are denoted by where k is the number of clusters. Abbreviated symbol C = c1, …, ck is used for complete collection of cluster centers. Given a set of n-observations inp-dimensional Euclidean space, FCM clustering aims to partition the nobservation in to k sets (k<n) so as to minimize the within-cluster Sum of Squares (WCSS). The FCM minimizes the following objective function [19, 20]:
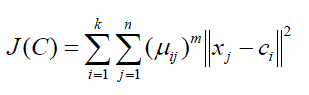image(4)
where, n is the number of data items, k is the number of clusters with 2 k < n, xj is j-th measure data of p-dimension, ;ij is the degree of membership of xj in the ith cluster, m& is a weighting exponent which determines the degree of fuzziness of the resulting clusters, . is any norm expressing the similarity between any measured data and the center. For m = 2, this is equivalent to normalizing the membership linearly to make their sum 1. When value of m is close to 1, then cluster center closest to the point is given much more weight than the others and the algorithm is similar to k-means. The membership matrix U = [ ij ] and its elements must fulfill the following constraints:
First step of FCM algorithm is to select value of k, m and termination criteria . Next step to select k points as the initial value of cluster centers (means) as ( ). Now, find the membership matrix U by minimized the objective function given in (4) and obtained solution is
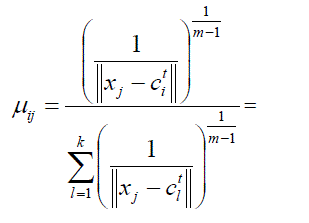image
Now find the vector of cluster center C by minimizing (4) and obtained solution is:
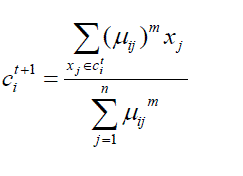`image
Repeat (5) and (6) until it satisfy the termination criteria tThe data points at the center of the cluster have maximum membership values and the membership gradually decreases when data points move away from the cluster center. Like the k-means, this algorithm also minimizes intra-cluster variance, but has the same problems as k-means, the minimum is a local minimum and the results depend on the initial choice of the cluster centers. It has better convergence properties as compare to k-means algorithm. The FCM needs to store U and all ci's and the alternating estimation of U and ci's causes a computational and storage burden for largescale data sets [23].

CLASSIFICATION OF RANDOM DATA SET
For the first analysis of above mentioned partitional clustering algorithms consider the example given in [24]. Four normally distributed random data sets with centers are (0.125, 0.25), (0.625, 0.25), (0.375, 0.75) and (0.875, 0.75), respectively, are generated for each of 200 samples. Now, above data sets are mixed together and generate the complete data set xj = [XjYj] of 800 samples shown in Fig. 1. The data set xj was clustered using k-means and FCM clustering algorithms with the assumption of four cluster centers.
Fig. 2(a) and Fig. 2(b) shows the results which were obtained using k-means and FCM algorithm, respectively. The cluster centers are shown as ,, * and O symbols. The FCM algorithm was used with fuzzy parameter m = 2 and termination criteria = 0.00001. Both the described clustering algorithms have been applied using Matlab software on the random data and the location of each cluster center derived. The final location of cluster center for each cluster using both the clustering algorithm shown in Table 1.

CLASSIFICATION OF SINGLE TANK NHDS
For identification of the NHDS it is required to classify the open loop data points according to their discrete events. Prior for identification of NHDS, data classification using clustering required selecting proper method for cluster given data. Both the partitional clustering algorithms are applied on single tank NHDS given in [9, 25] and obtained result was analyzed. A schematic diagram of the single tank NHDS was shown in Fig. 3. Given system has a hybrid characteristic due to it involves discrete event as water level inside the tank changed its height beyond 0.3 cm.
Mass balance and Bernouilli law for the single tank nonlinear hybrid system given by (7) and (8):
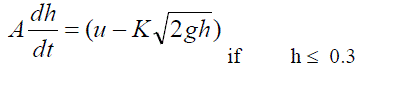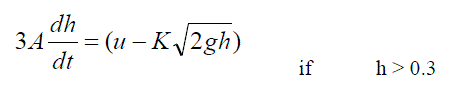image
image
where, A=0.0154 m2 is the cross section of the tank and K = 2 10-4 m2 is the cross section of the outlet hole, u is the input flow rate, g = 9.81 m/sec2 is the gravity constant and h is the level of the tank.The given hybrid single tank system is divided into two regions because the cross section of the tank changes when the level is higher than 0.3. A set of data set xj = [hj uj-1] are generated for the 1000 samples with sampling time 1 sec and by using a random input uj with values between 0 and 0.001. A random bounded 3% error has been added to the measured level hj. The open loop simulated hybrid single tank response of input and output shown in Fig. 4. The FCM and k-means algorithms have been applied to data set xj with the assumption that the system has two cluster centers. Cluster centers are shown as and O symbols. The fuzzy clustering algorithm used with fuzzy parameter m = 2 and termination criteria =0.00001. The kmeans algorithm has been used with a termination criteria =0.00001.Fig. 5(a) and Fig. 5(b), shows the partition results of the k-means and FCM clustering algorithm using the open loop data set of hybrid single tank system. In Table 2, the classification results for h 0.3 and h > 0.3 given with the actual number of data point and number of data points partitioned using FCM and k-means algorithms.

CONCLUSION
In this section analysis of the k-means and FCM partitional algorithms is carried out based on above two examples. Table 1 show that the average estimation error to locate the cluster centers using FCM is less as compare to k-means. Table 2 gives the information that the classification and misclassification error of given hybrid system data points for type 1 and type 2 regions. The k-means clustering method is easy to implement. The biggest drawback of the k-means clustering is the concept that it either includes a data point in a partition or strictly excludes it; there is no possibility for the data to be part of more than one partition at the same time. However, in natural clusters it is always the case that some of the data elements partially belong to one set and partially to one or more other sets. The FCM allow the data point to a part of more than one set using membership function. Aside from assigning a data point to clusters in shares, membership degrees can also express how ambiguously or definitely a data point should belong to a cluster. Compared with the k-means it is quite insensitive to cluster centers initialization and it is not likely to get stuck in an undesired local minimum of its objective function in practice. Given analysis useful forthe classification of open loop data for the NHDS, which is useful for identification and control of hybrid systems.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
 

References
  1. A. van der Schaft, H. Schumacher, “An Introduction to Hybrid Dynamical Systems”, Springer-Verlag, London, 2000.

  2. V.S. Branicky, S.K.M. Borkar, “A unified framework for hybrid control:model and optimal control theory”, IEEE Trans. Automatic Control, Vol.43, pp. 461-474, 1998.

  3. A. Bemporad, M.Morari, “Control of systems integrating logic. dynamics and constraints”, Automatica, Vol. 35, pp. 407-427, 1999.

  4. M. Hirata, Y. Hashimoto, S. Noguchi, S. Adachi, “A hybrid modeling method for mechanical systems. Mechatronics”, Vol. 20, pp. 59-66, 2010.

  5. G. Ferrari-Trecate, M. Muselli, D. Liberati, M. Morari, “A clustering techniques for the identification of piecewise affine systems”, Automatica, Vol. 39, pp. 205-217, 2003

  6. A. Bemporad, A. Garulli, S. Paoletti, A. Vicino, “A bounded-error approach to piecewise affine system identification”, IEEE Transactions on Automatic Control, Vol. 50, pp. 1567-1580, 2005.

  7. H. Nakada, Takaba K.,T. Katayama, “Identification of Piecewise affine systems based on statistical clustering technique”, Automatica, Vol. 41, pp. 905-913, 2005.

  8. M. Tabatabaei-Pour, M. Gholami, K. Salahshoor, H. R. Shaker, “Recursive identification of piecewise affine hybrid systems", IEEE proceeding of 9th International conference on Control, Automation, Robotics and Vision, pp. 1-6, 2006.

  9. M.E. Gegundes, J. Aroba and J.M. Bravo, “Identification of piecewise affine systems by means of fuzzy clustering and competitive learning”, Eng. Appli. Artificial Intelli., Vol. 21, pp. 1321-1329, 2008.

  10. S. Ghosh, S. Maka, “A fuzzy clustering based technique for piecewise affine approximation of a class of nonlinear systems”, Commun Nonlinear Sci Number Simulate, Vol. 15, pp. 2235-2244, 2010.

  11. A.K. Jain, M.N. Murty, P.J. Flynn, “Data clustering: A review”, ACM Comput. surveys, Vol. 31, pp. 264-323, 1999.

  12. R. Xu and D. Wunsch,“Survey of clustering algorithms”, IEEE Trans. Neural Networks, Vol. 16 ( 3), pp. 645-678, 2005.

  13. Berkhin, “Survey of clustering data mining techniques”, Technical report, Accrue soft-ware, CA, 2002.

  14. S.Z. Selim, M.A. Ismail, “K-means type algorithms: a generalized convergence theorem and characterization of local optimality”, IEEE Trans.Pattern Anal. Mach. Inteli, Vol. 6 , pp. 81–87, 1984.

  15. T. Kanungo, D. M. Mount, N. S. Netanyahu, C. D. Piatko, R. Silverman, and A. Y. Wu, “An efficient K-means clustering algorithm: Analysisand implementation”, IEEE Trans. Pattern Analysis and Machine Intelligence, Vol. 24(7), pp. 881-892, 2000

  16. G. Patane and M. Russo, “Fully automatic clustering system”, IEEE Trans. Neural Networks, Vol. 13(6) ,pp. 1285-1298, 2002.

  17. M. C. Su and C. H. Chou, “A modified version of the K-means algorithm with a distance based on clustersymmetry”, IEEE Trans. Pattern Analysis and Machine Intelligence, Vol. 23(6), pp. 674-680, 2001

  18. J. S. R. Jang, C.-T. Sun, and E. Mizutani, “Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence”, Prentice Hall, 1996.

  19. J. C. Bezdek, “Cluster validity with fuzzy sets”, Journal of cybernetis, Vol. 3(3), pp. 58-73, 1973.

  20. J. C. Dunn, “Some recent invesingations of a new fuzzy partitioning algorithm and its application to pattern calssification problems”, Journal of cybernetics, Vol. 4(2), pp. 1-15, 1974.

  21. J. C. Bezdek, N. R. Pal, “Some new indessess for cluster validity, IEEE transcation on systems man and cybernetics”, Vol. 28(3), pp. 301-315,1998.

  22. I. Gath, A.B.Geva, “Unsupervised optimal fuzzy clustering”, IEEE Trans. Patt. Anal. Mach. Int., Vol. 2, pp. 773-781, 1989.

  23. K.-L. Du, “Clustering: A neural network approach”, Neural Networks, Vol. 23, pp. 89-107, 2010.

  24. Xiong, K.C., “Towards an unsupervised optimal fuzzy clustering algorithm for image database organization”, IEEE Comput. Society, Vol. 3, pp. 3909-3912, 2000.

  25. A. K. Shah, D. M. Adhyaru, “Fuzzy based selection of PWARX model for the nonlinear hybrid dynamical systems”, IEEE proceeding of 3rd International Conference on NUiCONE, pp. 1-6, 2013.