Investigating the Choline Chloride: Urea and Choline Chloride: Glycerol Deep Eutectic Solvents as Nanofluids Dispersants for Convective Heat Transfer

Abstract

In this paper, two Deep Eutectic Solvents (DESs), choline chloride: urea and choline chloride: glycerol with molar ratios of 1:2, respectively, were investigated as dispersants for Al2O3 nanoparticles (NPs) to study the heat exchange. Because of the DESs’ high thermal properties, especially at high temperatures, they became good candidates for heat transfer applications. We prepared the DESs and examined their thermal conductivity as a new approach data using a thermal conductivity meter. Nanoparticles loading ratios of 1, 2, 3, 4, and 5 vol.% was proposed to inspect the thermal effect. Viscosity, friction factor (f), Nusselt number (Nu), Prandtl number (Pr), Reynolds number (Re), and heat transfer coefficient (h) relationships were studied in details under laminar flow conditions. Results showed that both of the pristine DESs had higher heat transfer coefficients than the nanofluids at all loadings, which attributed to the high heat capacity of the DESs than the NPs materials. Here, the heat transfer coefficient of the nanofluids decreased by increasing the NPs loading. 

Keywords

Deep eutectic solvents, Nanofluid, Friction factor, Thermal conductivity, Nusselt number, heat transfer coefficient

Introduction

Nanofluids are the products of dispersing nanoparticles ( ≤ 100 nm) in fluids to upgrade their heat transfer properties [1]. This type of fluids was gaining attention since it was introduced, more than 20 years ago [2], due to the easiness in preparation and remarkable improvement in thermal properties [3]. Nanofluids were employed in a wide range of applications, including transformer oil [4], electronics industry [5-7], refrigerators and chillers [8,9], diesel combustion and electrical generators [10,11], pipes and heat exchangers [12,13], solar energy, nuclear reactors, space, cooling of machines, catalyst, and mass transfer [3].

Nanofluids are based on Brownian motion phenomenon, in which the particles are suspended in a fluid medium and the gravity has no effect due to their small size [1]. Different nanoparticles (NPs) such as, silica [14], aluminum oxide [15], and copper [16] were added to water [14], ethylene glycol [17], glycol [18], etc. to synthesize nanofluids mixtures. Many researchers assumed the nanofluids as a single-phase liquid, which neglected many physical impacts and calculations. Therefore, challenges to describe the suspension results conflicting, and poor mechanism understanding was reported [19].

“Deep eutectic solvents” is a term appeared in 2003 [20] to describe solvents formed by the hydrogen bond interaction between two, or more [21], materials containing a hydrogen bond donor (HBD) and hydrogen bond acceptor (HBA) [22]; the final product possesses a lower melting point than its raw materials. The DESs often have melting points lower than 100°C, including a group of liquids at room temperature [23,24]. For example, the DES produced by mixing choline chloride (mp=302°C) and urea (mp=133°C) 1:2 molar ratio, respectively, has a melting point of 12°C [20]. The DESs have many advantages, including, but not limited to, low flammability, low vapor pressure, inexpensive raw materials, environmentally green, broad electrical and thermal windows, biodegradable, safe, and easy to synthesize [25,26]. These exceptional properties made them good candidates for many applications [22].

Different DESs were reported as dispersants for nanoparticles which were used for different purposes. Martis et al. [27]reported the use of choline chloride: urea DES to disperse pristine and oxidized multiwall carbon nanotubes, p-MWCNTs and o- MWCNTs, respectively. It was found that p-MWCNTs had low dispersion in the DES, while o-MWCNTs well dispersed. Abbott et al. [28] successfully dispersed SiC and Al₂O₃ nanoparticles in choline chloride: ethylene glycol DES, which used for silver electrodeposition. Mota-Morales et al. [29] injected MWCNTs in choline chloride: acrylic acid DES, which was prepared in different molar ratios, to manufacture macroporous poly (acrylic acid)-CNxMWCNT complexes. Recently, Fang et al. [30] have investigated the dispersion of graphene oxide nanoparticles in several DESs, which were introduced as nanofluids. Promising results were observed regarding dispersion, stability, and thermal conductivity. Nevertheless, the use of deep eutectic solvents as nanofluids media is still not common; in fact, much work is needed to utilize this kind of solvents [31].

Choline chloride: urea and choline chloride: glycerol deep eutectic solvents were intensively investigated since their raw materials are safe and common [20,32,33]. These DESs have a wide thermal range [32], which promoted them for heat transfer applications. In this paper, the thermal conductivity of choline chloride: glycerol and choline chloride: urea DESs were measured and used to study the DESs as nanofluids dispersants for Al₂O₃ nanoparticles to examine the heat transfer. Friction factor, Nusselt number, Reynolds number, and heat transfer coefficient values were reported in the laminar flow region, due to DESs’ high viscosity (Table 1). The suggestion of using DESs for this type of application was due to their negligible vapor pressure, which made their usages safe, reliable, and overcame the water operation problems.

Table 1 : Greek symbols used during the study.

Materials

Choline chloride (ChCl, 99%, ACROS Organics), glycerol ( ≥ 99.5), and urea (99.0%) were purchased from Fisher Scientific (Pittsburgh, PA, USA) to prepare the DESs. A Millipore DI water system (18.2 MΩ.cm) produced by Synergy 185, EMD Millipore Corp. (Billerica, MA, USA) was used to provide water for cleaning purposes.

DESs Perpetration And Characterization

The DESs were prepared in accordance with a previously reported work [32]. The chemicals were used as received without further treatments. Both choline chloride: urea (DES1) and choline chloride: glycerol (DES2) mixtures were synthesized in ratios of 1:2, respectively. The mixtures were prepared by mixing the reactants and heating them to 80°C with stirring for several hours. Ultimately, colorless products formed, which were stored in sealed containers to prevent any possible moisture.

The thermal conductivity test was conducted using a TLS-100 thermal conductivity meter (ThermTest Inc, Fredericton, NB, Canada). The results were obtained at room temperature and repeated three times to calculate the average; the standard deviation was calculated and reported as error bars.

System Set up

The suggested system to use in this work was designed as shown in Figure 1 and used to investigate the heat transfer from a hot fluid to the nanofluid. The process consisted of two loops, each has a tank, pump, flow meter, and two thermocouples; both loops are connected to a shell and tube heat exchanger. The suggested length of the heat exchanger was 1 m, involved 40 tubes of 5 mm diameter. Different flow rates, from 100 to 300 L/min, and NPs loading, from 1% to 5 %, were used for calculations. Viscosity and density values used in this study calculations were based on our previous report [32,33], while the heat capacity was employed as stated in a previous work [34]. The mentioned properties were calculated for the nanofluids as well illustrated in the next section.

Figure 1: The suggested system diagram.

Data Processing

2-4-1 Density

The nanofluid density correlation was proposed by Pak and Cho [35], which can be defined as:

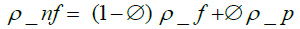(1)

where ρnf is the nanofluid density, ∅ the volume concentration of Al₂O₃ particles, ρf and ρp the base fluid and nanoparticles densities, respectively.

2-4-2 Specific heat capacity

Xuan and Roetzel [36] suggested a relation to calculate the nanofluid specific heat capacity as follows:

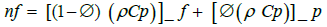(2)

where Cpnf, Cpf, and Cpp are the nanofluid, base fluid, and nanoparticles heat capacities, respectively.

2-4-3 Thermal conductivity

The nanofluid thermal conductivity was calculated using the equation introduced by Yu and Choi [37] as:

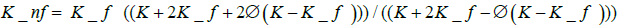(3)

where Knf, Kf, and K are the nanofluid, base fluid, and nanoparticles thermal conductivities, respectively.

2-4-4 Viscosity

Nanofluids viscosity was calculated using Einstein′s equation as suggested by Drew and Passman [38], which is applicable for spherical particles with fraction volume less than 5 vol%, as shown below:

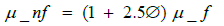(4)

where μnf and μf are the nanofluid and base fluid (DES) viscosities, respectively.

2-4-5 Friction factor

The friction factor for the pure DESs and nanofluids was estimated [39] as:

f = 64 / Re (5)

Reynolds number [40] can be calculated as below:

Re =VD /υ (6)

where V is the fluid velocity, D the tube diameter, and υ the Kinematic viscosity, which can be calculated by the following equation:

υ = μ / ρ (7)

2-4-6 Nusselt number

The base DESs and nanofluids Nusselt number was calculated by Seider-Tate equation [41] as presented below:

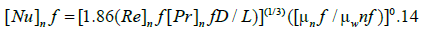(8)

where Nu is Nusselt number, Re Reynolds number, and Pr Prandtl number, which was calculated as [42]:

Pr = ([Cp]_ nf μ _ nf ) / K _ nf (9)

It is worth noting that μnf and μwnf were assumed equal in this study, which neglects the second term of the above equation.

The heat transfer coefficient for forced convection in laminar flow range [43] can be calculated by:

Nu _ nf = hD / K _ nf

where h, D, and K are heat transfer coefficient, tube diameter, and thermal conductivity, respectively.

Results and Discussion

Effect of Temperature on Nanofluids Viscosities

The viscosity of the nanofluids was estimated using Einstein’s formula as modified by Drew and Passman for the two-phase mixture (equation 4). It is well known that the dynamic viscosity decreases by temperature increase due to the higher mobility of the ions, based on the Arrhenius equation [33]. The viscosity of nanofluids was studied as a function of temperature within the range of 30°C to 70°C as presented in Figure 2a and 2b. From the figure, it can be observed that the NPs loading slightly affected the viscosity at low temperature. However, this influence diminished by increasing the temperature. On the other hand, the fluids followed Arrhenius behavior at all NPs loadings. Rising the temperature reduced the internal resistance of the molecules, which resulted in easy movement of the flow. Arrhenius equation is considered as a simple expression to describe this behavior, as long as the dependence of temperature on dynamic viscosity is concerned. The data showed identical curves for both DESs at different NPs ratios; however, DES1 showed higher viscosities than DES2. Urea has a higher effect on viscosity than glycerol due to its amide type, which could lead to forming self-hydrogen bonds between the chloride ions and urea [44].

Figure 2a: Viscosity of nanofluid as a function of nanoparticles volume and temperature for DES1.

Figure 2b: Viscosity of nanofluid as a function of nanoparticles volume and temperature for DES2.

Effect of NPs Loading on the Fluid Friction Factor

The friction factor of pure DESs and nanofluids was calculated by equation 6 and its relationship with Reynold number was presented in Figure 3a and 3b for (a) DES1 and (b) DES2. Results showed that the base DES1 had a higher friction factor (2.662) than DES2 (1.382) at the same velocity (2.12 m/s) due to the higher viscosity of DES1, which attributed to the presence of urea [32]. It can be noted, from both figures, that the friction factor decreased by increasing Re number at all NPs ratios. On the other hand, a tiny increase was observed by increasing the NPs ratios, which could be attributed to the high base fluid viscosity (no difference can be observed from the figure). It was reported that the nanoparticles increased the fluid’s viscosity, resulting in a higher friction factor due to the decrease in Re number [45,46]. However, in our DESs system, the friction factor was not affected by increasing the NPs load due to the high viscosity of the DESs. To evaluate our findings, the friction factor of DES1 and DES2 was compared to water at the loading ratio of 2%, with the consideration of different applied flow rates [47]. The friction factor in this study was much higher, which could improve the heat transfer exchange [20]. However, increasing the nanofluids viscosity could agglomerate the nanoparticles, leading to increasing the pumping system power.

Figure 3a: The effect of Reynolds number on nanofluids friction factor for DES1.

Figure 3b: The effect of Reynolds number on nanofluids friction factor for DES2.

Nusselt Number Relationship With Re and Pr Numbers

Nu number can be defined as the ratio of the convective to conductive heat transfer [43], which was calculated by equation 8. Figure 4a and 4b present Nu number as a function of Re number for the DESs at different NPs loadings. The results indicated that the base fluid has a higher Nu number than the nanofluids; Nu number decreased by increasing the NPs ratios but increased with Re number increasing [48]. This is due to the effect of NPs on the density and viscosity of the nanofluid, by which Re number was estimated. Here, as Re number increased by decreasing the viscosity, DES2 had a higher Nu number than DES1. Figure 5a and 5b show the relationship of Nu number with Pr number. Pr number was calculated via Equation 9, where the thermal conductivity was practically measured in this work. The DES1 thermal conductivity was found to be 0.354 ± 0.06, while its value was 0.378 ± 0.07 for DES2. From the figure, DES2 showed higher Nu number than DES1 at the same Pr number. Also, Nu number decreased by NPs loading and Pr number increasing. The maximum Nusselt number was 57.116 for DES1 and 67.442 for DES2 at NPs loading ratio of 0%. Figure 6 illustrates the effect of NPs ratio on Pr number, where DES1 had higher values than DES2 due to its higher viscosity and lower thermal conductivity. By increasing the NPs ratio, Pr number decreased because of the decreasing in the heat capacity and increase in thermal conductivity. It was found that there are many factors might affect the heat transfer process, such as the friction force between the fluid and nanoparticles, Brownian force, agglomeration, and gravity [15].

Figure 4a: Nusselt number vs Reynolds number for DES1.

Figure 4b: Nusselt number vs Reynolds number for DES2.

Figure 5a: Nusselt number vs Prandtl number as a function of nanoparticles volume for DES1.

Figure 5b: Nusselt number vs Prandtl number as a function of nanoparticles volume for DES2.

Figure 6: Prandtl number as a function of nanoparticles volume for DES1 and DES2.

Effect of NPs Loading on Heat Transfer Coefficient

The convective heat transfer coefficient (h) is an important parameter for heat exchangers design. In this report, it was calculated by equation 10 and studied as a function of NPs loading as illustrated in Figure 7a and 7b for DES1 and 2, respectively. The results showed that DES2 had a higher heat transfer coefficient (1699.54 W/m² K) than DES1 (1347.95 W/m² K) as base fluids at a flow rate of 100 L/min. It was observed that the heat transfer coefficient increased by increasing the flow rate (increasing Re number) and decreasing the NPs loading. The maximum heat transfer coefficients were at 0% volume concentration and flow rate of 300 L/min with values of 4043.85 and 5098.63 W/m² K for DES1 and 2, respectively. By adding 5% NPs, these values decreased to be 3495.89 and 4513.73 W/m² K for DES1 and 2, respectively. This decrease attributed to the decrease in Pr number, which decreased by NPs increasing due to the higher heat capacity of the DESs than the NPs. Maiga et al. [49] have numerically investigated the forced convection heat transfer of nanofluids in the laminar flow area in different systems and ended up with conflicting conclusions to ours. This disagreement is because they used water, which had a lower heat capacity than the NPs; while the DESs had much higher heat capacity values. In other studies, it was found that the nanoparticles can affect other physical properties, such as the specific heat, specific mass, and dynamic viscosity [35,50]. It was also found that the convection movement increases proportionally with the NPs density and heat capacity but inversely with the shape factor and thermal conductivity [51,52]. Nevertheless, our findings are in contrast with the general concept of nanofluids, where filling the NPs increase h. Here, it could be concluded that the commonly used equations to calculate the thermal properties are not applicable to fluids of high viscosity and heat capacity. An experimental study is recommended to compare the results and calculate the difference in values.

Figure 7a: Heat transfer coefficient vs NPs loading for DES1.

Figure 7b: Heat transfer coefficient vs NPs loading for DES2.

Conclusion

The thermal conductivity of choline chloride: urea and choline chloride: glycerol was measured and reported in this work. Al₂O₃ nanoparticles dispersion in deep eutectic solvents, flow in a horizontal shell and tube heat exchanger, and heat transfer performance was theoretically investigated using nanofluid correlations. The effect of adding nanoparticles on friction factor, Nusselt number, heat transfer coefficient, and flow behavior were studied. It was found that the pure DESs have higher heat transfer coefficient than their nanofluids, which was attributed to their high heat capacities. Although the DESs have a higher viscosity than water, which requires a high-pressure pumping system, DESs is still recommended to use, especially at high temperatures, due to their unique properties. By injecting 5 vol% NPs at a flow rate of 300 L/min, the heat transfer coefficient decreased from 4043.85 and 5098.63 W/m² K to 3495.89 and 4513.72 W/m² K for DES1 and 2, respectively. The nusselt number for DES1and 2 also decreased from 57.12 and 67.44 to 46.61 and 56.42, respectively, when the pure DESs loaded by 5% NPs. Finally, the friction factor wasn’t affected by NPs concentration increasing due to the high viscosity.

Acknowledgment

We like to greatly acknowledge the Higher Committee for Education Development in Iraq (HCED-Iraq) for supporting this work. Also, we like to thank Dr. Muthanna Al-Dahhan in the Chemical Engineering Department at Missouri University of Science and Technology for providing access to his lab to conduct the thermal conductivity test.

References

1. Taylor R, et al. Small particles, big impacts: A review of the diverse applications of nanofluids. J Appl Phys. 2013;113:1-19.
2. Choi SUS and Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. ASME International Mechanical Eng Congress and Exposition. 1995.
3. Saidur R, et al. A review on applications and challenges of nanofluids. Renewable and Sustainable Energy Reviews. 2011;15:1646-1668.
4. Botha SS. Synthesis and characterization of nanofluids for cooling applications. South African Institute for Advanc Materials. 2007.
5. Lee J. Convection performance of nanofluids for electronics cooling. Stanford University, USA, 2009.
6. Naphon P, et al. Numerical investigation on the heat transfer and flow in the mini fin heat sink for CPU. Int Commun Heat Mass Transfer. 2009;36:834-840.
7. Nguyen C, et al. Heat transfer enhancement using Al₂O₃ water nanofluid for an electronic liquid cooling system. Appl Therm Eng. 2007;27:1501-1506.
8. Wang R. Refrigerating system using HFC134a and mineral lubricant appended with n-TiO2(R) as working fluids. 4th Int Symposium on HAVC. Tsinghua University Press, China. 2003.
9. Wu S, et al. Thermal energy storage behavior of Al₂O₃-H2O nanofluids. Thermochim Acta. 2009;483:73-77.
10. Kuo K, et al. Potential usage of energetic for nanosized powders for combustion and rocket propulsion. Mater Res Soc Proc. 2004;800:3-14.
11. Kulkarni D, et al. Application of aluminum oxide nanofluids in diesel electric generator as jacket water coolant. Appl Therm Eng. 2008;28:1774-1781.
12. Yang Y. Carbon nanofluids for lubricant application. University of Kentucky, USA. 2006.
13. Naphon P, et al. Experimental investigation of titanium nanofluids on the heat pipe thermal efficiency. Int Commun Heat Mass Transfer. 2008;35:1316-1319.
14. Hussein AM, et al. Study of forced convection nanofluid heat transfer in the automotive cooling system. Case Studies in Thermal Eng. 2014;2:50-61.
15. Vishwanadula H and Nsofor EC. Studies on forced convection nanofluid flow in circular conduits. ARPN J of Engineering and App Sci. 2012;7:371-376.
16. Xuan Y and Li Q. Heat transfer enhancement of nanofluids. Int J of Heat and Fluid Flow. 2000;21 :58-64.
17. Kwak K and Kim C. Viscosity and thermal conductivity of copper oxide nanofluid dispersed in ethylene glycol. Rheol. 2005;17:35-40.
18. White SB, et al. Investigation of the electrical conductivity of propylene glycol-based ZnO nanofluids. Nanoscale Res Lett. 2011;6:1-5.
19. Wang XQ and Mujumdar AS. Heat transfer characteristics of nanofluids: A review. Int J of Thermal Sci. 2007;46:1-19.
20. Abbott AP, et al. Novel solvent properties of choline chloride/urea mixtures. Chem Commun. 2003;1:70-71.
21. Kadhom MA, et al. Studying two series of ternary deep eutectic solvents (Choline Chloride-Urea-Glycerol) and (Choline Chloride–Malic Acid–Glycerol), Synthesis and Characterizations. Arabian J for Sci and Eng. 2017;42:1-11.
22. Zhang Q, et al. Deep eutectic solvents: syntheses, properties and applications. Chem Soc Rev. 2012;41:7108-7146.
23. Abbott A and McKenzie K. Application of ionic liquids to the electrodeposition of metals. Phys Chem Chem Phys. 2006;8:4265-4279.
24. Abbott A, et al. Application of hole theory to define ionic liquids by their transport properties. J Phys Chem B. 2007;111:4910-4913.
25. Francisco M, et al. Low-Transition-Temperature Mixtures (LTTMs): A new generation of designer solvents. Angew Chem Int Ed. 2013;52:3074-3085.
26. RuB C and Konig B. Low melting mixtures in organic synthesis-an alternative to ionic liquids. Green Chem. 2012;14:2969-2982.
27. Martis P, et al. Electro-generated nickel/carbon nanotube composites in ionic liquid. Electrochim Acta. 2010;55:5407-5410.
28.  Abbott A, et al. The electrodeposition of silver composites using deep eutectic solvents. Phys Chem Chem Phys. 2012;14:2443-2449.
29. JD Mota-Morales, et al. Synthesis of macroporous poly(acrylic acid)-carbon nanotube composites by frontal polymerization in deep-eutectic solvents. J Mater Chem A. 2013;1:3970-3976.
30. Fang YK, et al. Synthesis and thermo-physical properties of deep eutectic solvent-based graphene nanofluids. Nanotech. 2016;27:1-10.
31. Hamad AA, et al. Potential applications of deep eutectic solvents in nanotechnology. Chem Eng J. 2015;273:551-567.
32. Abdullah G and Kadhom M. Studying of two choline chloride’s deep eutectic solvents in their aqueous mixtures. Int J of Eng Research and Development. 2016;12:73-80.
33. Abbott AP, et al. Glycerol eutectics as sustainable solvent systems. Green Chem. 2011;13:82-90.
34. Leron RB and Li MH. Molar heat capacities of choline chloride-based deep eutectic solvents and their binary mixtures with water. Thermochimica Acta. 2012;530:52-57.
35. Pak BC and Cho YI. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Experimental Heat Transfer. 1998;11:151-170.
36. Xuan Y and Roetzel W. Conceptions for heat transfer correlation of nanofluids. Int J of Heat and Mass Transfer. 2004;43:3701–3707.
37. Yu W and Choi SUS. The role of interfacial in the enhancemened thermal conductivity of nanofluid: a renovated Maxwell model. J of Nanoparticles Researches. 2003;5:167-171.
38. Drew DA and Passman SL. Theory of multi component fluids. Appl Mathematical Sci. 1999.
39. Chandrasekar M, et al, Experimental studies on heat transfer and friction factor characteristics of Al₂O₃/water nanofluid in a circular pipe under laminar flow with wire coil inserts. Experimental Thermal and Fluid Sci. 2010;34:122-130.
40. Rott N. Note on the history of the Reynolds number. Annual Review of Fluid Mech. 1990;22:1-11.
41. Seider E and Tate G. Heat transfer and pressure drop of liquid in tubes. Ind Eng Chem. 1936;28:1429–1435.
42. White FM. Viscous fluid flow. New York: McGraw-Hill. 2006.
43. Incropera F, et al. Fundamentals of heat and mass transfer. Hoboken: Wiley. 2002.
44. Y Liu, et al. Synthesis and characterization of novel ternary deep eutectic solvents. Chin Chem Lett. 2014;25:104-106.
45. Gnielinski V. New equations for heat and mass transfer in turbulent pipe and channel flow. Int Chem Eng. 1976;16:359-368.
46. Duangthongsuk W and Wongwises S. Heat transfer enhancement and pressure drop characteristics of TiO2–water nanofluid in a double-tube counter flow heat exchanger. Int J of Heat and Mass Transfer. 2009;52:2059.
47. Albadr J, et al. Heat transfer through heat exchanger using Al₂O₃ nanofluid at different concentrations. Case Studies in Thermal Eng. 2013;1:38-44.
48. Luciu RS, et al. Nusselt Number and Convection Heat Transfer Coefficient for a Coaxial Heat Exchanger Using Al₂O₃-Water pH=5 Nanofluid," Politehnic Institute Bulletin of IAS. 2009;2:71-80.
49. Maiga SEB, et al. Heat transfer enhancement by using nanofluids in forced convection flows. Int J of Heat and Fluid Flow. 2005;26:530-546.
50. Ho CJ, et al. Natural convection heat transfer of alumina-water nanofluid in vertical square enclosures: an experimental study. Int J of Thermal Sci. 2010:49;1345-1353.
51. Kim J, et al. Analysis of convective instability and heat transfer characteristics of nanofluids. Phys Fluids. 2004;16:2395-2401.
52. Roy G, et al. Numerical investigation of laminar flow and heat transfer in a radial flow cooling system with the use of nanofluids. Superlattices Microstruct. 2004;35:497-511.