Research & Reviews: Journal of Ecology and Environmental Sciences
MenuISSN: 2347-7830
ISSN: 2347-7830
+44-7723-59-8358 Faculty of Sciences of Tunisia, Laboratory of Genetics Populations and Biometry, Tunis, Tunisia
Received Date: 28/08/2017; Accepted Date: 29/09/2017; Published Date: 07/10/2017
Visit for more related articles at Research & Reviews: Journal of Ecology and Environmental Sciences
In the present work, a mathematical model for the raw data collected from the cultures of Fabaceae has been proposed and analyzed after they have submitted to the allelopathic effect of existing substances in the leaf extract of Eucalyptus gomphocephala. This model has been treated while putting into consideration the abiotic conditions and the number of repetitions in the plot factors. If allelopathy, where a species produces toxic and affects the other, we see that the species can be made to disappear if the dose of these substances appears high.
Alleopathy, Leaf extract, Mathematical model, Alleopathic effect
Plants have an important role in the evolutionary dynamics of populations and the functioning of ecosystems in addition of their role in the setting of nutrient and water resources in the ground and thus contribute to the inhibition of the evaporation and infiltration [1,2]. They also have enormous capacity to change the properties of specific plants, which are forest species whose action is to deplete the soil in producing toxic entities preventing herbaceous develop in their territories [3]. Eucalyptus is a very rich species in secondary metabolites, which are likely to play an important role in biotic relationships. It has been shown that the effects of Eucalyptus have called "allelopathic interactions," that is, they produce exudates from leaves and roots preventing the growth of other plants. Several experiments have shown that some grasses grew poorly in litters of Eucalyptus in Congo. Other studies in the same plantations emphasized instead a "catalytic" of Eucalyptus plantations allowing woody and herbaceous species native to relocate (Newsletter, members of the Network International Tropical Trees, 1999) effect. The allelochimicals composites act on various levels; the most interesting are the cellular and the biochemical level. These entities act through different channels such as the inhibition of cell division and as well as protein synthesis elongation, changes in membrane permeability and mineral absorption, changes in photosynthesis and respiration, or yet by a negative interference with growth hormones. They can also influence the biological nitrogen fixation, reducing the number and size of nodules [4,5]. The phenomenon of spontaneous regeneration and cultivated species is recognized as an important component of forest management in general. Field studies are usually combined with mathematical models as the most effective way to understand and predict the natural regeneration average [6]. Different are the jobs that have been interested in studying the deterioration of biodiversity in terrestrial ecosystems using a mathematical model [7-15]. The conceptual framework underlying most models can be reviewed in the light of recent efforts to describe the importance of vegetation dynamics in the evolution of weather patterns. It is unlikely that any single approach to modeling will prove sufficient for modeling natural regeneration in all conditions, and we provided guidance on how to create models of effective regeneration [7]. The present work consists of an estimate of the allelopathic power of Eucalyptus gomphocephala through the effect of leaf extracts of three leguminous crops namely Medicago sativa, Vicia sativa and Pisum sativum using a matrix and polynomial mathematical modeling, in this context, lines crop environment have been made to scrutinize this effect at two vegetative stage and reproductive stage of these legumes.
Three species belonging to the Fabaceae family interest in this study are: alfalfa (Medicago sativa ssp sativa) common vetch (Vicia sativa ssp sativa) the pea (Pisum sativum ssp sativum). The seeds were obtained from the Seed Analysis Laboratory of the Tunisian Ministry of Agriculture, Water Resources and Fishing. These seeds were harvested in 2010 and put into storage in a cold room until use. Eucalyptus leafs were collected between the months of November and December 2011. After placing in an oven at a temperature of 60°C for 5 days, the leaves were subjected to fine grinding to recover a quantity of powder. The Eucalyptus species chosen in this study is Eucalyptus gomphocephala: This choice is based primarily on the availability of plant material, the resistance of this species to parasitic infections. Following the phase of germination in Petri dishes, germinated seeds were planted in pots at the plot in a semi -random distribution after a draw. The experimental design adopted the following experimental model blocks. The planting was carried out in 360 pots over 4 blocks and each block contains 30 repetitions for each variety. The concentrations used in the experiment are summarized in the following Table 1.
Table 1. Concentrations used throughout the experimentation.
| Bloc | Concentration | Powder’s quantity putted (mg) |
|---|---|---|
| 1 | 0% | 0 |
| 2 | 0.025% | 40 |
| 3 | 0.25% | 400 |
| 4 | 2.5% | 4000 |
Prerequisites Selected for the Proposal of a Mathematical Model
The mathematical model we want to highlight it must meet several prerequisites that exist in the environment: the time interval between two successive treatments, the culture surface, the amount of plant powder put in pots and the number of repetitions for each legume species. We also consider the effect of allelochimicals is irreversible sense of Eucalyptus plant target, unlike other proposed models as is the case of the proposed model which established a reversible mathematical model [15].
Interpretation of the Proposed Mathematical Model
We consider “A” the matrix of concentrations of allelopathic substances released into the soil, this matrix can be written as follows (A-1 is the inverse of A, calculated by the Matlab mathematical software).
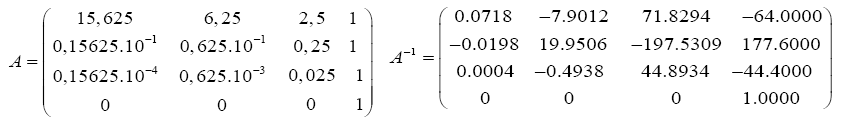
Considering measurability (Ӷ) measured in different periods (S) which depends on the concentrations (x) of the Eucalyptus plant powder. The averages of the measures are in the form of vector systems, as these matrices are inverted using the matlab software:
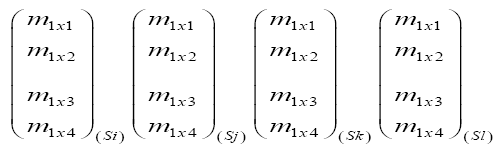
Taking the example of the character Ӷ "plant height" in the specie Medicago sativa:
We make use of polynomials of order 3, since we used four different concentrations of powder or "P" the following polynomial:
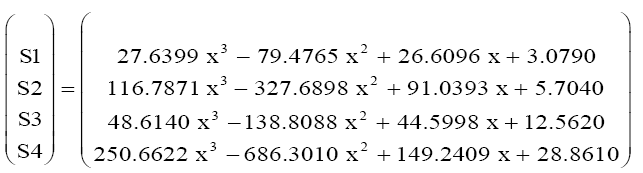
Or "B" matrix following weeks:
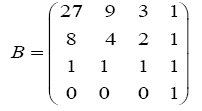
We can write the polynomial "P" above as follows:
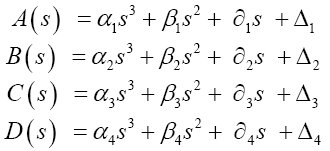
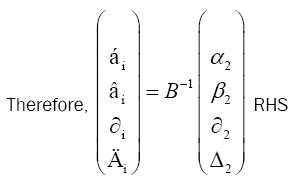
Finally, there will be a polynomial in two variables “x” and “s”, “s” is the week and “x” is the concentration.
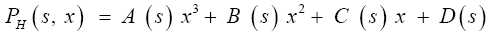
This equation allows us to determinate the coefficients A, B, C and D are the averages in a week if we put into consideration the concentration of vegetable powder x.
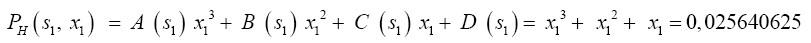
In the same way, we calculate other concentrations for the whole treatment period, there will be the following polynomial coefficients (Table 2).
Table 2. Polynomial coefficients concentrations and their relationships with the stem elongation in three species.
| Weeks | T0 | T1 | T2 | T3 |
|---|---|---|---|---|
| Week 1 | 0 | 0 | 0 | 0 |
| Week 2 | 0.1025625 | 0.07692188 | 0.05128125 | 0.02564063 |
| Week 3 | 1.3125 | 0.984375 | 0.65625 | 0.328125 |
| Week 4 | 97.5 | 73.125 | 48.75 | 24.375 |
Increasing the concentration of the powder in the pot makes stem elongation increasingly reduced (Figure 1). So, allelopathic entities have exercised a retarding effect on stem elongation for Medicago sativa showed a significant decrease in the length of the rod under the effect of Eucalyptus treatments (Figure 2).
Figure 1: Curve shape of the stem height in Medicago sativa using the polynomial coefficients (A) and using the actual measured values (B).
Figure 2: Shape of the curve of the height of the rod in Pisum sativum using the polynomial coefficients (A) and using the actual measured values (B).
In all scenarios, the elongation decreases almost by half, regardless of the time factor, whatever the week studied, the accuracy of the results is demonstrated by a statistical test (p<0.001 by post-test ANOVA, Tukey).
Similarly, we study agromorphological other parameters that depend on the concentration and time of treatment, including reproductive and discontinuous characters as the weight of 100 seeds characters, number of seeds per pod and dry weight vegetative (Figure 3).
Figure 3: Shape of the curve of the height of the rod in Vicia sativa using the polynomial coefficients (A) and using the actual measured values (B).
This work is an assessment of allelopathic power Eucalyptus gomphocephala through the effect of leaf extracts at different stages of germination and growth of three leguminous crops: Medicago sativa, Vicia sativa and Pisum sativum. In this context, germination tests and pipes culture at a plot were made. LC of the powder, Eucalyptus gomphocephala was homogeneously mixed with the peat to achieve concentrations respectively ranging from 0.025 to 2.5% (w/w) powder relative to the total weight of the pot. It appears that from 0.025 to 2.5% (w/w), Eucalyptus may act by reducing the length of the radicle, the average elongation rate and the final germination, and this concentration dependent manner. On the other hand, Eucalyptus is also in the reproductive behavior of plants studied. This was realized by counting flowers, pods and evaluation of performance criteria: number of seeds per pod and 100 seed weight. The advantage of mathematical modeling is a prediction of the evolution of such a character as a function of time as the experiment fails at this late stage of development. One of the limitations of mathematical modeling affected in this work is that it does not describe significantly the evolution of measurability (Ӷ) at the first two weeks. The evolution of such a character appears negligible when compared to the development of the latter with respect to time. Researchers rely in this situation to change variables to demonstrate that early evolution.