Multichannel Nodes With Identical Time of Service and the Transform of Laplace Andrey

Abstract

The current review was subjected to detailed investigation of nodes associated to the device. As per the theorem 2.1 the outcomes were generalized for the series in multichannel nodes leading to estimation of the virtual time of wait for the inlying nodes. Concluding for further investigation in concordance notions of even and odd function with the results of lemma 3.1 and theorem 3.1.

Keywords

Nodes; FIFO; Customers; Y1 condition

Introduction

In the [1,2] works of author the nodes with one device in every node were explored. In the second section of the work the results are generalized in case of multichannel nodes in series (the theorem 2.1) In the 2.1 theorem a new estimation of the virtual time of wait for the inlying nodes is considered. From the estimation the estimation of time of wait ensues too. A primary aim of the work is the proof of the fact, that the very big decrease of total work in inlying nodes is executed not only for one (the [1,2] works), but also for a few devices in one node in conditions of critical load and in conditions of overload (>1) on the first node. An estimations of the theorem 2.1 with C(N)=2N-1; Vⁱ_t Δ(t)(2N-1)=/N are new (in the [3] work the similar theorem is only partly proved; the proof of the 2.1 theorem substantially shorter and simpler than in the [3] work). In particular, the time of wait in the node with the I number (Vⁱ_t i >1, a determination further) and the total time of work (in sum) on all nodes except the first are limited by a small constant, if on the first node the customers arrive with the limited maximal length. From the proof of the 2.1 theorem we get the simple similar theorem for all the service disciplines” without an interruption of service” in every node (the theorem 2.2).

Especially the interesting applications of results of the article follow from the example of conclusion in the case of the determined time of service, when time of service by one device of any customer is equal to constant (for instance, the quantity of customers no more 3 for two devises in every node).

We will mark, that in difference from the first works on the theme of identical service [4,5] all the theorems of the second part of article are proved a. s. for all input processes on the first node (without some limitations on the input process A(t)).

In the second part of the article we consider the regularity of the double transform of Laplace (the first part of theorem 3.1, [ 6]).The task was formulated to the author by the professor Solovjev A.D. in connection with the problem of moments. The theorem proved in this part has a general mathematical character and are easily checked up. With help of the first and second part of the theorem it is simply to prove a some facts related with the transform of Fourier and Laplace (for instance, about the inverse operator of the transform of Laplace, using only positive values of the transform of Laplace on the [0,+∞); all results of third of part are new and belong to the author of the article, some results in the direction were formulated in the [7] works; in the articles the second part of theorem is partly proved). In the 3.1 theorem we use the only well-known mathematical facts. In opinion of author the theorem is interesting on itself too.

The identical service

In the main second part of the article we consider the consistently united nodes with the identical service: the length of service by one device of any customer is identical for every node and every device, or

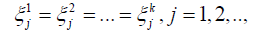
Where the random value 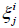is the time of service of customer with the j number on the node with the I number by one device (unit of service), if the service takes place without interruption; the different devices on every nodes are identical, where 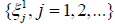are mutually independent random values with the distribution function 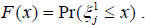Further we will use for 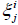the term” length of customer” too.

We consider K nodes, K ≥ 2. The arrival process for node with the j number is equal to the output process on the node with the (j −1) number, j=2,...K.

As soon as the service is finished the customer arrives on the next node. In the 2.1 theorem the customers are served in order of arrival in every node (the FIFO(FCFO) discipline of service), in the 2.2 theorem the order of service is definite before the theorem with help of the D1, D2 conditions. If a customer’s arrives on the first node in a group (for non-ordinary A(t) process), the customers are disposed in the group in a random order all results of the 2.1, 2.2 theorems do not rely on a order in the group. The node with j number consists of N service units (devices) with infinite quantity of wait places, j=1,...K.

In the article we consider the random values:

W^t_j - the total time of service of all customers at the t moment on the j node, j=1,...,K (the virtual time of wait for one channel at the t moment);

V^t_j - the full time of service of customer arriving on the j node at the t moment (on the node with the j number), j=1,...,K (the time of wait plus the ”length of the customer”).

By definition, A(t) is the final customer number among all customers arriving on first node during [0,t] . (If a customer arrives on the first node in a group, the customers are disposed in the group in a random order).

For the ordinary process

A(t)=ma:tk ≤ t, A(t)=0, if t₁>t,

where t_k is the moment of arriving on the first node of the customer with n number.

The process A(t) and the { ξⁱ_j , j=1,2,...} sequence are mutually independent (for all t).

Let ν⁰_j=0, for all j=1,...,K.

In the theorem 2.1 we consider N>1 devices in every nodes, and the customers are served in order of arrival in every nodes.

Theorem 2.1

Proof

We introduce a new Qj(N) system on the node with the j number with help of the S1 and S2 conditions, j=1,...,K.

By definition, the A(j,t) value is equal to the number of the last customer arriving on the node with the j number during [0,t], A(1,t)=A(t), j=1,...,K.

The S1 conditions

For the Q_j(N) system the arrival process is equal A(j,t),j=1,2,...,K, as in main node with j number. The “length of customer” of every customers in the Qj(N) system equals to the lengths for the main system .

The S2 conditions

The speed of service in the Qj(N) system is N (the node with the j number of the Qj(N) system contains 1 device, and the speed of work on the device is N), j ≥ 1.

By definition, W^t_j is a sum of remaining ”lengths of customers” on the node with the j number at the t moment for the Qj(N) system (some of remaining lengths are equal to the complete lengths) with the primary input process on the node with the j number.

By definition, for primary system (not for Qj(N) system) 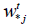is the total sum of full ”lengths of customers” on the node with the j number at the t moment, 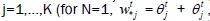by definition, 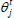is the part of the “length of customer” is already served at the t moment in the primary system on the j node,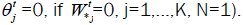

It is simply to check, that for N>1 the

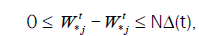(1)

inequality takes place for all t, if the input process on the node with the j number is the same for the primary and the Qj(N) systems. To obtain the fact we can consider the 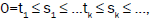points on the axis of time, where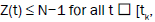 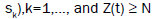for all 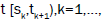by definition, Z(t) is the total number of the working devices in the node with the j number for the primary system (all the processes are continuous on the right). It is obviously, 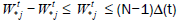for all t 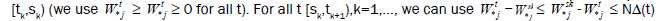(the speed of service in the primary system is equal to N, and the speed of service in the Qj(N) system is N or 0, if 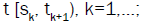if a customer arrives on the next node at the 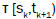moment, one remaining length is substituted by other at the τ moment. We used the methods of the lemma 2.2 in the [8,9] articles too.

From the definitions of the 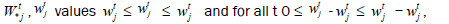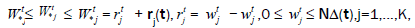(2)

with help of the (1) inequality.

We will estimate the 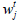value for j ≥ 2.

One device works in the Qj(N) system; the speed of work in the Qj(N) system is equal to N from the S2 conditions, and we can use Borovkov ([10], p.41)

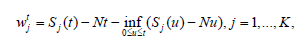(3)

where Sj(u) is the total sum of lengths of service of customers (the total sum of ”lengthes of customer”) arriving on the node with the j number during [0,t].

From the definition of the wt j characteristics we get

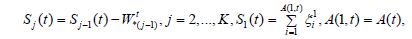
and from (2)

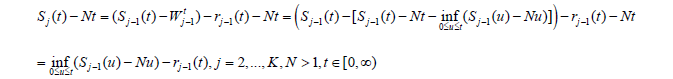
After substitution in (3) we get

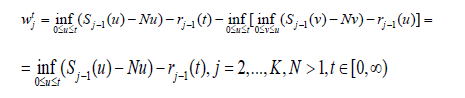
where in the last inequality we use

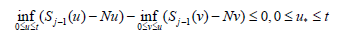
From 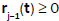and (2) we obtain

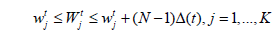
We can use 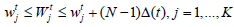(we use the lemma 2.2 in the [9] article, or the fact is easily checked up directly after breaking of axis of time up on intervals by the 0 ≤ s₁ ... ≤ s_k ... points too). We get

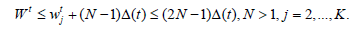
For wt j the theorem 2.1 is proved.

By definition, the customer with the n(t) number arrives in the node with the j number at the t moment.

If 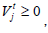we obtain the

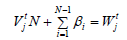
equality, where 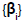are some remaining ”lengths of customers ” in the moment of beginning of service of customer with the n(t) number. We get 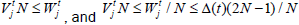(with help of

In the theorem 2.2 we consider all disciplines of service “without an interruption of service”: the customers are served by the units of service of every nodes without an interruption (the precise definition is in the D1,D2 conditions).

To determine the disciplines we shall use the D1, D2 conditions.

Condition D1

The speed of service is the 1 for any unit of service, if the unit works. Exactly, in the node with the j number the quality of working units is min (N, d ∈)G at the t moment.

Condition D2

If the customer arrives to some unit of service, the customer is served by the unit of service without interruption until the moment, when the customer leaves the node. By definition, d ∈G if for the service discipline d the D1 and D2 conditions take place.

Theorem 2.2

Let the d_j,j=1,...,K, disciplines handle by the process of service in the node with the j number, and d_j ∈ G,j=1,...,K, N ≤ 1.

For 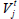takes place all the results of the theorem 2.1, j=2,...,K, t ∈ [0,∞). (Not for the 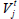values).

Proof

The proof of the 2.2 theorem word for word repeats proof of theorem 2.1 (in proof of the 2.1 theorem the FIFO(FCFO) discipline was not used).

3. The regularity of Laplace transform in |z|<a>0.

For the u(p) function we use the Y1 condition.

The Y1 condition

The Y1 condition takes place, if the u(p) function is regular as in{p:|Imp|<A} so as in |Rep|<B} for some A ∈ (0,+∞),B ∈ (0,+∞), u(0)=0, and |u(p)||p|2+δ → 0,|p|→ ∞,δ>0, δ=const., in the {p:|Imp|<A}, {|Rep|<B} areas .

By definition,

Theorem 3.1

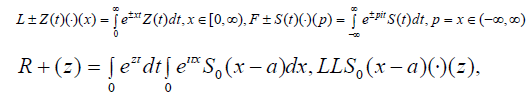
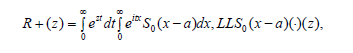
functions are regular in the area z:|z|<2a>0, if for the S₀(p) function the Y1 condition takes place with the B=A=2a constants. If instead of S₀(p−a) we use S(p)=S₀(p−a), the R+(z),LLS(x)(·)(z) functions are regular in |z|<a, if the Y1 condition takes place for the S(p) function with A=B=3a>0.

ImLF+{u}(is) ≡ 0,s ∈ (−∞,∞),

if for the u(p) function the Y1 condition takes place for some A>0,B>0.

Proof

We will prove the first part of the theorem, [6].

In the integral

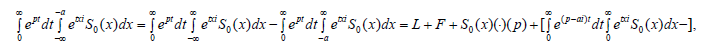
the first part of the sum is regular in the |Rep|<2a area, if the S₀(−z) function is regular in |Imp|<2a (the fact is well-known, [11, 12]).

The second part of the sum together with the integral (it is obviously, we can change the limit of integration, if Rep<0,[14]) 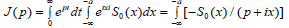is regular for all p:Imp ∈ (-a,+∞), a>0 (the integral obviously has dJ(p)/dp in the area, and the integral in the form is regular in 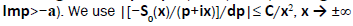in the small area of the p point, [13,14].

We obtain, that the second part of the sum 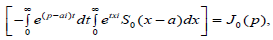is regular for all z=p−ai:Imp ∈ (−a,+∞)∩{|Rep|<2a}, or for the all G₀={z:Imz ∈ (-2a,+∞)∩{|Rez|<2a}}, where |z|<2a ∈ G0. The e the second equality of the first part of the 3.1 theorem we obtain now from LLS₀(x−a)(·)(iu)=(-i)R+(−u),u ∈ (0,+∞), [13].

The first part of the theorem 3.1 is proved.

We will prove the second part of the theorem 3.1, [15].

From the

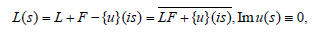
s ∈ (−∞,∞), equality we obtain

ImL(s)=−Iml(s),l(s)=LF+{u}(is),s ∈ (−∞,∞),

We will prove, that the similar equality takes place with other sign.

We can consider the fractionally-linear represent ([13])

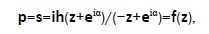
α,h,∈ (0,+∞). The f(z) function represents {z:|z|≤ 1}=S → G+, where G+={p:Imp ≥ 0} ([13], p.128), such that the C₁={w:|w|=1} circumference transfers in the (−∞,∞) line: C1→(−∞,∞), f(w)=s, s ∈ (−∞,∞),|w|=1. We obtain

L(f(w))=L(s),

for all |w|=1,s ∈ (−∞,∞).

From the l(p)=LF+{u}(ip),Imp ≥ 0, definition we obtain the new l(f(z)) function:

S → G−={p:Imp ≤ 0},

such that C₁ → (−∞,∞). We will mark, that the real part of the new l(f(z)) function on the (−∞,∞) is the same as the real part of the old L(f(p)) function on the same (−∞,∞) axis:

ReL(f(w))=Rel(f(w)),|w|=1,

from the equalities ReL(s)=Rel(s),s ∈ (−∞,∞), s=f(w),|w|=1.

The complex parts of the two L(f(z)),l(f(z)) functions are the same ImL(f(z))=Iml(f(z))+c_*,|z|=1, functions (as the only decision of the Dirichl´et problem in |z|≤ 1, [13], p. 209).

Before it was marked ImL(s)=−Iml(s)):

ImL(s)=ImL(f(z))=Iml(f(z))=Iml(s),

f(z)=s ∈ (−∞,∞),|z|=1, (it is obvious, c_*=0 from

L(s) → 0, s →±∞,

in the Y1 conditions).

We use, that both L(f(z)), l(f(z)) are regular in |z|≤ 1, the functions are continuous on the |z|=1 from the |z|<1 side, and

L(p₁) → 0,p₁ →∞,

if Rep₁ ≤ 0,

l(p₁) → 0, p₁ →∞,

if Rep₁ ≥ 0,[13,14] (see the definition of the f(z) function in [13], p. 127 too).

The last the L(p₁) → 0, l(p₁) → 0, z → e^iα, equalities we obtain from

l(p₁)=C(0)/p₁+(i/p₁)LF+{xu(x)}(p₁) → 0, p₁ →∞,

Rep₁ ≥ 0, C(0)=const.,|C(0)|<∞, from

|F+{xu(x)}(t)|=|(1/t²)F+{d²(xu(x))/dx²}(t)|≤ c₁/t², t → ±∞, c₁=const., c₁<∞, with help of the formula of the integration by parts (we use the Y1 condition for the u(x) function too).

From the ImL(s)=Iml(s), ImL(s)=−Iml(s), s ∈ (−∞,∞) equalities we obtain ImL(s)=0, s ∈ (−∞,∞).

The second part of the theorem 3.1 is proved.

From the first part of the theorem 3.1 we get the lemma 3.1.

Lemma 3.1

In the conditions of the first part of the theorem 3.1 R₁(−p)=−R₁(p),p ∈ C, where R₁(p)=LCo(S(x))(·)(p), S(−x)=S(x),x ∈ (−∞,∞); R₂(−p)=R₂(p),p ∈ C, where R₂(p)=LSi(S(x))(·)(p), S(−x)=−S(x),x ∈ (−∞,∞), [3,6, 12].

Conclusions

In example the most interesting application of the 2.1 theorem is considered in the case of the determined service in every node.

Example 4.1. We consider K consistently located devices with identical service, N>1. The total quality of customers on every node with numbers j>1 is not more 2N−1 (not more 1, if N=1, [1]), if the time of service of every customer by every device is the m constant for every nodes :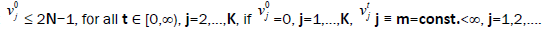 By definition, v^t_j is the total quality of customers on the node with the j number at the t moment.

We will mark also, that the results of the third paragraph require the further study in the direction of concordance notions of even and odd function with the results of lemma 3.1 and theorem 3.1.

Acknowledgment

The author marks an of principle role of my teacher professor Solovjev A.D. (1927-2001) in appearance of the work (on the seminar from the department of the theory of probability in Moscow University nam. Lomonosov in the laboratory corps A at 1977- 1993 y.)

References

1. V. Pavlov. Diffusion approximations and variation of conditions of ergodicity for identical service. Advan.Math.Scien.1997;52:171 - 172.
2. Andrey Valerianovich Pavlov. A net with serial access and the reduction of total work for identical
3. Service. Publ. in Intern. Academic Press, Statict., Optimiz., Inform., Comput. 2017; 5:121-126.
4. A. V. Pavlov. The disciplines of service with prior to the shortest and identical ser-vice, MGTUREA(MIREA). 2013;119.
5. O. J. Boxma. On a tandem queueing model with identical service time at both counters. I,II, Ad-van.Appl.Probal. 1979;11: 616 – 659.
6. O. J. Boxma. Q Deng, Asymptotic behavior of tandem queueing system with identical service times at both queues, Springer Publishers, Math. meth. of oper. res. 52:307 - 327, 2000.
7. Andrey Pavlov V. Identical service and the odd or even transform of Laplace, Moscow University nam M.V. Lomonosov, RUDN., Conferen. Anal. and comp. meth. in probab. theor. and its appl., (ACMPT2017), 23-27 okt. Moscow pp.31-35, 2017.
8. A. V. Pavlov. About the equality of the transform of Laplace to the transform of Fourier, Issues of Analysis. Petrozavodsk; 23: 21-30, 2016.
9. V. Pavlov. The asymptotically optimal disciplines of service for some multi-channel networks, Theory Probab. and Appl. Moscow; 36:170 -175, 1991.
10. V. Pavlov. The asymptotically optimal disciplines of service in the conditions of heavy traffic, Theory Probab. and Appl. Moscow ; 35:713-727,1990.
11. A. Borovkov. The stochastic process in a theory of service, Science, Moscow. 367,1972.
12. V. Pavlov. The Fourier transform and new inversion formula of the Laplace transform, Springer Publishers, Math notes. 90:793-796,2011.
13. V. Pavlov. Reliable prognosis of the functions in the form of transformations of Fourier or Laplace, Herald Of Mirea, Mirea (Mtu). Moscow; 3:78-85,2013.
14. M. A. Lavrentiev, B. V. Shabat. The methods of theory functions of complex variable. Science. Moscow; 688,1987.
15. G. M. Fihtengoltz. The course of differential and integral calculus II. Science. Moscow; 800,1969.
16. A. V. Pavlov. The Dirichlet problem and disappearance of the imaginary part of the Laplace transform on the imaginary axis in connection with the Fourier, Laplace operators, RUDN University, Math. Inst. nam. Steklov, The 8th Int. Conferen on Differential and Functional Differential Equations. Moscow.137,2017.