In this paper, an object recognition system is proposed, that provides the best way to recognize the object from the given image. The process of the proposed method is the input given to the system is the color image. First the color image is converted into Gray-scale image using color conversion method. To obtain the important details of the object, canny’s edge detection method is employed. The edge detected image is inverted. From the Inverted image the feature vector is constructed with the following information i) Hu’s Seven Moment Invariants ii) Center of the object iii) dimension of the object. The information stored in the database for each image is eigenvalue generated from the computed feature vector using Principal Component Analysis. K-Nearest Neighbor is applied to the feature vector to recognize the object by comparing the information already available in the database to the eigenvalue of new image. To prove the efficiency of the proposed method the feature vector generated using orthogonal moment is used with K-Nearest Neighbor Method. The K-Nearest Neighbor outperforms well when compared to Fuzzy KNearest Neighbor and Back Propagation Network.
Keywords |
| Canny Edge Detection; Moment Invariant; Nearest Neighbor; Neural Network; Object Recognition;
Principal Component Analysis. |
INTRODUCTION |
| Object recognition is a fundamental problem in computer vision. Recognizing two-dimensional objects from an
image is a well known. Most of the researchers consider the feature information for recognizing the object at either local
or global. Only few evaluated both the local and global feature for the object recognition. Based on the features used for
recognition, feature extraction methods can be broadly divided into two categories: local approaches and global
approaches. Object recognition, which is an easy task for a human observer, has long been the focus of much research in
Computer Vision, as an essential component of many machine-based object recognition systems. A large number of
different approaches have been proposed in the literature. The problem in object recognition is to determine which, if
any, of a given set of objects appear in a given image. Thus object recognition is a problem of matching models from a
database with representations of those models extracted from the test image. In this paper, the given color image is
preprocessed and converted into gery-scale image. The grey-scale image is used for the object recognition process. First
Canny Edge Detection Method is applied to detect the edges. From the edged detected image the Geometric moment
invariant is computed along with the dimension of the object and the center of the object. These computed values
constitute the feature vector. The feature vector is applied Principal Component Analysis to reduce the dimensionality of
the data and to produce the eigenvalue of the image. During the training phase the above process is performed and the
eigenvalue along with the tag is stored in the database. During the testing phase for the given image the eigenvalue is
computed and compared with the value retrieved from the database. Based on the result, a rotation and scaling invariant
function is constructed to achieve a set of completely invariant descriptors. A k-nearest neighbors classifier is employed
to implement classification[18]. |
| Theoretical and experimental results show the superiority of this approach compared with orthogonal moment-based
analysis methods. Also to prove the efficiency of k-nearest neighbor the Fuzzy-k nearest neighbor and back propagation network is used for classification. From the results, it is shown that the k-nearest neighbor performs well compared to
others. |
| The rest of the paper is organized as follows. Section III introduces the overall framework of the proposed method,
which consists of canny’s edge detection, Geometric Moments and Moment Invariants. The Eigen Value computation is
discussed in Section IV. After section IV, Section V describes the classifiers and neural networks used for the
recognition purpose. Section VI provides experimental results and Section VII concludes the paper. |
RELATED WORK |
| J.Gao et.al, suggests the nearest neighbor is the best method for classifications of patterns. Luo Juan and Oubong
Gwun suggests PCA-SIFT plays significant role in extracting the best features for image deformation. LiLi et.al, proves
that the kNN is easier and simpler to build an automatic classifier. Ahmed et.al, states that the importance of the SIFT
keypoints in object identification. Ananthashayana V.K and Asha.V found that the PCA and IPCA plays vital role in
the feature extraction process. Te-Hsiu et.al., proposes the use of eigenvalues of covariance matrix, resampling and
autocorrelation transformation to extract unique features from boundary information and then use Minimum Euclidean
distance method and back propagation neural networks for classification. S. Dudani et.al, shows that moment invariants
plays vital role in aircraft identification. |
PROPOSED WORK |
| The proposed framework consists of two stages i) Training phase and ii) testing phase. During the training phase the
sub-set of images from COIL-100 is given as input to system. In the pre-processing stage the edge is detected in the
image using canny’s edge detection and then the Geometric Moment invariants and the dimensions of the object are
computed. The computer information is formed as feature vector. The dimensionality of the feature vector is reduced
using principal component analysis, from which the eigenvalue of the image is computed. The computed eigenvalue is
stored in the database with tag specifying the object. During testing phase, an image is given to the proposed system,
the edge is detected, and from the edge detected image the feature vector is constructed using the moment invariants
and the dimensions of the object. For the new feature vector the eigenvalue is calculated. k-nearest neighbor, fuzzy knearest
neighbor and back propagation network is used for recognizing the object. |
| A. Canny’s Edge Detection: |
| Canny edge detection [19] uses linear filtering with a Gaussian kernel to smooth noise and then computes the edge
strength and direction for each pixel in the smoothed image. This is done by differentiating the image in two orthogonal
directions and computing the gradient magnitude as the root sum of squares of the derivatives. The gradient direction is
computed using the arctangent of the ratio of the derivatives. Candidate edge pixels are identified as the pixels that
survive a thinning process called non-maximal suppression. In this process, the edge strength of each candidate edge
pixel is set to zero if its edge strength is not larger than the edge strength of the two adjacent pixels in the gradient
direction. Thresholding is then done on the thinned edge magnitude image using hysteresis. In hysteresis, two edge
strength thresholds are used. All candidate edge pixels below the lower threshold are labeled as non-edges and all
pixels above the low threshold that can be connected to any pixel above the high threshold through a chain of edge
pixels are labeled as edge pixels. |
| B. Moment Invariants: |
| Moment invariants are used in many pattern recognition applications. The idea of using moments in shape
recognition gained prominence in 1961, when Hu derived a set of moment invariants using the theory of algebraic
invariants [6]. Image or shape feature invariants remain unchanged if that image or shape undergoes any combination
of the following changes i) Change of size (Scale) ii) Change of position (Translation) iii) Change of Orientation
(Rotation) iv) Reflection. |
| The Moment invariants are very useful way for extracting features from two-dimensional images. Moment
invariants are properties of connected regions in binary images that are invariant to translation, rotation and scale [3].
The normalized central moments (1), denoted by pq are defined as |
 |
| C. Orthogonal Moments: |
| Since Hu introduces the moment invariants, moments and moment functions have been widely used in the field of
image processing. Further research proceeds to the introduction of set of orthogonal moments (e.g. Legendre moment
and Zernike moment), where orthogonal moments can be used to represent an image with the minimum amount of
information redundancy. Legendre moments are used in many applications such as pattern recognition, face
recognition, and line fitting. The Legendre moments were used merely, since it is highly complex in computation and
costly during higher order moments. These orthogonal moments have the advantage of needing lower precision to
represent differences to the same accuracy as the monomials. The orthogonality condition simplifies the reconstruction
of the original function from the generated moments. |
EIGEN VALUE AND PRINCIPAL COMPONENT ANALYSIS |
| In linear algebra, the eigenvectors of a linear operator are non-zero vectors which, when operated on by the operator,
result in a scalar multiple of them. The scalar is then called the eigenvalue (λ) associated with the eigenvector (X).
Eigen vector is a vector that is scaled by a linear transformation. It is a property of a matrix. When a matrix acts on it,
only the vector magnitude is changed not the direction. |
 |
| where det() denotes determinant. When evaluated becomes a polynomial of degree n. This is known as the characteristic
equation of A, and the corresponding polynomial. The characteristic polynomial is of degree n. If A is n x n, then there
are n solutions or n roots of the characteristic polynomial. Thus there are n eigenvalues of A satisfying the equation, |
 |
CLASSIFIERS |
| In pattern recognition, the k-nearest neighbor algorithm (k-NN) is a method for classifying objects based on closest
training examples in the feature space. The k-nearest neighbor algorithm is amongst the simplest of all machine learning
algorithms: an object is classified by a majority vote of its neighbors (k is a positive integer, typically small). If k= 1,
then the object is simply assigned to class of its nearest neighbor. The nearest-neighbor method is perhaps the simplest of
all algorithms for predicting the class of a test example. The training phase is simple, ie., to store every training
example, with its label. To make a prediction for a test example, first compute its distance to every training example.
Then, keep the k closest training examples, where k ≥ 1 is a fixed integer. This basic method is called the k-NN
algorithm. For example k=3. when each example is a fixed-length vector of real numbers, the most common distance
function is Euclidean distance |
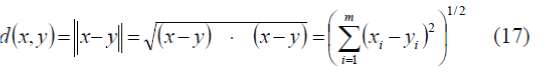 |
| where x and y are points in Rm. |
| A. K-Nearest Neighbor |
| K-Nearest Neighbor algorithm (KNN) is part of supervised learning that has been used in many applications in the
field of data mining, statistical pattern recognition and many others. KNN is a method for classifying objects based on
closest training examples in the feature vector. An object is classified by a majority vote of its neighbors [11]. K is
always a positive integer. The neighbors are taken from a set of objects for which the correct classification is known. It is usual to use the Euclidean distance, though other distance measures such as the Manhattan distance can be used. The
algorithm for computing the K-nearest neighbors is as follows: |
| 1. First determine the parameter K = number of nearest neighbors. |
| 2. Calculate the distance between the query-instance and all the training samples. For distance estimation,
Euclidean distance method is used. |
| 3. Sort the distance for all the training samples and determine the nearest neighbor based on the K-th minimum
distance. |
| 4. Get all the categories of the training data for the sorted value which falls under K. |
| 5. Use the majority of nearest neighbors as the prediction value. |
| B. Back-Propagation Neural Network |
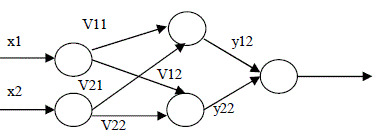
| A Back-Propagation neural network (BPN) consists of at least three layers of units: an input layer, at least one
intermediate hidden layer, and an output layer as Fig. a. Typically, units are connected in a feed-forward fashion with
input units fully connected to units in the hidden layer and all the hidden units fully connected to units in the output layer
[9] |
| The purpose of using Back-Propagation neural network in this study is to adopt the characteristics of memorizing and
referencing properties that recognize the testing 2D image feature [4]. The input of the network is the feature information
extracted from the image. And the target is the designated index of the object. When training the BPN, the input pattern
(x1,x2) is fed to the network, through the hidden layers to the output layer. The output pattern is compared with the
target pattern to find the deviation. These extracted features are continuously fed into a BPN and the network will selfadjust
until a set of weights (V11, V12, V21, and V22) with specified error value. Then these weights are stored and
used for recognition later on. |
| C. Fuzzy K-Nearest Neighbor (K-NN) classifier |
| The fuzzy K-NN is proposed to solve the classification problem by using fuzzy set theory. This method assigns class
membership to an input pattern x rather than a particular class as in K-NN. In fuzzy K-NN the result is membership
information of x to each class. The advantage of using fuzzy set theory is that no arbitrary assignments are made. In
addition, the membership values of input pattern would provide a level of assurance to the results of classification. |
EXPERIMENTAL RESULTS |
| The proposed method has been implemented using C#.NET on a personal computer with Pentium IV 2.40 GHz, 1
GB DDR RAM. For training/testing, subsets of the COIL-100 database [14] of images are used, which contains about
7200 images in which about 100 different kinds of objects. To experiment the proposed method the 36 object classes are
selected. Some of the object classes are Bottle, Car, Can, Toy, Cup, and Tomato etc, as shown in Fig. c. The result is
about 2000 training images and 560 testing images, most of which are about 128 x 128 pixels in size. The experiments
were conducted to test the recognition accuracy of the proposed approach. The second objective was to verify the
robustness of the proposed method. A comparison of the performance this method with orthogonal moment based
Zernike and Legendre moment, also with the Back Propagation Network and Fuzzy K-Nearest Neighbor Network. |
| Following the framework of the proposed system in Fig. a. The image is preprocessed as follows. First the given
color image is converted into grey-scale image. In order to reduce the amount of computation instead of considering the
entire image, the edge detection operation is performed to obtain the edge of the image. For edge detection, in the
proposed method canny’s edge detection method is used. Once the edge is detected the image is applied an image
transformation process to invert the image. After that the resultant image is used for feature extraction process. First the
Hu’s Seven Moment invariant is computed using the (2) to (8). The dimension of the object and the center of the image
are computed as follows. In order to get the dimension of a shape, the vertical and horizontal projection for an edge
detected image was applied. First horizontal projection is performed by counting the total number of pixels of the edge
detected image in each row. The row with the maximum number of pixels was recorded. Then, beginning at this row,
upper and lower rows were sought. The first upper row with a projected value smaller than a threshold was marked as
the top of the edge of the object in the image, and the first lower row with a projected value smaller then a threshold
value was marked as the bottom boundary of the object in the image. The horizontal projection provides the height of the
object in the image. The same technique was then used on vertical projection to find the width of the object in the image.
Using the values obtained in the vertical projection and horizontal projection it is easier to find the center of the object.
Also the center of the image is obtained using moment invariant computation. Both the values are used for feature vector
formation. |
| The computed feature vector is processed to determine the eigenvalue of the image and stored in the database during
the training phase. During the testing phase, the same process is repeated and the computed eigenvalue for the test image
is compared with the eigenvalue retrieved from the database. The K-Nearest Neighbor classifier recognizes the object
and identifies the correct index; actually the test image belongs to. |
| To train the Back propagation neural network and compute the proper weights, a feature vector computed from the
set of training images are provided as input vector. The target pattern is given the object index and label for the object.
Once the network gets trained, the test image feature vector is given to the input layer. The BP neural network correctly
recognizes the image. In the same way the fuzzy k-Nearest neighbor classier is implemented with training/test images.
Using the similarity values, back propagation neural networks and k-nearest neighbor classifier then determines the class
of the new image. |
| A. Results on COIL-100 Database |
| From COIL-100 database, 36 objects are selected for training and testing The sample views of some objects are
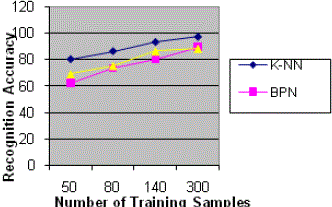
shown in Fig. b. The experiments are conducted on this database by varying the number of training samples for 97%
confidence interval. This result is shown in the Table a and Fig. c. It can be seen that the K-Nearest Neighbor algorithm
performs well when compared to the recognition rate of Back-Propagation Neural Network and Fuzzy K-Nearest
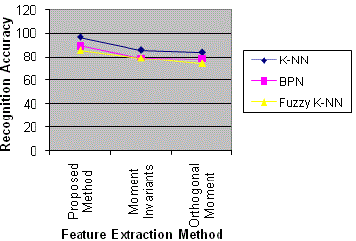
Neighbor classifier. From the Table b and Fig. d. the proposed feature extraction method moment invariants along with
the center of the object and the dimension of the object using eigenvalue provides better feature vector compared to the
other methods like orthogonal moments and moment Invariants. From the above results the proposed method of
recognizing object using eigenvalue with the help of classifier k-nearest neighbor provides effective and higher accuracy. |
CONCLUSION AND FUTURE WORK |
| In this paper it is shown that the proposed method K-Nearest Neighbor using eigenvalue computed from the local
and global features of the image, to recognize the object from an image efficiently when compared to the BPN and
Fuzzy K-Nearest Neighbors method. Also the proposed method combines the global and local features for the
construction of the feature vector. The experiments are conducted on the both the proposed method and the
conventional method. Overall, it is observed that the proposed method performing significantly better than the
conventional algorithms which use moment invariants/orthogonal moments. |
| The recognition accuracy presented here demonstrates the power of combining the global and local features using
eigenvalue. It is also expected that the proposed method may be applied to various applications like Computer enabled
vision for the partially blind, surveillance system, automated visual inspection and fish species classification. One of
the limitations of the proposed method is the recognition of single object in the given image. Our future work will
focus on using multiple object recognition. |
Tables at a glance |
 |
 |
| Table a |
Table b |
|
| |
Figures at a glance |
 |
 |
 |
 |
| Figure a |
Figure b |
Figure c |
Figure d |
|
| |
References |
- Ahmed Fawzi Otoom, Hatice Gunes, Massimo Piccardi, “Feature extraction techniques for abandoned object classification in video
surveillance,” IEEE Proceedings of the International Conference on Image processing, pp. 1368 – 1371, 2008.
- Ananthashayana V.K and Asha.V, “Appearance Based 3D Object Recognition Using IPCA-ICA,” The International Archives of the
Photogrammetry, Remote Sensing and Spatial Information Sciences. Vol. XXXVII. Part B1. Beijing, pp. 1083 – 1089, 2008.
- S. Dudani, K. Breeding, R. McGhee, “Aircraft Identification by moment Invariants,” IEEE Transactions on Computers Vol.26, No. 1, pp. 39 –
45, 1977.
- R Feraud, O Bernier, J. E. Viallet, M Collobert, “A Fast and accurate face detector based on neural networks,” IEEE Transactions on Pattern
Analysis and Machine Intelligence vol. 23, No. 1, pp. 42 -53, 2001.
- J. Gao, Z. Xie, and X. Wu, “Generic object recognition with regional statistical models and layer joint boosting,” Pattern Recognition Letters,
vol. 28, no. 16, pp. 2227-2237, 2007.
- M.K. Hu, Visual Pattern Recognition by moment Invariants, IRE Transactions on Information Theory 8, pp. 179 – 187, 1962.
- Te-Hsiu Sun, Chi-Shuan Liu, Fang-Chih Tien, “Invariant 2D Object recognition using eigenvalues of covariance matrices, re-sampling and
autocorrelation,” Expert Systems and Applications, vol.35, pp. 1966 – 1977, 2008.
- J.E. Jackson, A User’s Guide to Principal Components, John Wiley & Sons: New York, 1991.
- H. Kim, K. Nam, “Object recognition of one-DOF tools by a back propagation neural net,” IEEE Transaction on Neural Networks Vol.6, No.2,
pp. 484 – 487, 1995.
- Kun Yue, Wei-Yi Liu and Li-Ping Zhou, “ Automatic keyword extraction from documents based on multiple content-based measures”,
International Journal of Computer Systems Science and Engineering, Vol 26, No. 2, March 2011.
- LI LiLi, ZHANG YanXia and ZHAO YongHeng, “K-Nearest Neighbors for automated classification of celestial objects,” Science in China
Series G-Phys Mech Astron, Vol.51, no.7, pp. 916-922, 2008.
- Luo Juan and Oubong Gwun, “A Comparison of SIFT, PCA-SFIT and SURF,” International Journal of Image Processing, Vol.3. Issue.4., pp.
- K.Mikolajczyk and C.Schmid, “A performance evaluation of local descriptors,” IEEE Transactions on Pattern Analysis and Machine
Intelligence, vol. 27, no. 10, pp. 1615-1630, 2005.
- S.Nene, S. Nayar, H. Murase, Columbia object image library (COIL – 100): Technical report, CUCS-006-96, 1996.
- K.Ohba, K. Ikeuchi, “Detectability, uniqueness, and reliability of eigen windows for stable verification of partially occluded objects,” IEEE
Transactions on Pattern Analysis and Machine Intelligence Vol.19, No.9, pp. 1043-1048, 1997.
- Xiaowu Chen, Yongtao Ma and Qinping Zhao, “Multi-category web object extraction based on relation schema”, International Journal of
Computer Systems Science and Engineering, Vol. 25, No. 6, November 2010.
- J. Zhang, X. Zhang, H. Krim, G.G. Walter, “Object representation and recognition in shape spaces,” Pattern Recognition, Vol. 36, pp. 1143 –
1154, 2003.
- Xuan Wang, Bin Xiao, Jian-Feng Ma, and Xiu-Li Bi. “Scaling and rotation invariant analysis approach to object recognition based on Radon
and Fourier-Mellin transforms” Pattern Recogn.Vol. 40, No.12, pp.3503-3508, 2007.
- Daggu Venkateshwar Rao, Shruti Patil, Naveen Anne Babu and V Muthukumar, "Implementation and Evaluation of Image Processing
Algorithms on Reconfigurable Architecture using C-based Hardware Descriptive Languages" International Journal of Theoretical and Applied
Computer Sciences, Vol. 1 No.1, pp. 9–34, 2006.
- Muralidharan, R. and C. Chandrasekar, 3D object recognition using multiclass support vector machine-k-nearest neighbor supported by local
and global feature. Journal of Computer Scince, Vol.8, No.8, pp.1380-1388, 2012.
|