ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| M. Kavitha1, CH. Rajendra Prasad2, Dr. Syed Musthak Ahmed3 Department of ECE, SR Engineering College, Warangal, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
This paper proposed the design of high speed Vedic Multiplier using the techniques of Ancient Indian Vedic Mathematics that have been modified to improve performance. Vedic Mathematics is the ancient system of mathematics which has a unique technique of calculations based on 16 Sutras. The work has proved the efficiency of Urdhva Triyagbhyam– Vedic method for multiplication which strikes a difference in the actual process of multiplication itself. It enables parallel generation of intermediate products, eliminates unwanted multiplication steps with zeros and scaled to higher bit levels using Karatsuba algorithm with the compatibility to different data types. Urdhva tiryakbhyam Sutra is most efficient Sutra (Algorithm), giving minimum delay for multiplication of all types of numbers, either small or large. Further, the Verilog HDL coding of Urdhva tiryakbhyam Sutra for 32x32 bits multiplication and their FPGA implementation by Xilinx Synthesis Tool on Spartan 3E kit have been done and output has been displayed on LCD of Spartan 3E kit. The synthesis results show that the computation time for calculating the product of 32x32 bits is 31.526 ns.
Keywords |
| Vedic mathematics, urdhva triyakbhyam sutra, karatsuba - ofman algorithm. |
INTRODUCTION |
| Multiplication is an important fundamental function in arithmetic operations. Multiplication-based operations such as Multiply and Accumulate(MAC) and inner product are among some of the frequently used Computation- Intensive Arithmetic Functions(CIAF) currently implemented in many Digital Signal Processing (DSP) applications such as convolution, Fast Fourier Transform(FFT), filtering and in microprocessors in its arithmetic and logic unit [1]. Since multiplication dominates the execution time of most DSP algorithms, so there is a need of high speed multiplier. Currently, multiplication time is still the dominant factor in determining the instruction cycle time of a DSP chip. The demand for high speed processing has been increasing as a result of expanding computer and signal processing applications. Higher throughput arithmetic operations are important to achieve the desired performance in many realtime signal and image processing applications [2]. One of the key arithmetic operations in such applications is multiplication and the development of fast multiplier circuit has been a subject of interest over decades. Reducing the time delay and power consumption are very essential requirements for many applications [2, 3]. This work presents different multiplier architectures. Multiplier based on Vedic Mathematics is one of the fast and low power multiplier. Minimizing power consumption for digital systems involves optimization at all levels of the design. This optimization includes the technology used to implement the digital circuits, the circuit style and topology, the architecture for implementing the circuits and at the highest level the algorithms that are being implemented. Digital multipliers are the most commonly used components in any digital circuit design. They are fast, reliable and efficient components that are utilized to implement any operation. Depending upon the arrangement of the components, there are different types of multipliers available. Particular multiplier architecture is chosen based on the application. In many DSP algorithms, the multiplier lies in the critical delay path and ultimately determines the performance of algorithm. The speed of multiplication operation is of great importance in DSP as well as in general processor. In the past multiplication was implemented generally with a sequence of addition, subtraction and shift operations. There have been many algorithms proposals in literature to perform multiplication, each offering different advantages and having tradeoff in terms of speed, circuit complexity, area and power consumption. |
| The multiplier is a fairly large block of a computing system. The amount of circuitry involved is directly proportional to the square of its resolution i.e. A multiplier of size n bits has n2 gates. For multiplication algorithms performed in DSP applications latency and throughput are the two major concerns from delay perspective. Latency is the real delay of computing a function, a measure of how long the inputs to a device are stable is the final result available on outputs. Throughput is the measure of how many multiplications can be performed in a given period of time; multiplier is not only a high delay block but also a major source of power dissipation. That’s why if one also aims to minimize power consumption, it is of great interest to reduce the delay by using various delay optimizations. |
| Digital multipliers are the core components of all the digital signal processors (DSPs) and the speed of the DSP is largely determined by the speed of its multipliers[11]. Two most common multiplication algorithms followed in the digital hardware are array multiplication algorithm and Booth multiplication algorithm. The computation time taken by the array multiplier is comparatively less because the partial products are calculated independently in parallel. The delay associated with the array multiplier is the time taken by the signals to propagate through the gates that form the multiplication array. Booth multiplication is another important multiplication algorithm. Large booth arrays are required for high speed multiplication and exponential operations which in turn require large partial sum and partial carry registers. Multiplication of two n-bit operands using a radix-4 booth recording multiplier requires approximately n / (2m) clock cycles to generate the least significant half of the final product, where m is the number of Booth recorder adder stages. Thus, a large propagation delay is associated with this case. Due to the importance of digital multipliers in DSP, it has always been an active area of research and a number of interesting multiplication algorithms have been reported in the literature [4]. |
| In this, Urdhva tiryakbhyam Sutra is first applied to the binary number system and is used to develop digital multiplier architecture. This is shown to be very similar to the popular array multiplier architecture. This Sutra also shows the effectiveness of to reduce the NXN multiplier structure into an efficient 4X4 multiplier structures. Nikhilam Sutra is then discussed and is shown to be much more efficient in the multiplication of large numbers as it reduces the multiplication of two large numbers to that of two smaller ones. The proposed multiplication algorithm is then illustrated to show its computational efficiency by taking an example of reducing a 4X4-bit multiplication to a single 2X2-bit multiplication operation [4]. This work presents a systematic design methodology for fast and area efficient digit multiplier based on Vedic mathematics .The Multiplier Architecture is based on the Vertical and Crosswise algorithm of ancient Indian Vedic Mathematics [5]. |
VEDIC MATHEMATICS |
| Vedic mathematics is part of four Vedas (books of wisdom). It is part of Sthapatya- Veda (book on civil engineering and architecture), which is an upa-veda (supplement) of Atharva Veda. It gives explanation of several mathematical terms including arithmetic, geometry (plane, co-ordinate), trigonometry, quadratic equations, factorization and even calculus. |
| His Holiness Jagadguru Shankaracharya Bharati Krishna Teerthaji Maharaja (1884- 1960) comprised all this work together and gave its mathematical explanation while discussing it for various applications. Swamiji constructed 16 sutras (formulae) and 16 Upa sutras (sub formulae) after extensive research in Atharva Veda. Obviously these formulae are not to be found in present text of Atharva Veda because these formulae were constructed by Swamiji himself. Vedic mathematics is not only a mathematical wonder but also it is logical. That’s why it has such a degree of eminence which cannot be disapproved. Due these phenomenal characteristics, Vedic maths has already crossed the boundaries of India and has become an interesting topic of research abroad. Vedic maths deals with several basic as well as complex mathematical operations. Especially, methods of basic arithmetic are extremely simple and powerful [2, 3]. |
| The word “Vedic” is derived from the word “Veda” which means the store-house of all knowledge. Vedic mathematics is mainly based on 16 Sutras (or aphorisms) dealing with various branches of mathematics like arithmetic, algebra, geometry etc[15]. These Sutras along with their brief meanings are enlisted below alphabetically. |
| 1. (Anurupye) Shunyamanyat – If one is in ratio, the other is zero. |
| 2. Chalana-Kalanabyham – Differences and Similarities. |
| 3. Ekadhikina Purvena – By one more than the previous One. |
| 4. Ekanyunena Purvena – By one less than the previous one. |
| 5. Gunakasamuchyah – The factors of the sum is equal to the sum of the factors. |
| 6. Gunitasamuchyah – The product of the sum is equal to the sum of the product. |
| 7. Nikhilam Navatashcaramam Dashatah – All from 9 and last from 10. |
| 8. Paraavartya Yojayet – Transpose and adjust. |
| 9. Puranapuranabyham – By the completion or non completion. |
| 10. Sankalana- vyavakalanabhyam – By addition and by subtraction. |
| 11. Shesanyankena Charamena – The remainders by the last digit. |
| 12. Shunyam Saamyasamuccaye – When the sum is the same that sum is zero. |
| 13. Sopaantyadvayamantyam – The ultimate and twice the penultimate. |
| 14. Urdhva-tiryagbhyam – Vertically and crosswise. |
| 15. Vyashtisamanstih – Part and Whole. |
| 16. Yaavadunam – Whatever the extent of its deficiency. |
| These methods and ideas can be directly applied to trigonometry, plain and spherical geometry, conics, calculus (both differential and integral), and applied mathematics of various kinds. As mentioned earlier, all these Sutras were reconstructed from ancient Vedic texts early in the last century. Many Sub-sutras were also discovered at the same time, which are not discussed here. The beauty of Vedic mathematics lies in the fact that it reduces the otherwise cumbersome-looking calculations in conventional mathematics to a very simple one. This is so because the Vedic formulae are claimed to be based on the natural principles on which the human mind works. This is a very interesting field and presents some effective algorithms which can be applied to various branches of engineering such as computing and digital signal processing [ 1,4]. |
| The multiplier architecture can be generally classified into three categories. First is the serial multiplier which emphasizes on hardware and minimum amount of chip area. Second is parallel multiplier (array and tree) which carries out high speed mathematical operations. But the drawback is the relatively larger chip area consumption. Third is serial- parallel multiplier which serves as a good trade-off between the times consuming serial multiplier and the area consuming parallel multipliers. |
DESIGN OF VEDIC MULTIPLIER |
| A. Urdhva – Triyagbhyam(Vertically and Crosswise): |
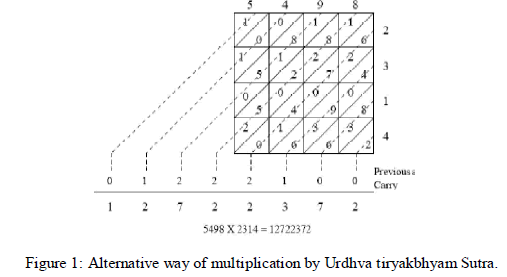
| Urdhva tiryakbhyam Sutra is a general multiplication formula applicable to all cases of multiplication. It literally means “Vertically and Crosswise”. To illustrate this multiplication scheme, let us consider the multiplication of two decimal numbers (5498 × 2314). The conventional methods already know to us will require 16 multiplications and 15 additions. |
| An alternative method of multiplication using Urdhva tiryakbhyam Sutra is shown in Fig. 1. The numbers to be multiplied are written on two consecutive sides of the square as shown in the figure. The square is divided into rows and columns where each row/column corresponds to one of the digit of either a multiplier or a multiplicand. Thus, each digit of the multiplier has a small box common to a digit of the multiplicand. These small boxes are partitioned into two halves by the crosswise lines. Each digit of the multiplier is then independently multiplied with every digit of the multiplicand and the two-digit product is written in the common box. All the digits lying on a crosswise dotted line are added to the previous carry. The least significant digit of the obtained number acts as the result digit and the rest as the carry for the next step. Carry for the first step (i.e., the dotted line on the extreme right side) is taken to be zero [9]. |
 |
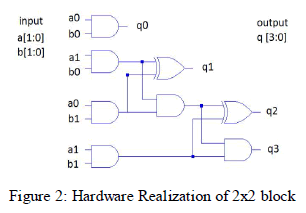
| The design starts first with Multiplier design, that is 2x2 bit multiplier as shown in figure 2. Here, “Urdhva Tiryakbhyam Sutra” or “Vertically and Crosswise Algorithm”[4] for multiplication has been effectively used to develop digital multiplier architecture. This algorithm is quite different from the traditional method of multiplication, which is to add and shift the partial products. |
 |
| To scale the multiplier further, Karatsuba – Ofman algorithm can be employed [6]. Karatsuba-Ofman algorithm is considered as one of the fastest ways to multiply long integers. It is based on the divide and conquer strategy [11]. A multiplication of 2n digit integer is reduced to two n digit multiplications, one (n+1) digit multiplication, two n digit subtractions, two left shift operations, two n digit additions and two 2n digit additions. |
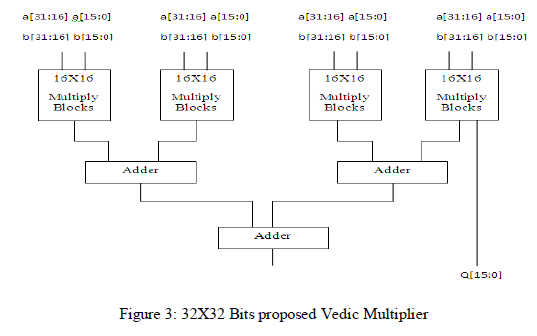
| For Multiplier, first the basic blocks, that are the 2x2 bit multipliers have been made and then, using these blocks, 4x4 block has been made by adding the partial products using carry save adders and then using this 4x4 block, 8x8 bit block, 16x16 bit block and then finally 32 x 32 bit Multiplier as shown in figure 3 has been made [7]. |
 |
IMPLEMENTATION OF VEDIC MULTIPLIER |
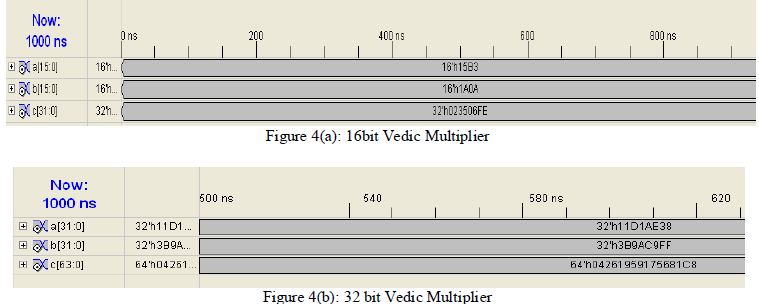
| The proposed multiplications were implemented using two different coding techniques viz., conventional shift & add and Vedic technique for 4, 8, 16, and 32 bit multipliers. It is evident that there is a considerable increase in speed of the Vedic architecture. The simulation results for 16, and 32 bit multipliers are shown in the figures 4.(a), (b), (c) respectively. |
Simulation Results: |
 |
 |
| The worst case propagation delay in the Optimized Vedic multiplier case was found to be 31.526ns. To compare it with other implementations the design was synthesized on XILINX: SPARTAN: xc3s500e-5fg320 [17]. Figure 1 shows the synthesis result for various implementations. The result obtained from proposed Vedic multiplier is faster than Karatsuba Algorithm. |
CONCLUSION |
| The designs of 32x32 bits Vedic multiplier have been implemented on Spartan XC3S500-5-FG320. The design is based on Vedic method of multiplication [3]. The worst case propagation delay in the Optimized Vedic multiplier case is 31.526ns. It is therefore seen that the Vedic multipliers are much faster than the conventional multipliers. This gives us method for hierarchical multiplier design. So the design complexity gets reduced for inputs of large no of bits and modularity gets increased. Urdhva tiryakbhyam, Nikhilam and Anurupye sutras are such algorithms which can reduce the delay, power and hardware requirements for multiplication of numbers. FPGA implementation of this multiplier shows that hardware realization of the Vedic mathematics algorithms is easily possible. The high speed multiplier algorithm exhibits improved efficiency in terms of speed. |
References |
|