Abdelmalek M*
High School of Management, Aboubekr Belkaid University, Tlemcen, Algeria
Received Date: 02/03/2017; Accepted Date: 17/03/2017; Published Date: 22/03/2017
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In this article, we derive a flux formula in a weighted manifold, using the weighted Newton transformations and introducing the notion of weighted higher order mean curvature, this formula generalizes. Reilly’s original formula and the flux formula obtained by Alias, Lopez and Malcarne [1]. In particular, we obtain a similar balancing formula obtained by Rosenberg. Finally, we give some special cases of our formula.
Weighted manifolds, Weighted, Newton transformation, rth mean curvature, Weighted mean curvature
Most of the useful integral formulas in Riemannian geometry are obtain by computing the divergence of certain vector fields and then apply the divergence theorem. In the authors gave a flux formula. In particular, they derive a similar balancing formula given by Rosenberg [2]. As an application to this flux formula they gave an estimation of the higher order mean curvature Hr of a hypersurface in space forms by the geometry of its boundary [1]. Motivated by the work of these authors, we give in this work a flux formula in the case of weighted manifolds. Recall that a weighted manifold (called also a manifold with density) is a Riemannian manifold M endowed with a smooth positive density e-f with respect to the Riemannian measure. We proof the following proposition.
Proposition 1
Let 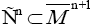 an oriented connexion sub-manifold of
an oriented connexion sub-manifold of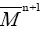 and
and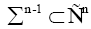 a compact hyper-surface of Pn .
a compact hyper-surface of Pn .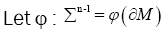 a compact oriented hyper-surface of boundary
a compact oriented hyper-surface of boundary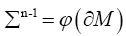 Denoting by N the global vector fields normal to Mn, and ν the outpointing vector normal to
Denoting by N the global vector fields normal to Mn, and ν the outpointing vector normal to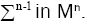 Then for 1 ≤ k ≤ n and for every conformal vector field
Then for 1 ≤ k ≤ n and for every conformal vector field 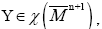 we have
we have
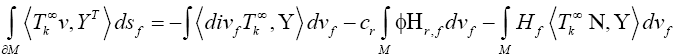
Where 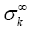 is the weighted Newton transformations, and Hr,f is the weighted higher order mean curvature.
is the weighted Newton transformations, and Hr,f is the weighted higher order mean curvature.
As a consequence of this proposition, we obtain some special cases. In particular, we obtain a balancing formula for 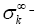 minimal hyper-surface in space forms. The paper is organized as follows. Section 2 provides some preliminaries. The main results of the paper are contained in Section 3. Throughout the paper everything (manifolds, metrics, etc.) is assumed to be C∞ -differentiable and oriented [3-5].
minimal hyper-surface in space forms. The paper is organized as follows. Section 2 provides some preliminaries. The main results of the paper are contained in Section 3. Throughout the paper everything (manifolds, metrics, etc.) is assumed to be C∞ -differentiable and oriented [3-5].
Preliminaries
In this section we introduce the basic notations used in the paper. we will recall some definitions and properties of the weighted symmetric functions and the weighted Newton transformations. For more details see [3],[7].
Let  be a
be a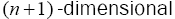 Riemannian manifold. Let
Riemannian manifold. Let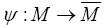 be an isometrically immersed hypersurface. Denoting by
be an isometrically immersed hypersurface. Denoting by 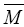 and
and 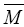 the Levi civita connections of
the Levi civita connections of 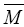 and
and 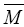 respectively. Then, the Weingarten formulae of the hypersurface is written as
respectively. Then, the Weingarten formulae of the hypersurface is written as
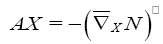
Where Τ is the shape operator of the hypersurface M with respect to the Guass map N, and Τ denotes the orthogonal projection on the vector bundle tangent to M,
It is well know that A is a linear self adjoint operator. At each point p∈M, its eigenvalues μ1,..., μn are the principales curvatures of M [6,7].
Associate to the shape operator A , define the weighted elementary symmetric fucntions 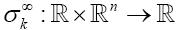 recursively by:
recursively by:
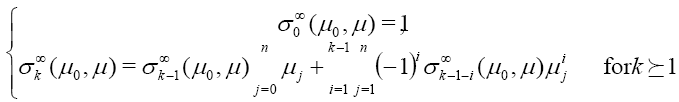
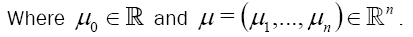
In particular 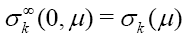 is nothing but the classical elementary symmetric functions define in [8].
is nothing but the classical elementary symmetric functions define in [8].
Definition
The weighted Newton transformations (W.N.T) 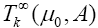 are define inductively form A by
are define inductively form A by
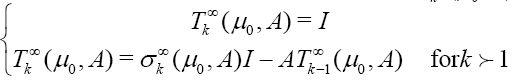
Where 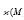 denote the identity of
denote the identity of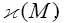
Or equivalentely by 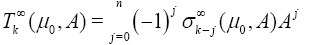
Where 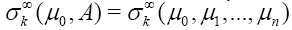 and n μ ,...,μ 1 are the eigenvalues of
and n μ ,...,μ 1 are the eigenvalues of 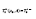
We denote to simplify 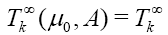 and
and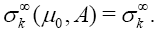
In particular 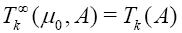 is the classical Newton transformations introduced in [8]
is the classical Newton transformations introduced in [8]
These two quantities has the same proprietes of the classical symmetric functions and Newton transformations [3].
Proposition 2
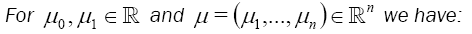
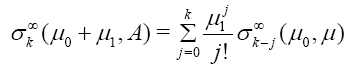
In particular 1, 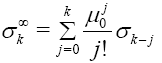
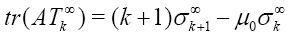
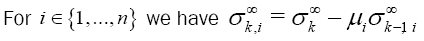
And the 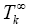 eigenvalue of
eigenvalue of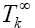 is equal to
is equal to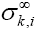
Where 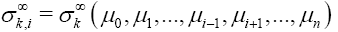
Definition 1: The weighted rth mean curvature Hr,f is given by:
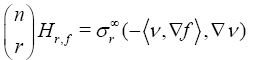
Where ν is the outpointing vectors field normal to M in
In particular for r =1, we have 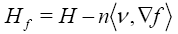
Is the weighted mean curvature of the hypersurface M
Definition 2: We say that an hypersurface M of 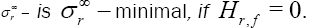
In particular; M is f −minimal, if Hf= 0 . Or equivalentely 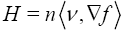
Definition 3: The weighted divergence of the weighted Newton transformations is define by:
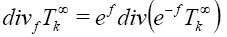
Where
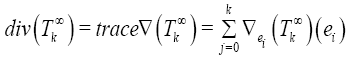
And {e1,…,en} is an orthonormale basis of the tangent space of M.
In particular, if f vanish identiqualy and μ=0, then we obtain the classical difinition of the divergence of the Newton tranformations.
I found here some isoperimetrics inequalities. Now I am trying to find a variational formula for the wighted higher order mean curvature [9].
In conclusion, my steps are:
1. Calculate the divergence 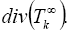 (The fact that we calculate this quantity is to use it in the two last steps by using the divergence theorem for the weighte Newton transformation).
(The fact that we calculate this quantity is to use it in the two last steps by using the divergence theorem for the weighte Newton transformation).
2. Compare 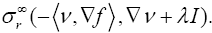
3. Find variation (critical point) for 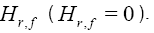
4. Minimise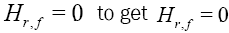
Forn the two first points, I found the way.
I think the two last ones are equivalent to the study of the variation 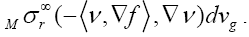
If you have an idea about how we study the two last points, because if we can find such
realtion, this result gives a geometric interpretation of our quantity ( H r,f ).