International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A Novel Blend of DWT and SVD for Medical Images Using Digital Watermarking

Mamtha H K1 and Dr Sujatha B K2
  1. Assistant Processor, Department of ECE, M S Ramaiah Institute of Technology, Bangalore, Karnataka, India
  2. Professor, Department of TCE, M S Ramaiah Institute of Technology, Bangalore, Karnataka, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

A reliable medical image management must ensure proper safeguarding of the medical images while maintaining high dependability. Safeguarding the medical information of the patients is a major concern in all hospitals Also one should be able to verify that information belongs to the correct patient and is issued from the right source. Digital watermarking is a technique popularly used to protect the confidentiality of medical information particularly images. In this paper we propose a novel blend of Digital Wavelet Transform (DWT) and Singular Value Decomposition (SVD) for watermarking the medical images. SVD is applied to the approximate and vertical coefficients of the wavelet transform in order to improve medical image protection in terms of peak signal to noise ratio(PSNR), Mean Square Error(MSE) and Normalized Cross-correlation(NC) between original and watermarked images.

Keywords
Discrete Wavelet Transform, Singular Value Decomposition, Watermarking, Peak signal to noise ratio,Mean Square Error, Normalized Cross Correlation

INTRODUCTION
The evolution of medical information systems has been supported by advances in information technology. Easier access to internet has evolved into new challenges regarding security of sensitive medical information [3,6]. DWT has been widely used in many fields, including image processing.The high spreading of broadband networks and new developments in digital technology has made ownership protection and authentication of digital data since it makes possible to identify the author of an image by embedding secret information to the host image. Robust watermarks are designed to resist any modifications and are designed for the copyright protection. Frequency (transform) domain methods are based on using some invertible transformations like discrete cosine transform (DCT), discrete Fourier transform (DFT), discrete wavelet transform (DWT). Watermarking is a robust method for hiding information on multimedia files. Digital watermarking is a process to embed some information called watermark into different kinds of media called Cover Work. It is used to protect the copyrights and restores the ownership. In spatial domain techniques, the watermark is applied in the pixel domain.[4]. In Frequency domain the watermark is embedded into transformed coefficients of image giving more robust images against watermarking attacks [2]Digital watermark is a perceptually invisible pattern embedded in a digital image. The watermark can carry information about the owner of the image or the recipient the image itself or some additional information with the image (image caption embedding). Typically, watermarking the original image is needed for watermark extraction techniques. In oblivious techniques, the watermark can be extracted from the watermarked or attacked image without access to the original image.

LITERATURE SURVEY
Giakoumi et al have proposed a health data management system using wavelet- based multiple watermarking scheme.The robustness of the method is enhanced through a form of hybrid coding, which includes repetitive embedding of watermarks. Multiple other studies have demonstrated the effectiveness of wavelets in watermarking[4, 7 ]. Use of SVD is shown to give resilience to attacks such as signal processing operations (such as lossy compression, filtering etc) and common geometric transformations (such as cropping, scaling, translation and rotation etc) [5, 9]. A reliable watermark extraction scheme is developed for the extraction of watermark from distorted image. Modification in all frequencies allows the development of a watermarking scheme that is robust to a wide range of attacks[8].
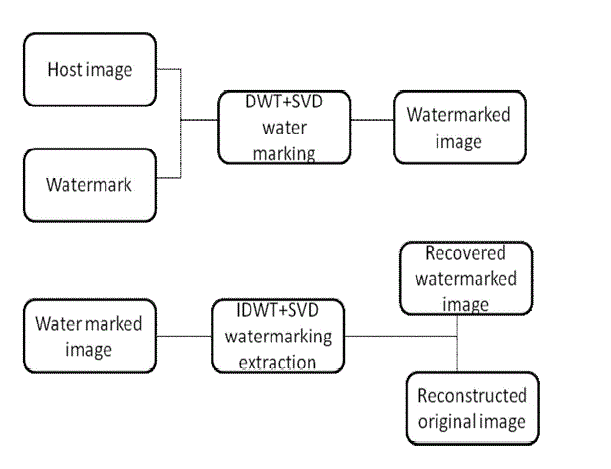
In this study we have considered medical images of three popular categories namely Computed Tomography (CT), Magnetic Resonance Image (MRI) [1] and Positron Emission Tomography(PET). An optimal watermarking technique based on SVD and DWT domain for grey-scale images is evolved based on the performance parameters namely peak signal to noise ratio(PSNR), Mean Square Error(MSE) and Normalized Cross-correlation(NC) . The algorithm embeds the watermark by modifying the singular values of the host image with multiple scaling factors.
Paper is organized as follows: Section 3 discusses about the proposed methodology. Section 4 deals with the algorithms for watermarking and extraction as well as the performance parameters considered. A discussion of the experimental results is done in Section 5. Section 6 discusses the conclusion and the future work.

PROPOSED METHODOLOGY
The medical images considered are CT, MRI and PET images. Initially the watermark is embedded in the image by setting an initial value of scaling factor α. The original image is reconstructed by extraction of the watermark. Optimum value of scaling factor is found by iteration of the above and tabulating the results to obtain desirable values of PSNR, MSE and NC.
Embedding of a watermark is made by modifications of the transform coefficients, accordingly to the watermark or its spectrum. The inverse transform is applied to obtain the marked image. The image is decomposed into four sub-bands namely LL,LH,HL,HH.
Watermarking is being done by embedding the watermark in the first and second level DWT sub-bands of the host image, followed by the application on the selected DWT sub bands. A hybrid DWT-SVD-based watermarking scheme is developed that requires less computation effort yielding better performance. A sequence Haar wavelet is of rescaled "square-shaped" functions which together form a wavelet family or basis.
The Haar wavelet's mother wavelet function á´ª(t) can be described as
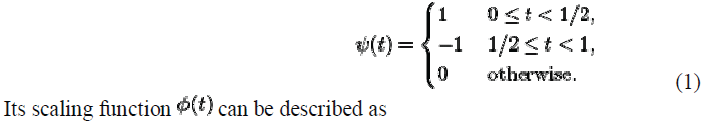equation
equation
Singular Value Decomposition (SVD)
Singular Value Decomposition is a matrix factorization technique having many applications in image processing. SVD is based on a theorem from linear algebra which says that a rectangular matrix A can be broken down into the product of three matrices - an orthogonal matrix U, a diagonal matrix S, and the transpose of an orthogonal matrix V . The theorem is presented as:
A = USVT where UTU = I, VTV = I; the columns of U are orthonormal eigenvectors of AAT , the columns of V are orthonormal eigenvectors of ATA, and S is a diagonal matrix containing the square roots of eigen values from U or V in descending order.
An illustration:
equation
The diagonal elements in S are the singular values of A.
The SVD of an image is computed to obtain two orthogonal matrices U, V and a diagonal matrix the watermark W is added to the matrix S. Then, a new SVD process is performed on the new matrix S+kW to get Uw, Sw and Vw, where k is the scale factor that controls the strength of the watermark embedded to the original image. Then, the watermarked image Fw is obtained by multiplying the matrices U, Sw, and V T . The steps of watermark embedding are summarized as follows:
equation

PROPOSED ALGORITHM
The medical images considered are CT, MRI and PET images. Initially the watermark is embedded in the image by setting an initial value of scaling factor α. The original image is reconstructed by extraction of the watermark. Optimum value of scaling factor is found by iteration of the above and tabulating the results to obtain desirable values of PSNR, MSE and NC.

Algorithm to embed watermark into cover image:
1)Read the cover image & watermark image.
2)Apply DWT to cover image to obtain approximation, horizontal, vertical, diagonal DWT coefficients i.e. ca1, ch1, cv1, cd1 (LL, HL, LH, HH)
3)Calculate the approximate DWT coefficient by adding the watermark image as in equation Ca1 (i,j)=ca1(i,j)+(α*watermark) (14)
Where Ca1 & ca1 are the modified & original approximation coefficients and α is a scaling value as set to10.
4)Apply SVD to the decomposed sub-bands(LL)
5)Find Inverse DWT
6)Increment α, apply SVD and inverse DWT.

Algorithm for Watermark Extraction:
1) Apply two‐dimensional DWT, to obtain the first level decomposition of the watermarked cover image i.e. c1a1, c1h1, c1v1, c1d1
2) Extract the watermark from vertical & approximation DWT coefficient as per the equation WN= (SN-S)/ α; where α=10
3)Apply two‐dimensional DWT, to obtain the first level decomposition of the watermarked image. LL1, HL1, LH1, HH1.

Performance parameters:
The peak signal-to-noise ratio (PSNR) is used to measure the quality of reconstructed images. PSNR is the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. Because many signals have a very wide dynamic range, PSNR is usually expressed in terms of the logarithmic decibel scale. PSNR is most easily defined via the mean square error (MSE). Given a noisefree m×n monochrome image I and its noisy approximation K
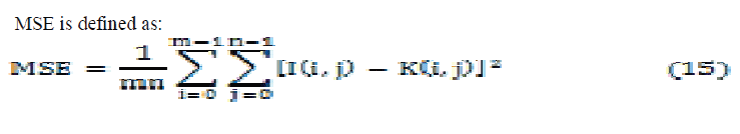equation
equation
Where f* denotes the complex conjugates of ‘f’ and’á´¦’ is the time lag.

RESULTS
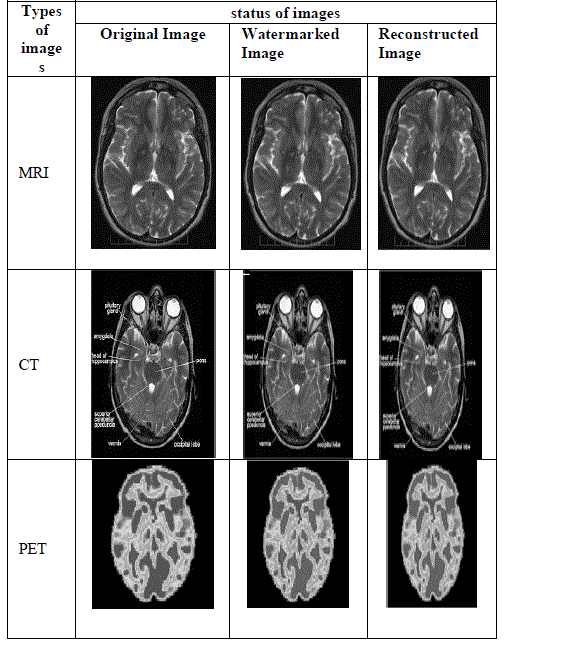
Fig 2. shows the sample original, watermarked and reconstructed images of the 3 categories of medical images considered. Then peak signal to noise ratio(PSNR), mean square error(MSE), and normalized cross-correlation (NC) of the extracted image are calculated.
Then peak signal to noise ratio(PSNR), mean square error(MSE), and normalized cross-correlation (NC) of the extracted image for MRI image is shown in Table 1 peak signal to noise ratio(PSNR), mean square error(MSE), and normalized cross-correlation (NC) of the extracted image for CT images is shown in Table 2 and Table 3 shows the PSNR,MSE and NC for PET images.
The proposed work has been implemented using Matlab R2013a.The medical images considered are MRI, CT and PET obtained from the database “MRI Images”. The images have been watermarked using a text message. The extraction is done by decomposing the original image using Haar wavelets and embedding the SVD coefficients in the Approximate and Vertical components of the decomposed image. Fig 2 shows the sample original, watermarked and reconstructed images of the 3 categories of medical images considered. Then peak signal to noise ratio(PSNR), mean square error(MSE), and normalized cross-correlation (NC) of the extracted image are calculated and tabulated as shown in Tables 1, 2 and 3. On experimentation the scaling factors below 8 and above 14 were found to give unrealistic PSNR values of 0 or infinity. Hence the scaling factor range is fixed in the range of 8 to 14. From Tables 1, 2 and 3, it can be observed that PSNR values are in the range of 62 to 80 dB while the MSE is in the range of 0.0015 to 0.048. With increasing values of scaling factor the PSNR is seen to reduce while MSE if found to increase as shown in the tables1,2,and 3.From the tabulation, optimum value for scaling factor is noted to be 10 which gives an average PSNR of 70 dB and MSE of 0.006. The results shows a good combination of PSNR(above 70dB) and MSE(below 0.0055). This justifies our selection of optimum scaling factor.

CONCLUSION AND FUTURE WORK
The watermarking can be used to provide proof of the authenticity of medical images that is to say that the medical information of one patient has been issued from the right source.the watermark has been inserted with out interfering with the documents usefulness.The proposed methodology uses DWT +SVD techniques to calculate PSNR and MSE for different medical images .SVD is very aptly used with DWT. It has been tested for different images and PSNR,MSE,NC are calculated for each image.
This work contributes in utilizing SVD generous properties that are unexploited in image processing. This paper also introduces new trends and challenges in using SVD in image processing applications.. This paper opens many tracks for future work in using SVD as an imperative tool in signal processing.

Tables at a glance
Table icon Table icon Table icon
Table 1 Table 2 Table 3

Figures at a glance
Figure Figure
Figure 1 Figure 2

References