Keywords
|
| Fractional Order Digital Differentiator (FODD), fractional order derivative, least square method, fractional calculus. |
INTRODUCTION
|
| Fractional calculus is a 300 year old topic and a lot of work has been done in the area of fractional calculus. For past three centuries, this subject was studied by several mathematicians and only in last few years, this has been utilized in several applied fields of engineering, science and economics. However recent attempt is on to have definition of fractional derivative as local operator specifically to fractal science theory. In the recent years, fractional calculus received great attention in many engineering fields. Fractional order digital differentiator is an important topic in the area of fractional calculus, because it computes fractional derivative of the digital signal without known function. The main reason of interest in this field is that there are some systems present in nature whose response can be accurately studied with the help of fractional derivative. Fractional order basically signifies us that order of system is a non-integer, for the derivative of a function can be written as |
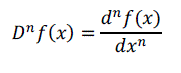 |
| If the value of n is anon- integer.n=1/2 is we can write derivative of as |
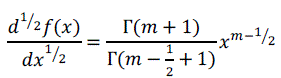 |
| so, by using gamma function, we can calculate the fractional order derivative of a function with integer order. In the field of fractional calculus several methods have been implemented for the calculation of fractional order derivative of the signal. |
| In this paper, we have visualized the method of Savitzky-Golay to enhance the performance of the signal which is contaminated with noise. Various other methods are also proposed for the efficient smoothening of the signal and to calculate its fractional order derivative. But these differentiators are not appropriate to compute the fractional order derivative of the contaminated signal, genetic algorithm method is also used but it is not efficient because of its large computation. Savitzky-Golay filter is a regression technique, which can estimate the integer order derivative of contaminated signal but not for fractional order. In order to overcome this problem, Fractional Order Savitzky-Golay Differentiator (FOSGDD) with the help of least square method and Riemann-Liouville technique is proposed, which can estimate the fractional order derivative of the contaminated signal. Further in this paper we have applied different signals to verify the proposed work. Computation time is also calculated to specify the efficiency of the method. |
| We have applied chirp signal to this differentiator because chirp signal and fractional order differentiator can be efficiently used in the area of radar and sonar. Chirp signals are mostly observed in the sonar and radar. Chirp signals are interchangeably used with sweep signal. It has other applications also such as spread spectrum communication, so there are enormous uses of applying chirp signal to fractional differentiator. |
RELATED WORK
|
| We studied the definition and properties of S-G (Savitzky-Golay)filters and presented how they can be designed easily using polynomial approximation of an impulse sequence. In contrast to most considerations of S-G filters, weconcentrated on the frequency domain properties, and offered an approximate formula for the 3-dB cutoff frequency as a function of polynomialorder ?? and impulse response half-length ??. Engineers with a frequency domain mindset may find this useful if they choose to use S-G filters in their application [6]. SG filter is used to implement fractional order differentiator and the efficiency of this method is validated. Proposed method is compared with several popular methods and it is analyzed that the proposed method is better than all the other methods[4].The fractional derivative of power function is defined. Then, the impulseresponse of fractional order differentiator is obtained by solving linear equations of Vandermonde form. Finally, one example is used to demonstrate that the fractional derivatives of digital signals are easily computed by using proposed filtering technique. This paper proposes easy recursive formulas to design fractional order differentiators with low error as compared to previous methods [5]. |
DESIGN METHOD
|
| We want to smooth the given uniformly sampled signal and to estimate its order derivative using a filtering window of size , for the , is a no so that we can compute least square polynomial. |
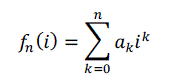 |
| where is a polynomial function with degree is the coefficient to fit the given signal. If we want to accurately calculate the coefficient , least square method will be used, for better implementation (3) can be written in matrix form as |
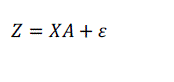 |
| where denotes the measured signal points in the filtering window, implies coefficient vector of polynomial function, is the estimation error and is a × + 1) Vander-monde matrix, written as |
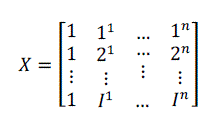 |
| We can obtain the coefficients of best fit polynomial by minimizing the sum of squared errors between the actual data and fitting points, hence we can obtain |
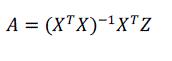 |
| Using (6) we will get estimation of the given signal by |
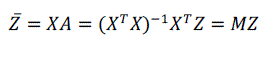 |
| Where denotes the moving window coefficient matrix, which we will use for the smoothening of the given signal. If we want to smooth the value of the signal, we will use coefficient of to implement. Integer order derivative of (3) can be given as |
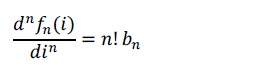 |
| Hence, the order derivative of the given signal can be estimated by |
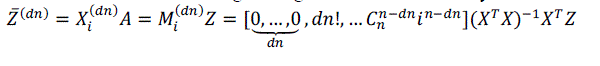 |
| Here, denotes the order derivative of the point , denotes the coefficient of the derivative and denotes the moving window’s coefficients. When is equal to zero, (9) is equivalent to (7) and can be used for the smoothening of the given signal |
| Further in this paper, Riemann-Liouville definition is used for the purpose of generalization of Savitzky-Golay differentiator from integer order to fractional order. |
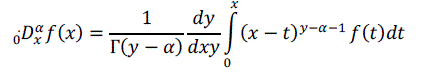 |
| where 0 is the Gamma Function. Assuming the signal , then the above equation becomes. |
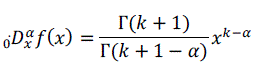 |
| If a is integer, then the fractional order differentiation is equivalent to integer order. In the proposed method, operation is linear and the rule of linearity follows. Using these properties final result can be written as |
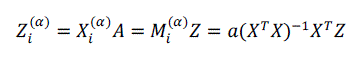 |
| Where a is given by |
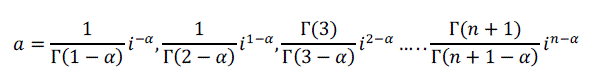 |
| as we have observed from the previous equations that matrix is the key to affect the computation time. We will face problems in computation, if is too large, so to efficiently overcome this problem, we will increase the sampling interval of the observed signal. |
SIMULATION& RESULTS
|
| A.In this section accuracy of the proposed algorithm will be validated. First we will compute the coefficients for the moving window’s weights of the point for given and sampling interval = 1. The results are given in Table.1 for the given signal . For the verification of given results in the function using , if = 5 we can write which is same as result shown in last column of Table.1. |
| B.In this section we will compute moving window coefficient for different values of , and 1, the results are shown in Table.2 From the results it is verified that this method is efficient for the calculation of fractional order derivative of signal. The results presented in Table.2 are same as result calculated by (11). |
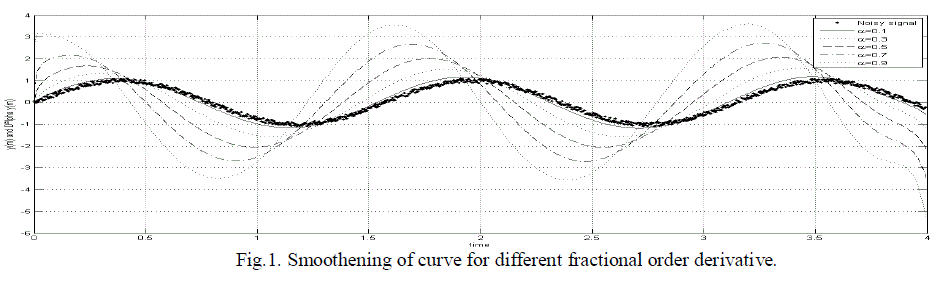
| C. In this section we will use the proposed differentiator for the purpose of smoothening of given signal sin contaminated with uniformly distributed random noise. We will take , and is changing from 0.1 to 0.9 at an interval of 0.2 result of smoothen signal is shown in Fig.1. Solid curve denotes the contaminated signal and others show the result of different values. From the result it is verified that proposed differentiator has good smoothening performance for the contaminated signal. |
| D.In this section we will apply chirp signal to the proposed differentiator, applied signal can be written as |
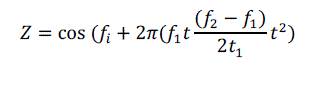 |
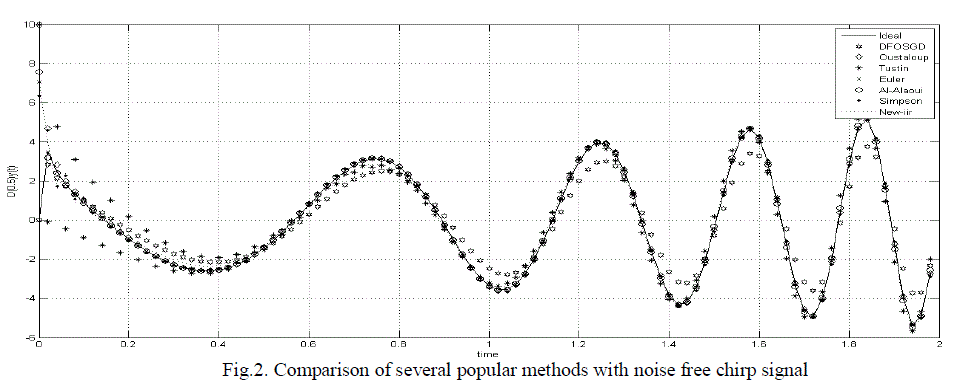
| Here, we will compare, performance of the purposed differentiator with several popular methods, such as Tustin’s method, Oustaloup’s method, Euler method, Al-Alaoui Method, Simpson’s method and a New IIR method, where the order of differentiation is taken 0.5,k = 200, n= 9. Fig.2 shows the comparison of different methods. |
| In the Fig.2 the curve is in plane line is ideal curve and the curve is in asterisk is of proposed method and the rest are of different methods, from the figure it is clear that the performance of FOSGDD is better than other methods and the RMS error of different methods is also calculated with varied fractional orders from 0.3 to 0.9 at an interval of 0.2. From the results it is clear that the FOSGDD method is efficiently smoothening the signal and calculating its RMS error From Table.3 we can analyse that response of FOSGDD is far better than other methods. |
| In the error comparison, we have analysed that, Proposed FOSGDD is better than all other methods in the both, noise free and contaminated chirp signal experiment. In the noise free case, we have observed that other methods are equally effective with a comparatively high RMSE error but when it comes to comparison between noisy signals, responses of all the other methods are below average with a high error rate. This method is more robust than any other method and it can be easily and quickly be used. |
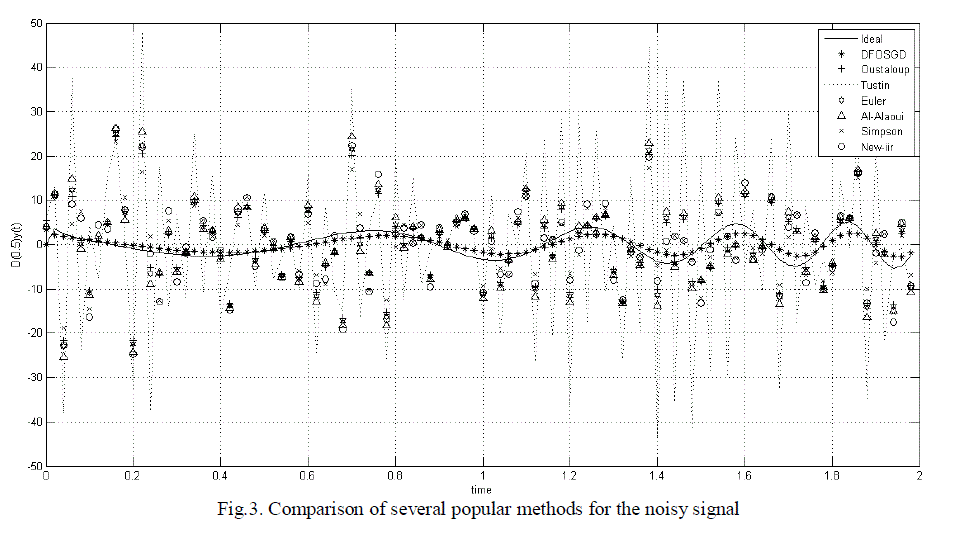
| Furthermore, comparison of different methods for efficient smoothening of noisy signal is performed. Result is shown in Fig.3. In this experiment we have applied signal added with random noise to the differentiator. From the results, it is visible that only proposed method is efficient for computation of derivative of chirp signal. |
| The signal is in normal line is ideal performance and in asterisk is proposed method and rest are of different methods. From the results it is clear that noise is totally removed and from the table it is verified that this method has low RMS error as compared to other methods. |
| For the calculation of root mean square error, we can write as |
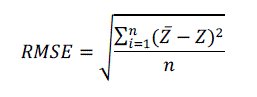 |
| Where estimated signal response, z =ideal signal response and n = number of samples |
| By calculating the RMSE, it is verified that the response of differentiator is better than the other methods, so that it is the only differentiator of its type which will be used for the purpose of smoothening and computation of fractional derivative. |
| In Table.4, computation time of different methods is computed and it shows that FOSGDD consumes very less time in computation. This method consumes very less time for the computation of derivative of the signal so it will be efficiently used in many practical applications. |
CONCLUSION
|
| This paper presents a design method to implement a fractional order differentiator. In this paper we have used least square method and Riemann-Liouville method to implement the proposed method, from the experimental analysis it is clear that it can accurately estimate the fractional order derivative of the different signals, like chirp signal, sinusoidal signal etc. It can accurately smoothen the signal and calculate its fractional order derivative. Another advantage of this method is that, it consume less time in comparison to other methods. As it comes to contaminated signal, it is better than any other method. In future this method can be applied in medical image enhancement. It might be used in biomedical signal processing of electrocardiograph (ECG) and left ventricular pressure (LVP), where numerical differentiation is required to extract information about rapid transients enclosed in the signal. |
Tables at a glance
|
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References
|
- K. S. Miller and B. Ross, “An Introduction to the Fractional Calculus and Fractional Differential Equations”, Wiley, New York, 1993.
- K. B. Oldham and J. Spanier, “The Fractional Calculus”, Academic Press, New York, 1974.
- S. Das, “Functional Fractional Calculus”,Springer, 2011.
- D.Chen, Y. Chen and D. Xue, “Digital Fractional Order Savitzky-Golay Differentiator”, IEEE Transaction on Circuit and System, vol.58, no.11, 2011.
- C.C Tseng, “Design of Fractional Order Digital FIR Differentiators”, IEEE Signal Processing. Letter. vol. 8, no.3, pp.77-79, 2001.
- R. W. Schafer, “What is Savitzky-Golay filter”, IEEE Signal Processing Magazine, vol.28, no. 4, pp.111-117 2011.
- S.C Dutta Roy, “On the realization of a constant argument immitance or fractional operator”, IEEE Transaction Circuit Theory, vol.14, no.3, pp. 264-274, 1967.
- A. Charef, H.H. Sun, Y.Y. Tsao, and B. Onaral, “Fractal system as represented by singularity function”, IEEE Transaction Automation Control, vol.37, no.9, pp.1465-1470, 1992.
- A. Oustaloup, F. Levron, B. Mathieu and F.M. Nanot, “Frequency-band complex non-integer differentiator, Characterization and synthesis”,IEEE Transaction Circuit Systems, vol.47, no.1, pp. 25-39, 2000.
- C.C. Tseng and S.L. Lee, “Design of fractional order digital differentiators using radial basis function”, IEEE Transaction circuit and system, vol. 57, no.7, pp.1708-1718, 2010.
- M. AL-Alaoui, “Novel digital integrator and differentiator”, Electronic Letter, vol.29, no.4, pp.376-378, 1993.
- Y.Q. Chen and K.L. Moore, “Discretization schemes for fractional order differentiator and integrators”, IEEE Transaction Circuit and System, vol.49, no.3, pp.363-367, 2002.
- Y.Q. Chen and B.M. Vinagre, “A new IIR type digital fractional order differentiators”, IEEE Transaction on Signal Processing, vol.83, no.4, pp.2359-2365, 2003.
- S.Samadi, M.O. Ahmed and M.N.S. Swamy, “Exact fractional order differentiator for polynomial signals”, IEEE Signal Processing Letter, vol.11, no.6, pp.529-532, 2004.
- C.C. Tseng, “Improved design of digital fractional-order differentiators using fractional sample delay”,IEEE Transaction on Circuit and System, vol.53, no.1, pp.193-203, 2006.
- R.S. Barbosa, J.A.T. Machado and M.F. Silva, “Time domain design of fractional differ-integrators using least squares”,IEEE Transaction on Signal Processing, vol.86, no.10, pp.2567-2581, 2006.
|