Automorhpic Integrals with Rational Period Functions and Arithmetical Identities

Abstract

In 1961, Chandrasekharan and Narasimhan showed that for a large class of Dirichlet series the functional equation and two types of arithmetical identities are equivalent. In 1992, Hawkins and Knopp proved a Hecke correspondence theorem for modular integrals with rational period function on theta group. Analogous to Chandrasekharan and Narasimhan, in 2015 Sister Ann M. Heath has shown that the functional equation in Hawkins and Knopp context and two type of arithmetical identities are equivalent. She considered the functional equation and showed its equivalence to two arithmetical identities associated with entire modular cusp integrals involving rational period functions for the full modular group. In this paper we extend the results of Sister Ann M. Heath to entire automorphic integrals involving rational period functions on discrete Hecke group.

Keywords

Recurrence; Bernoulli numbers; Bernoulli polynomials; Hypergeometric Bernoulli numbers; Polynomials

Introduction

Let {λ_n} and {μ_n} be two strictly increasing sequences of positive real numbers diverging to ∞, as n → ∞ and let {a_n} and {b_n} be two sequences of complex numbers not identically zero. Consider the Dirichlet series φ and ψ defined by

φ(s) = $\frac{\mathrm{a_n}}{\mathrm{\lambda ^s<sub\; style="position\; :\; relative;\; left:\; -.5em;">n</sub>}}$ and ψ(s) = $\frac{\mathrm{b_n}}{\mathrm{\mu ^s<sub\; style="position\; :\; relative;\; left:\; -.5em;">n</sub>}}$

with finite abscissas of absolute convergence σ_a and σ_b, respectively. Suppose that φ and ψ satisfy the functional equation

Γ(s)φ(s) = Γ(δ − s)ψ(δ − s),                        (1.1)

where δ>0. Chandrasekharan and Narasimhan [1] showed that the functional equation (1.1) is equivalent to the following arithmetical identities (1.2) and (1.3).

$\frac{1}{\mathrm{\Gamma (\rho \; +\; 1)}}$ a_n(x − λ_n)^ρ = $\left(\frac{1}{\mathrm{2\pi }}\right)\rho$ b_n $\left(\frac{\mathrm{x}}{\mathrm{\mu n}}\right)$ \frac{\mathrm{\delta +\rho }}{2}$J$_δ+ρ{4π√μ_nx} + Q_ρ(x),                      (1.2)

where x > 0, ρ ≥ 2β − δ − ½ , J_ν (z) denotes the usual Bessel function of the first kind of order ν,

Q_ρ(x) = $\frac{1}{\mathrm{2\pi i}}$ ∮_c $\frac{\mathrm{\Phi (s)(2\pi )^sx^s+\rho}}{\mathrm{\Gamma (s\; +\; \rho \; +\; 1)}}ds,$| b_n | μ^-β_n < ∞. $\left(-\frac{1}{\mathrm{s}}\frac{\mathrm{d}}{\mathrm{ds}}\right)\rho$ $[\frac{1}{\mathrm{s}}$a_ne^-s√λ_n ] = 2^3δ+ρΓ(δ+ρ+½)π^δ-½ $\frac{\mathrm{b_n}}{\mathrm{(s²+16\pi ²\mu _n)^{\delta +\rho +½}}}+\; R\rho (s),\; \; (1.3)$

where Re s > 0, ρ is non-negative integer satisfying ρ ≥ β − δ − ½ and

R_ρ(s) = $\frac{1}{\mathrm{2\pi i}}$ ∮_c $\frac{\mathrm{\Phi (z)(2\pi )^z\Gamma (2z=2\rho +1)2^-\rho}}{\mathrm{\Gamma (z\; +\; \rho \; +\; 1)}}s-2z-2\rho -1dz$ .

Note that if β>0, then identity (1.3) holds for ρ satisfying ρ ≥ β − δ − ½ ρ ∈ Z ≥ 0.

In [3], Hawkins and Knopp proved a Hecke correspondence theorem for modular integrals with rational period functions on Γ_θ, (generated by Sz = z + 2 and Tz = −1/z), a subgroup of the full modular group Γ(1). In their work, the functional equation takes the form

Φ(2k − s) − i^2kΦ(s) = R_k(s),                        (1.4)

where        Φ(s) = $\left(\frac{\mathrm{2\pi }}{\mathrm{\lambda _n}}\right)-s\Gamma (s)$a_nn^-s

is associated with a modular relation involving rational period function q(z) of the form

F(z + λ) = F(z) and z^−2k F $\left(\frac{\mathrm{-1}}{\mathrm{z}}\right)$ = F(z) + q(z),                        (1.5)

where λ = λ_n = 2 cos $\left(\frac{\mathrm{\pi }}{\mathrm{n}}\right)$ , with 3 ≤ n ∈ ℕ ∪ {∞} and 2k ∈ ℤ.

Analogous to Chandrasekharan and Narasimhan, Sister Ann M. Heath [4] showed that the functional equation in the Hawkins and Knopp context (1.4) and the arithmetical identities are equivalent. To prove her results, she used the fact that the correspondence theorem between the functional equational (1.4) and the associated entire integrals form with rational period function for the full modular group Γ(1). We [9] also used techniques of Chandrasekharan and Narasimhan to prove results analogous to those of Sister Ann M. Heath and established equivalence of two arithmetical identities with functional equation associated with automorphic integrals involving log-polynomial-period functions on the discrete Hecke group.

In this paper we use the techniques of Chandrasekharan and Narasimhan [1] and extend the results of Sister Ann M. Heath [4] to entire automorphic integrals involving rational period functions on discrete Hecke group G(λ). This paper is organized as follows: In section two we review some results concerning, Heck groups, automorphic integrals with rational period function and present some preliminary results. In section three we present our main results with their proofs.

Preliminaries

In this section we review some terms and results that are useful in the coming sections.

Recall that the Hecke group G(λ), where λ ∈ R⁺, is defined as the subgroup of SL₂(R) given by

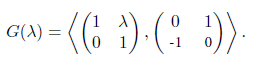
Equivalently G(λ) is generated by the linear fractional transformations S(z) = z + λ and T(z) = − $\frac{1}{\mathrm{z}}$ . The element of G(λ) act on the Riemann sphere as linear fractional transformation, that is Mz = $\frac{\mathrm{az+b}}{\mathrm{cz+d}}$ for

M = $\left(\genfrac{}{}{0ex}{}{\mathrm{a\; \; b}}{\mathrm{c\; \; d}}\right)$ ∈ G(λ), and z ∈ ℂ ∪{∞},

thus M and −M can be identified with the same linear fractional transformations. Hecke [6] showed the group G(λ) is discrete (operates discontinuously) as a set of linear fractional transformations on the upper half plane

ℋ = {z = x + iy : y > 0} if and only if either λ>2 or λ = λ_p:= 2cos $\left(\frac{\mathrm{\pi }}{\mathrm{n}}\right)$ , with 3 ≤ p ∈ ℕ ∪{∞}. For λ ≥ 2 and λ=λ_p, we have the following relations respectively,

T² = −I, T² = (S_λp T)^p = −I.

It is clear that G(λ₃) = G(1) = Γ(1) is the full modular group, and G(λ_∞) = Γ_θ is the familiar theta group.

Suppose F (z) is a meromorphic function in the upper half planHe t hat satisfies (1.5). Further assume that F has Fourier series expansion of the form

F(z) = a_me^2πimz/λ,                        (2.1)

where ℑz = y > y_o ≥ 0 and ν ∈ ℤ. The function F is called an automorphic integral of weight 2k for the Hecke group G(λ), with rational period function (RP F ) , q(z). If q ≡ 0 then F is an automorphic form of weight 2k on G(λ). If F is an automorphic integral and holomorphic in H (that is, ν ≥ 0) and satisfies the growth condition

| F(z) | ≤ C (| z |^α + y^−β) , ℑ(z) = y>0,

for some constants C, α, β, > 0, and z ∈ ℋ one can show that the cofficients a_m in (2.1) satisfy

a_m = 𝒪(m^β), m → ∞.

In this case, F is called an entire automorphic integral of weight 2k on G(λ) with rational period function q.

For M = $\left(\genfrac{}{}{0ex}{}{\mathrm{*\; \; *}}{\mathrm{c\; \; d}}\right)$ ∈ G(λ) the stroke or slash operatoris defined by

F | M := F |^M_2k = (cz + d)^−2k F(Mz).

Thus the second automorphic relation (1.5) can be expressed as F |T = F + q. In general, for any M in G(λ) there is a corresponding period function qM such that F |M = F + q_M . The slash operator satisfies F |M₁M₂ = (F |M₁)|M₂ for M₁, M₂ ∈ G(λ) and hence the family of periodic functions{ q_M : M ∈ G(λ} are related by

q_M1M2 = q_M1| M2 + q_M2 , M1, M2 ∈ G(λ).                        (2.2)

Using the relation T² = −I,(2.2 imposes a relation on the (RPF) q,

q|T + q = 0.                        (2.3)

And using the relation (S_λpT)^p = −I for tλ = λ_p = 2 cos $\left(\frac{\mathrm{\pi }}{\mathrm{p}}\right)$ , p ∈ ℤ, p ≥ 3, imposes another condition on (RPF) q,

q | (S_λpT)^p−1 + q | (S_λpT)^p−2 + · · · + q | (S_λpT) + q = 0.                        (2.4)

Marvin Knopp [7] proved that the finite poles of a rational period function on Γ(1) are only at 0 or real quadratic irrationals. He also showed thaqt iisf a RPF of weightk 2k > 0 with poles in Q, then for some constanαts α₀, α₁ ∈ C,

q(z) =

Observe that if F(z) ≡ −α₀, then (F|T ) (z) = F(z) + q(z) implies that z^−2kF $\left(\frac{\mathrm{-1}}{\mathrm{z}}\right)$ − F(z) = q(z) and hence q(z) = α₀ (1 − z^−2k)

Thus we consider q(z) = α₀ (1 − z^−2k) as the trivial period function of weight 2k ∈ R.

The following lemma is stated in the work of Hawkins and Knopp [3], where their underlying groiusp Γ_θ and generalized to the general Hecke group and multiplier system by Hassen [2].

Lemma 2.1. Nontrivial rational period function on the Hecke groups satisfying (2.3) and (2.4) exists only if the weight 2k is an integer.

Wendell-Culp-Ressler in ([8], Lemma 3) showed that the poles of any rational periodic functionq of weight 2k, k ∈ Z⁺ on With appropriate modifications to fit for the current context of functions on G(λ), the work of Hawkins and Knopp [3] can be used to state a special form of RP F for the solution of (2.3). This form is given by the following lemma.

Lemma 2.2. For r ∈ ℤ, α_j ∈ ℝ \ {0}, C_r, C_rj∈ ℂ for j = 1, 2 ......., p, let f_r(z, 0) = z^−r − (−1)^r z^−2k+r, and

f_r(z, α_j) = (z − α_j)^−r − (−1)^r α_j^−r z^−2k+r $\left(z\; +\frac{1}{\mathrm{\alpha _j}}\right)$ ^−r. Then

q(z) = C_rf_r(z, 0) + C_rjf_r(z, αj) and satisfies q | T + q = 0.                        (2.5)

Theorem 2.1. Suppose F is an entire automorphic integral function of weight 2k, k ∈ Z⁺ for G(λ) with (RPF ) q(z), where q has the form described by Lemma 2.2. Suppose further that F has a Fourier series expansion of the form

F(z) = a_me^2πimz/λ, with a_m = 𝒪(m^β) β > 0, m → ∞.                        (2.6)

φ(s) = a_mm^−s and Φ(s) = $\left(\frac{\mathrm{2\pi }}{\mathrm{\lambda }}\right)-s$ Γ(s)φ(s), s = σ + it.                        (2.7)

Then Φ(s) has a meromorphic continuation to the whole complex plane and can be expressed in the form of Φ(s) = D(s) + D⁰(s) + E⁰(s) + E^H(s) + E^B(s),

where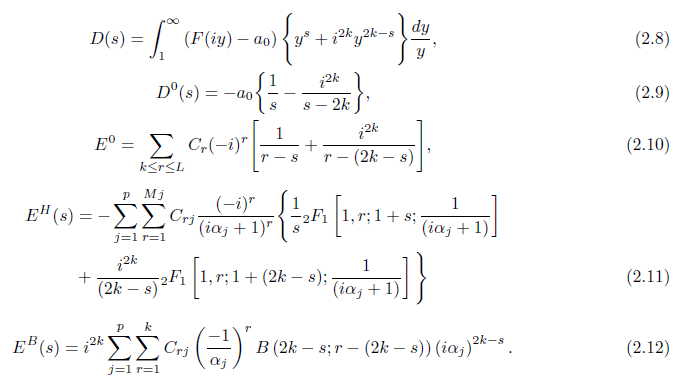

Moreover, Φ(s) satisfies the functional equation

Φ(2k − s) − i^2kΦ(s) = R(s) , where                        (2.13)

R(s) = E^B(2k − s) − i^2kE^B(s)

and ₂F₁ [a, b, c; z] is the hypergeometric function and B(a, b) is the Beta function.

The proof of Theorem 2.1 is similar to that of Hawkins and Knopp [3], with appropriate modifications for the more general group

λ_p = 2 cos > 0. $\left(\frac{\mathrm{\pi }}{\mathrm{p}}\right)$

Corollary 2.1. Suppose Φ(s), D⁰(s), D(s), E⁰(s), E^H(s) and E^B(s) are given as in Theorem 2.1. Then (a) Φ(s) is bounded uniformly in σ in lacunary vertical strips of the form

S = {s = σ + it : 2k − δ ≤ σ ≤ δ; |t| ≥ to > 0}.

(b) δ in (a) can be chosen so that the poles of Φ(s) lying with in the lines s = (2k − δ) + it and s = δ + it are listed below in the sets;

S₀ = {0, 2k}, S_E0 = {2k − L, 2k − L + 1, ..., k − 1, k, k + 1, ..., 2k, ..., L},
S_H = {[2k − δ], ..., 0}, S_B = {[2k − δ], ..., 2k − L, ..., 2k − 1}.

The poles of Φ(s) in each set arise from D⁰(s), E⁰(s), E^H(s) and E^B(s) respectively. (c) The residues of Φ(s) are given by the formula

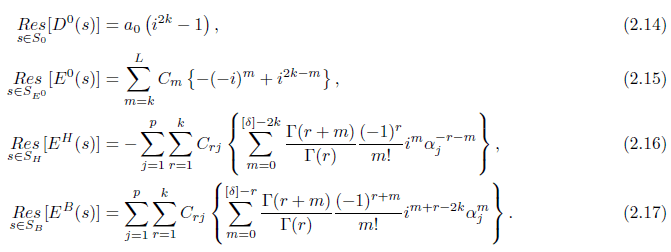
Before we state and prove our main results, we state Perron’s formula as Lemma 2.3 below (see [1] for details.) We shall also use the convention of writing

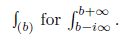
Lemma 2.3. Let σ₀ be the abscissa of absolute convergence for φ(s) = a_mλ^−s_mand {λm} be a sequence of positive real numbers tending to ∞ as m → ∞. Then for k ≥ 0, σ > 0 and σ₀,

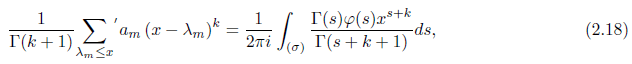
where the prime′ on the summation sign indicates that if k = 0 and x = λ_m for some positive integer m, then we count only ½a_m.

The evaluation of the integral in (2.18) of Lemma 2.3, we consider a positively oriented rectangular contour formed by

[(2k − σ) − iT, σ − iT ], [σ − iT, σ + iT ], [σ + iT, (2k − σ) + iT ], [(2k − σ) + iT, (2k − σ) − iT ],

use Stirling’s approximation formula for the gamma function, Phragmen-Lindelo¨f theorem [5] and apply Cauchy Residue theorem where in all cases the parameters are choosen appropriately to satisfy the conditions. Note that we use this in several places and cite it as [5].

Results

In this section, we shall use the techniques of Chandrasekharan and Narasimhan in [1] to extend the first result in [4] to entire automorphic integrals on discrete Hecke groups G(λ).

Theorem 3.1. (F irstEquivalence) . Let Φ(s) and R(s) be as in Theorem 2.1. Then the functional equation

Φ(2k − s) − i^2kΦ(s) = R(s)                        (3.1)

is equivalent to the identity

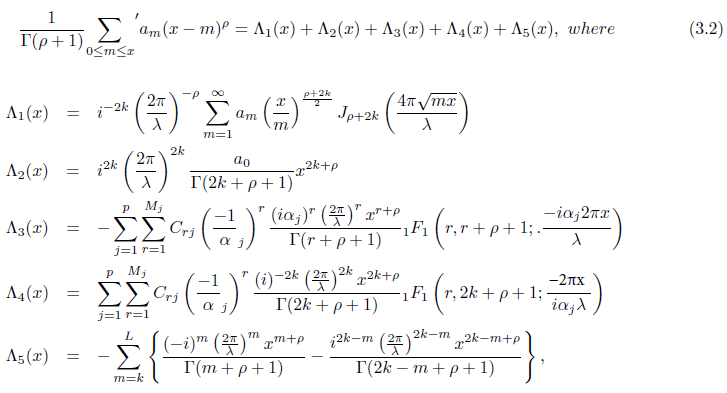
x > 0, ρ ≥ 2β − 2k − ½ , and β is a number for which $\frac{\mathrm{|a_m|}}{\mathrm{m^\beta}}$ < ∞.

Proof. We use [5] to arrive at

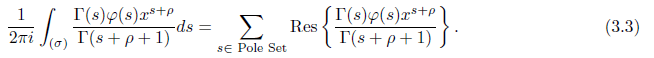
Hence by using again [5] (3.3) can now be written as

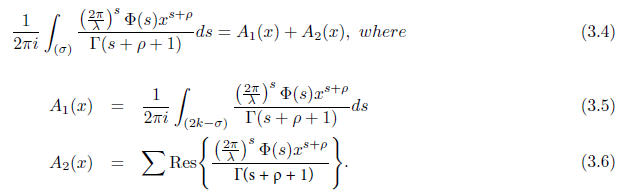
We now show that the functions A1(x) and A2(x) can be expressed respectively as

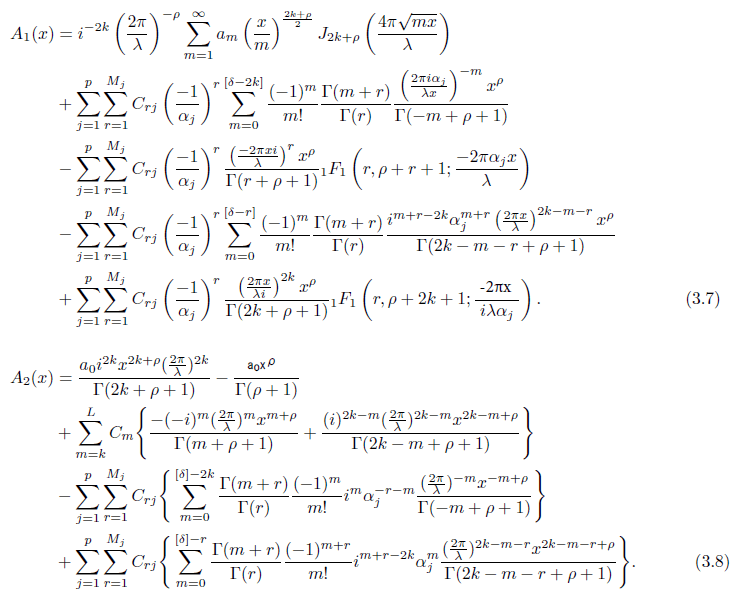
Observe that using the functional equation Φ(2k − s) − i^2kΦ(s) = R(s), we have

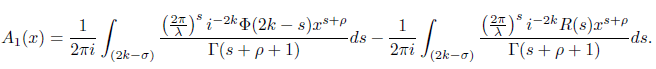
Since Φ(s) = $\left(\frac{\mathrm{2\pi }}{\mathrm{\lambda }}\right)-s$ Γ(s)φ(s), and denoting the first integral by I(x) we see that

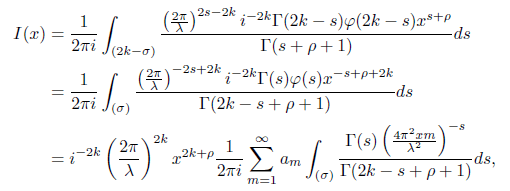
where we have used change of variable froms to 2k − s, in the first integral. Letting $\frac{\mathrm{w}}{2}$ = s, ν = 2k + ρ, and simplifying expressions, we obtain

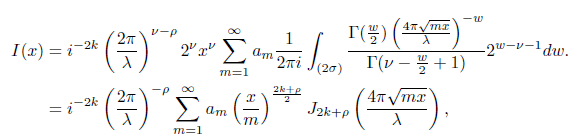
provided that ρ > σ − 2k and σ > 2k, k ∈ Z. Note also that we have used the definition of the Bessel J-function here. Now we evaluate the second integral denoting by H(x) and using the expression for R(x) as follows

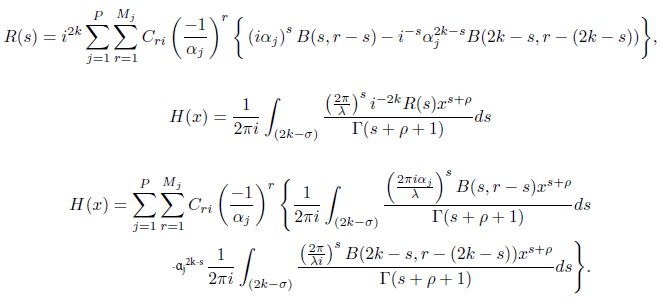
Using the properties of the beta function and after some algebraic manipulations, we have

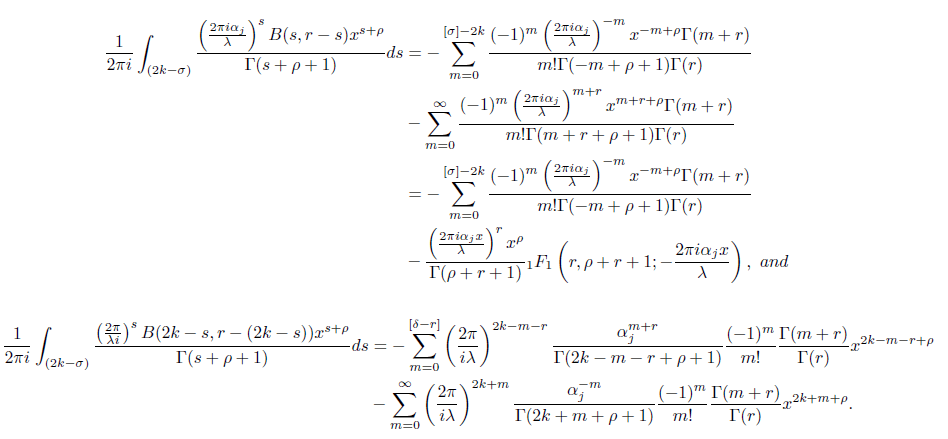
Using the properties of hypergeometric series and simplifying, we get

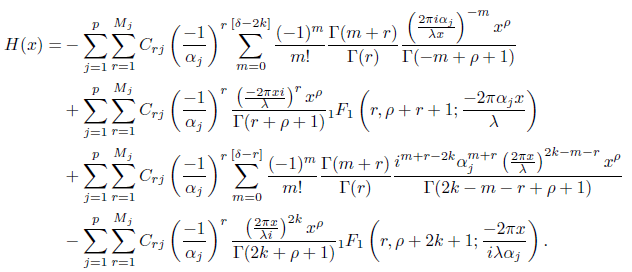
Since A₁(x) = I(x) − H(x), we have proved (3.7) and proceed to computing A₂(x) as follows.

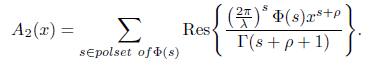
From theorem 2.1, Φ(s) has been expressed in terms of D⁰(s), E⁰(s), E^H(s), and E^B(s). Thus A₂ can be expressed as follows

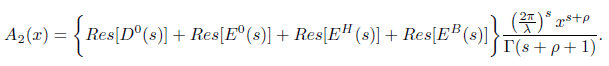
Using formula (2.14), (2.15), (2.16)and (2.17) we obtain the following and hence (3.8) is proved.

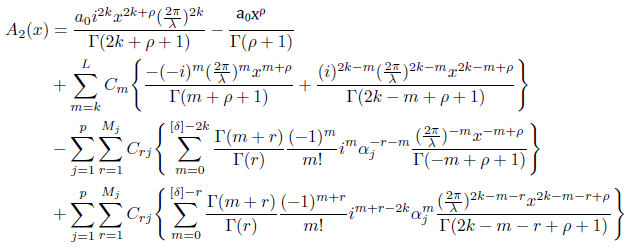
Finally, we now express the integral in the right-hand side of (3.4) as

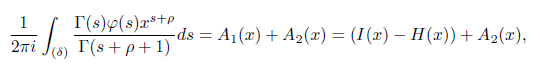
and using the expressions for A₁(x) and A₂(x). [See (3.7) and (3.8) respectively] we obtain

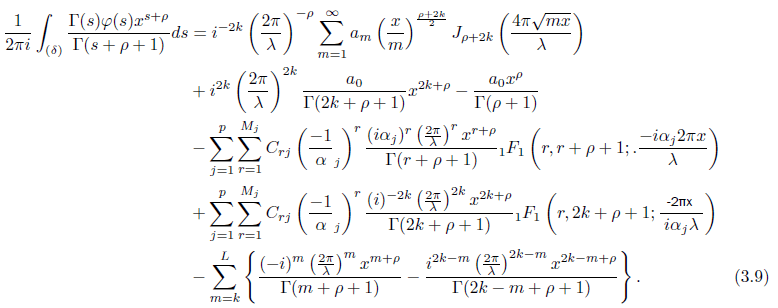
Therefore, for ρ ≥ 0, and $\frac{\mathrm{\rho \; +\; 2k}}{2}$ > δ we get the identity (3.2).

Now we prove the converse of the theoremo. Tthis end supposeF (z) is an entire automorphic integral with ao uFrier series expansion for z ∈ H and satisfies the relatio

F(z) = a_me^2πimz/λ,

z^−2kF $\left(\frac{\mathrm{-1}}{\mathrm{z}}\right)$ = F(z) + q(z),                        (3.10)

where q(z) is the rational period function given by Lemma (2.2). Then by (3.10) and the Fourier expansion of F we have

z^−2ka_me^−2πim/λz = a_me^2πimz/λ + q(z).

Letting z = $\frac{\mathrm{iy\lambda }}{\mathrm{2\pi }}$ , y > 0, then we get

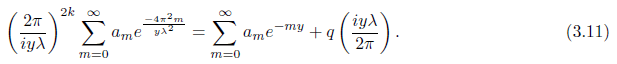
To prove the converse it suffices to show that (3.2) implies (3.11). To this end we consider six integrals defining L₁(y) · · · , L₆(y), corresponding to the six expressions occurring in (3.9). We evaluate all the integrals by interchanging integration and summation which can be justified

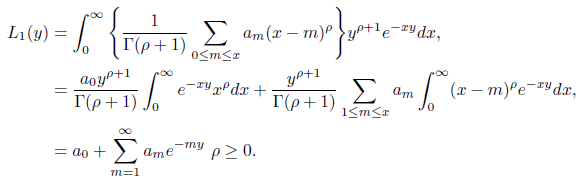
Similarly L₂(y) for $\frac{\mathrm{\rho \; +\; 2k}}{2}$ ≤ β and applying formula (??) we get

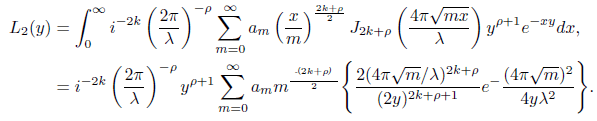
Thus with simple algebraic manipulations we obtain

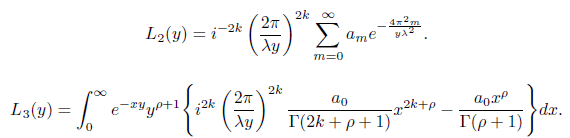
Using integration by substitution and the standard integral representation of Γ(s) we get

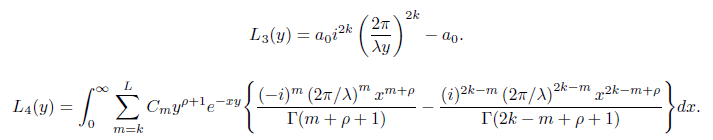
After evaluating and simplifying we obtain

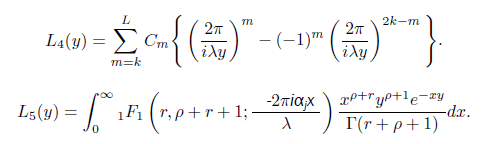
Using the series representation of the hypergeometric function for λy > 2πα_j , we obtain

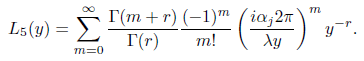
This series converges absolutely for λy > 2πα_j. In a Similar wa,y we compute L₆ as follows

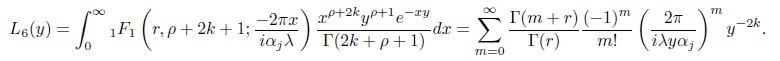
This series converges absolutely for y > $\frac{\mathrm{2\pi }}{\mathrm{\lambda \alpha _j}}$ . Combining the results of the integrals for L₁(y), L₂(y), · · · , L₆(y) respectively we have

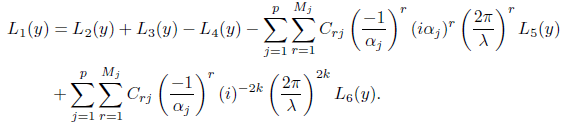
Thus after simple algebraic manipulations, we see that the identity in (3.9) implies

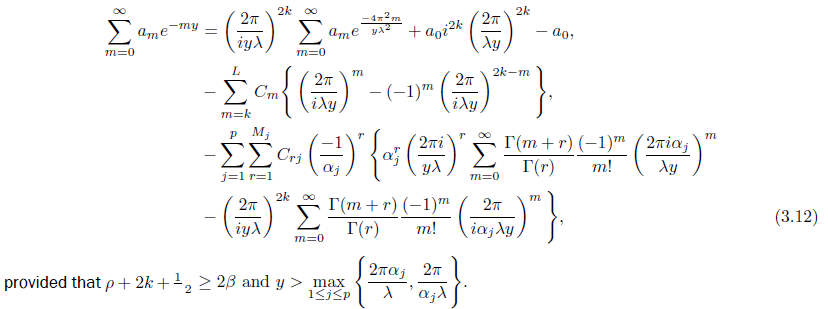
Recall that the rational periodic function in Lemma 2.1.

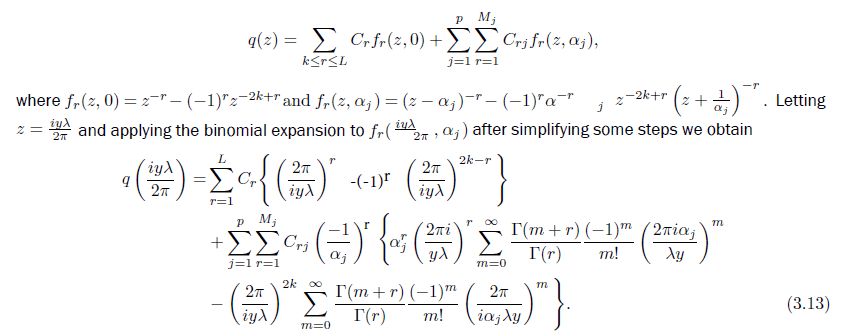
Since F(z) has a Fourier expansion of the form a_me^2πimz/λ and q $\left(\frac{\mathrm{iy\lambda }}{\mathrm{2\pi }}\right)$ is represented (3.13), (3.12) may be written as

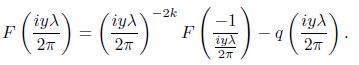
Hence by the identity theorem the automorphic transformation

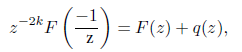
follows for z ∈ H. This concludes the proof of the equivalence of the functional equation to the identity (3.9). Theorem 3.2. (Second Equivalence) Let Φ(s) and R(s) as in Theorem 2.1 then the functional equation

Φ(2k − s) − i^2kΦ(s) = R(s)                        (3.1)

is equivalent to the identity

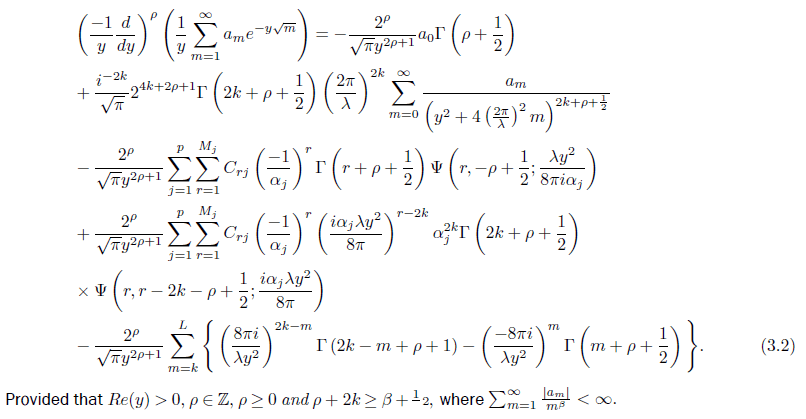
Proof. By theorem .31 the identity (3.2) is equivalent to the functional equation (.13). Hence to prove this theorem it suffices to show that (3.1) implies (3.2) and (3.2) in turn implies (3.1).

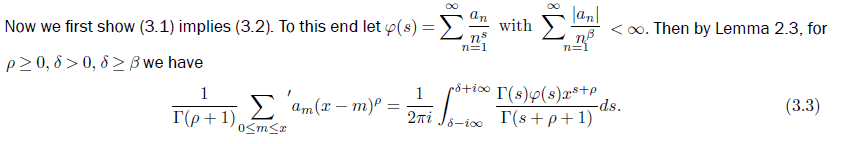
As in Chandrasekharan and Narasimhan ([1] page 9), we multiply (3.3) by e^−y√xx^−½ and integrating with respect to the variable x from x = 0 to ∞; and further assuming δ > 2k, where Res = δ is the vertical path of integration. Now choose δ = β + P, where P ∈ Z, and P is large enough to guarantee δ > 2k and δ ∉ Z to have

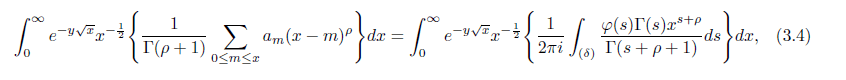
with ρ+2k ≥ δ + ½ , and y ∈ ℝ⁺. Chandrasekharan and Narasimhanin [1] for ρ+2k + ½ ≥ β and λ_n sequence of positive real numbers; λ_n → ∞, showed the identity

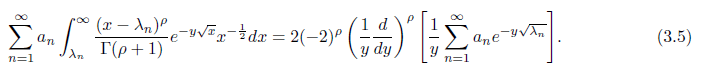
Then put λn = m in (3.5) to have

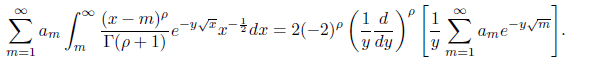
Since Φ(s) = Γ(s)φ(s) $\left(\frac{\mathrm{2\pi }}{\mathrm{\lambda }}\right)-s$ , where Res > β and $\frac{\mathrm{|a_m|}}{\mathrm{m^\beta}}$ < ∞, the right-hand side of (3.3) becomes

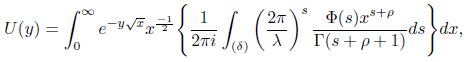
for δ ≥ β. Interchanging the order of integration for ρ ≥ 0 we obtain

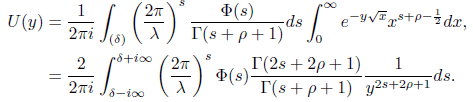
Using the properties of Γ function we have

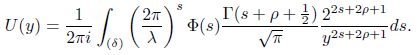
Using [5] we evaluate U (y) and have

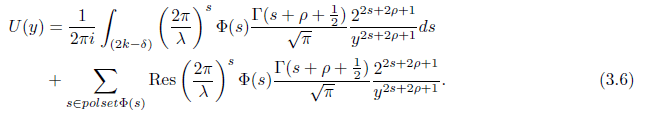
Denote the first and second integrals as T₁(y) and T₂(y) respectively so that U(y) = T₁(y) + T₂(y). Using the identity, Φ(s) = i^−2k (Φ(2k − s) − R(s)) , and substituting in to the integrand of T₁(y), we can write as

T₁(y) = V₁(y) − V₂(y),

where V₁(y) and V₂(y) are given as

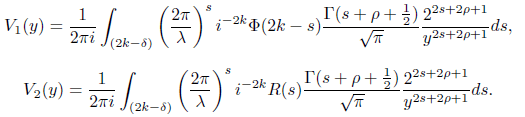
Using the substitution ϑ = 2k − s and Φ(ϑ) = $\left(\frac{\mathrm{2\pi }}{\mathrm{\lambda }}\right)-\vartheta$ Γ(ϑ)φ(ϑ), where φ(ϑ) = $\frac{\mathrm{a_m}}{\mathrm{m^\beta}}$ replacing ϑ by −ϑ, we have

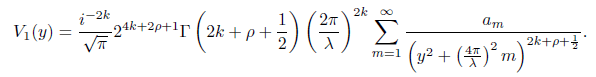
The series converges fory > 0, provided 2k + ρ − ½ > β. Since δ ≥ β the series converges absolutely for ρ ≥ δ − 2k + ½.

Replacing the beta function by its equivalent Γ function and replacinRg( s) by its equivalent representation we have

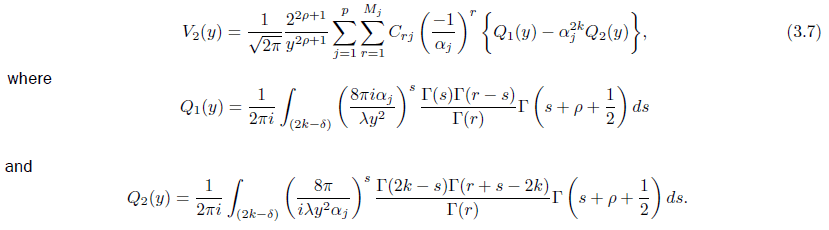
Using [5] we evaluate Q1(y) and obtain

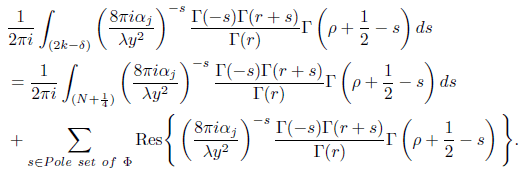
It can be easily shown that the integral on the right-hand side tends to zero as N tends to ∞. Thus evaluating the residue of the poles we have

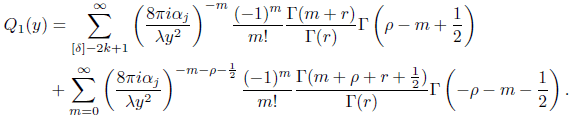
Again using properties of the Γ function and simplifying we obtain

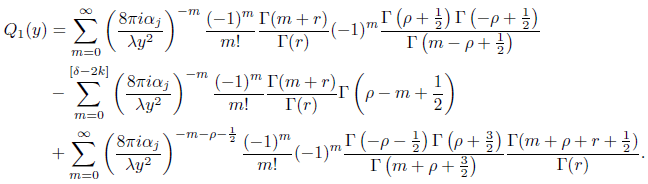
Using series representation of the confluent hypergeometric function we get

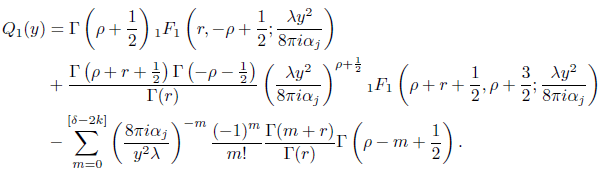
Using the the confluent hypergeometric function of the second kind we have

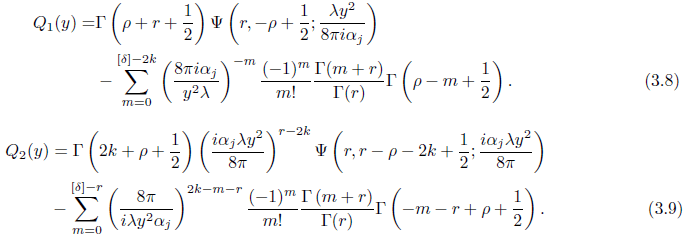
Thus for ρ ≥ 0, ρ ∈ ℤ, ρ + 2k ≥ δ + ½, δ > 2k and y ∈ ℝ⁺ the functional equation in (3.1) implies

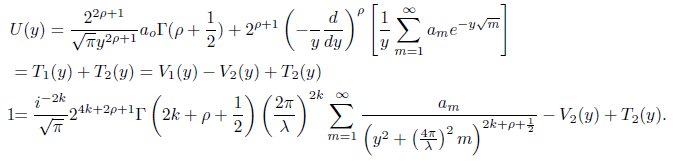
Equating the left-hand and right-hand side expression we obtain

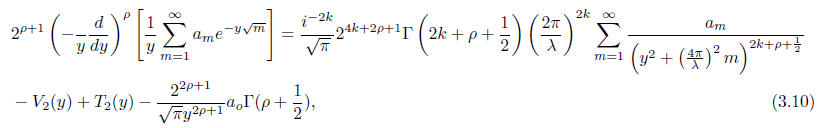
where T₂(y) and V₂(y) are given by (3.6) and (3.7) respectively. We can also get an explicit formula for V₂(y) from (3.6) and (3.8).

Using the expression for T₂ from (3.6) and the residue of Φ(s) from theorem 2.1 we have

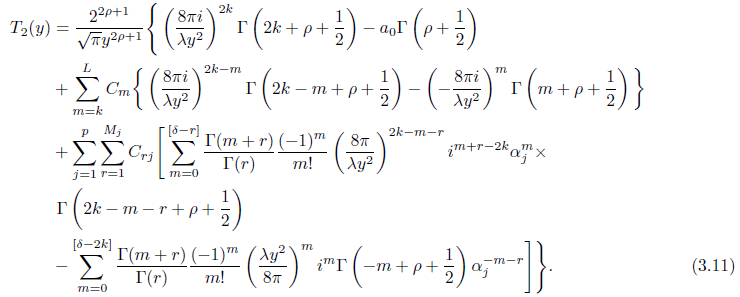
Now substituting (3.11) into (3.10) for T₂(y) and by substituting the respective expressions (3.8), (3.9) into V₂(y), we obtain the identity (3.2) and this completes the proof of implication part.

To prove the converse we only show (3.2) implies (3.1). Multiply (3.2) by e^y√x, with Rey > 0 and x > 0 and integrate the expression along vertical path Res = ϑ, where ϑ > 0. The left hand side (3.2) can be

evaluated using the formula ([1], page 9)

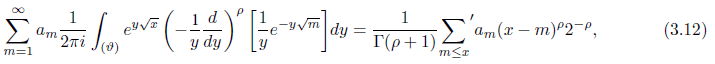
For the right-hand side of (3.2) we compute the integral of each term one by one. So put the first

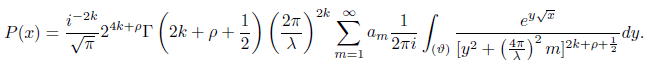
Using Sterling formula and simplifying we obtain

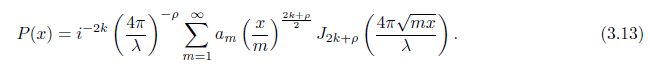
Put the second term

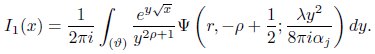
Using the integral in (??) we have

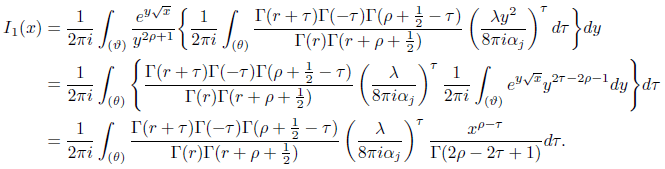
Using properties of the Γ function we obtain

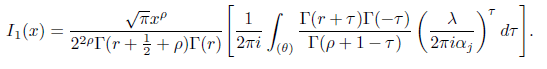
Using [5] we obtain

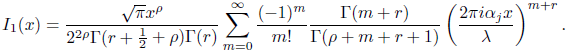
Therefore, we conclude that

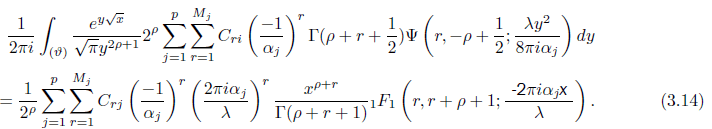
Next put

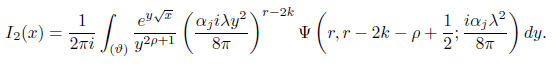
For fixed r, −r < θ < −r + ½ and −π/2 ≤ arg $\left(\frac{\mathrm{i\alpha _j\lambda ²}}{\mathrm{8\pi }}\right)$ , using the integral representation of confluent hyper-geometric function of the second kind we get

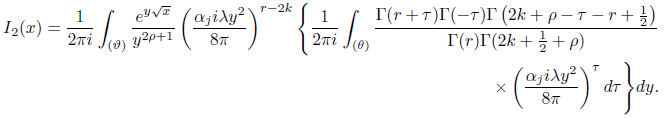
By interchanging the order of integration which can be justified we obtain

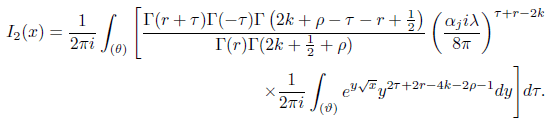
Computing the last integral and simplifying we obtain

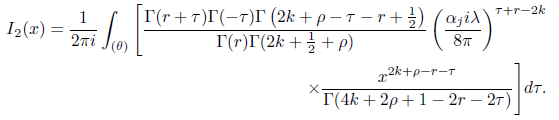
Using properties of the Γ function we obtain

Using [5]) we obtain

Thus using this result for I₂(x) we find that

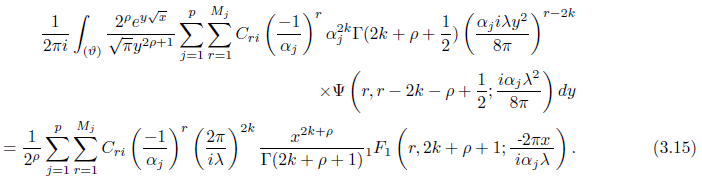
Put the third term as I₃(x) which is given by

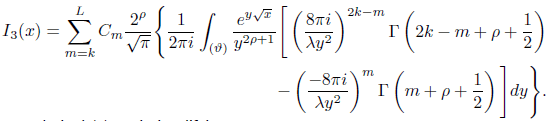
Evaluating each integrals in I₃(x) and simplifying, we get

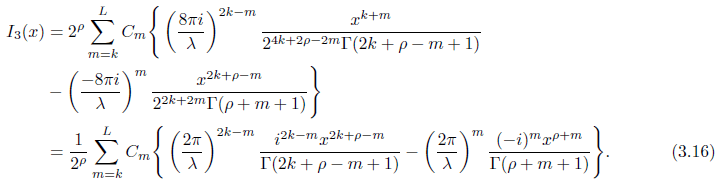
Finally we evaluate the last term in (3.2) which we denote by I₄(x) as

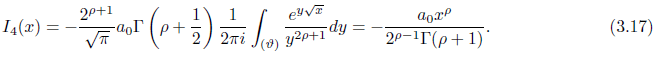
Thus combining the results in (3.13), (3.14), (3.15), (3.16), and (3.17) we obtain

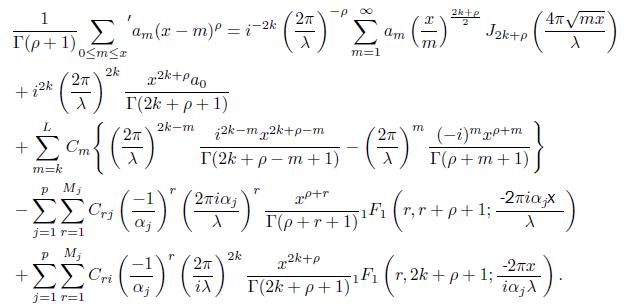
This completes the proof of the converse and therefore, the proof of theorem is completed.

References

1. Chandrasekharan K, et al. Hecke’s functional equation and arithmetical identities. Ann Math. 1961;74:1-23.

   [Crossref]

2. Hassen A, et al. Log-polynomial period function for Hecke groups. Ramanujan J. 1999;3:119-151.

   [Crossref] [Google Scholar]

3. Hawkins J, et al. A Hecke correspondence theorem for automorphic integrals with rational period functions. Illinois J Math. 1992;36:178-207.

   [Google Scholar]

4. Heath SA, et al. Dirichlet series with functional equations and arithmetical identities. Ramanujan J. 2016;41:115-46.
5. Berndt BC, et al. Hecke’s Theory of Modular forms and Dirichlet series. World Sci Res. 2008.

   [Google Scholar]

6. Hecke E, et al. Dirichlet series, modular functions, and quadratic forms. Edwards Brothers Publisher. 1938:48.
7. Knopp M, et al. Rational period functions of the modular group II. Glasgow Math J. 1981;22:185-197.

   [Crossref] [Google Scholar]

8. Resseler W, et al. A Hechek Correspondence Theorem for Automorphic Integrals with symmetric Rational period Functions on Hecke Groups. Franklin and Marshal college, Lancaster. 2008.
9. G/Egziabher T, et al. Automorphic integrals with log-polynomial period functions and arithmetical identities. Math investig. 2023.