In this paper, we have discussed Government Job Selection procedure in India through Bayes’ theorem, or the related likelihood ratio, is the key to almost any procedure for extracting information from data. Bayes’ Theorem lets us work backward from measured results to deduce what might have caused them. It will be the basis of most of our later model building and testing [17].
Keywords |
| Bayes’ Theorem, Strength, Certainty, and Coverage Factor, Flow graph. |
I . INDTRODUCTION OF BAYES’ THEOREM |
| Bayes’ Theorem, or the related likelihood ratio, is the key to almost any procedure for extracting information from
data. Bayes’ Theorem lets us work backward from measured results to deducewhat might have caused them. It will be
the basis of most of our later model building and testing. It UCalgary (2003) is the work of Rev. Thomas Bayes
(St.Andrews, 2003), about whom only a modest amount is known, but he has the perhaps unique distinction that twothirds
of his publications were posthumous and the remaining third anonymous. |
Every decision table describes decisions (actions, results etc.) determined, when some conditions are satisfied. In other
words each row of the decision table specifies a decision rule which determines decisions in terms of conditions. In
 |
 |
II . RELATED WORK |
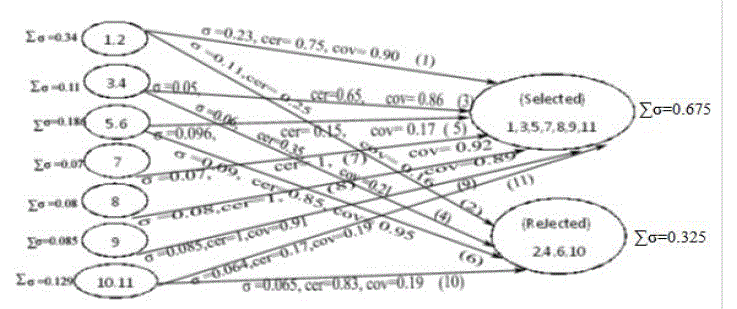
| In this article we will illustrate an idea which is based on Government job selection in India. Here, we have taken 1000
examination candidates (X1,X2,…..,X11) who are preparing them for government job examination in India. For some
government rules each candidate have to fulfil each condition or criteria for getting government job in India. These
conditions are K=Knowledge/ Intelligence, C=Cast, D= Degree, M=Percentage of marks, E= exam Rank. If each
criteria is satisfy then candidate will selected for government job. In Table one the value of each criteria based on Md=
Medium, Gd= Good, Vgd= Verygood , ST= Schedule Tribe, SC= Schedule Cast, Gen= General, Hnd=Physical
Handicap, OBC= Other Backward Cast, Passed and Fail. |
III . DECISION ALGORITHM ASSOCIATED WITH RESPECT OF TABLE 1 |
| X1)if (k=Md, C= ST, D=Md, M= Md, E=Pass) then (Decision is Selected) |
| X2) if (k=Md, C= Gen, D=Md, M=Md, E=Fail) then (Decision is Rejected) |
| X3) if (k=Gd, C= SC, D=Gd, M=,Gd, E=Pass) then (Decision is Selected) |
| X4)if (k=Md, C= Gen, D=Gd, M= Gd, E=Fail)then (Decision is Rejected) |
| X5)if (k=Vgd, C= Gen, D=Vgd, M=Vgd, E=Pass) then (Decision is Selected) |
| X6)if (k=Md, C= Gen, D=Vgd, M= Gd, E=Fail) then (Decision is Rejected) |
| X7)if (k=Vgd, C= Gen, M=Vgd, E=Pass) then (Decision is Selected) |
| X8)if (k=Vgd, C= ST/SC, E=Pass) then (Decision is Selected) |
| X9)if (k=Md, C= Hnd, E=Pass) then (Decision is Selected) |
| X10)if (k=Gd, C= OBC, D=Gd, M=Gd, E=Fail) then (Decision is Rejected) |
| X11)if (k=Gd, C= OBC, D=Vgd, M=Vgd, E=Pass) then (Decision is Selected) |
| Now Let Calculate The Inverse Decision Algorithm in below: |
| X1’)if(Decision is Selected) then (k=Md, C= ST, D=Md, M= Md, E=Pass). |
| X2’) if (Decision is Rejected) then (k=Md, C= Gen, D=Md, M= Md, E=Fail) |
| X3’) if (Decision is Selected) then(k=Gd, C= SC, D=Gd, M=,Gd, E=Pass) |
| X4’)if(Decision is Rejected) then (k=Md, C= Gen, D=Gd, M= Gd, E=Fail) |
| X5’)if(Decision is Selected) then (k=Vgd, C= Gen, D=Vgd, M=Vgd, E=Pass) |
| X6’)if (Decision is Rejected) then (k=Md, C= Gen, D=Vgd, M= Gd, E=Fail) |
| X7’)if(Decision is Selected) then (k=Vgd, C= Gen, M=Vgd, E=Pass) |
| X8’)if(Decision is Selected) then (k=Vgd, C= ST/SC, E=Pass) |
| X9’)if(Decision is Selected) then (k=Md, C= Hnd, E=Pass) |
| X10’)if(Decision is Rejected) then ( k=Gd, C= OBC, D=Gd, M=Gd, E=Fail) |
| X11’)if(Decision is Selected) then (k=Gd, C= OBC, D=Vgd, M=Vgd, E=Pass) |
CONCLUSION |
| In this paper, from above discussion we can reach ultimate solution that for getting Government job in India some
criteria are most important to qualify the examination test. With respect of some important criteria we got “X6,
X10,X7,X9” are eligible to clear the exam test but X2,X5,X11,X4 these candidates are not properly eligible to clear
the exam for getting the job and those we are succeed to achieve the goal through Bayes’ Theorem which actually
expertism evolutionary method which help to reach actual decision. |
Tables at a glance |
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
| |
Figures at a glance |
 |
| Figure 1 |
|
| |
References |
- Duda, R.O. and Hart, P.E. Pattern Classification and Scene Analysis, Wiley, NewYork, 1973.
- Good, I.J.,The Estimation of Probabilities: An Essay on Modern Bayesian Methods. M.I.T. Press. 1965.
- Greco, S., Matarazzo, B. and Slowinski, R. Parameterized rough set model using rough membership and Bayesian confirmation measures,International Journal of Approximate Reasoning, 49, 285-300, 2009.
- Herbert, J.P. and Yao, J.T. Game-theoretic risk analysis in decision-theoretic rough sets, Proceedings of RSKT'08, LNAI 5009, 132-139, 2008.
- Herbert, J.P. and Yao, J.T. Game-theoretic rough sets, Fundamental Informaticae, 2009.
- Pawlak, Z. Rough sets, International Journal of Computer and Information Sciences, 11, 341-356, 1982.
- Pawlak, Z. Rough Sets, Theoretical Aspects of Reasoning about Data, Dordrecht: Kluwer Academic Publishers, 1991.
- Pawlak, Z., Wong, S.K.M. and Ziarko, W. Rough sets: probabilistic versus deterministic approach, International Journal of Man-Machine Studies,29, 81-95,1988.
- Pawlak, Z. and Skowron, A. Rough membership functions, in: Yager, R.R., Fedrizzi, M. and Kacprzyk, J., Eds., Advances in the Dempster-ShaferTheory of Evidence, John Wiley and Sons, New York, 251-271, 1994.
- Slezak, D. Rough sets and Bayes factor, LNCS Transactions on Rough Sets III, LNCS 3400, 202-229, 2005.
- G. E. P. Box, G. C. Tiao: Bayesian Inference in: Statistical Analysis, John Wiley and Sons, Inc., New York, Chichester, Brisbane, Toronto,Singapore, 1992
- M. Berthold, D. J. Hand: Intelligent Data Analysis, an Introduction, Springer-Verlag, Berlin, eidelberg, New York, 1999
- Z. Pawlak: Rough Sets and Decision Algorithms, in: W. Ziarko, Y. Y. Yao (eds.), Second International Conference, Rough Sets and Current Trends in Computing, RSCTC 2000, Banff, Canada, October 2000, LNAI 2000, 30-45
- E. W. Adams: The Logic of Conditionals, an Application of Probability to Deductive Logic. D. Reidel Publishing Company, Dordrecht, Boston,1975
- T. Bayes: An essay toward solving a problem in the doctrine of chances, Phil. Trans. Roy. Soc., 53, 370-418; (1763); Reprint Biometrika 45, 296-315, 1958
- J. M. Bernardo, A. F. M. Smith: Bayesian Theory, Wiley Series in Probability and Mathematical Statistics, John Wiley & Sons, Chichester, New York, Brisbane, Toronto, Singapore, 1994.
- Chilin Shih, Greg Kochanski, “Bayes’ Theorem”, September 15, 2006.
|