International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Big Integer Multiplication with CUDA FFT (cuFFT) Library

Hovhannes Bantikyan
Department of Computer Systems and Informatics, State Engineering University of Armenia, Yerevan, Armenia
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

It is well recognized in the computer algebra theory and systems communities that the Fast Fourier Transform (FFT) can be used for multiplying polynomials. Theory predicts that it is fast for “large enough” polynomials. The basic idea is to use fast polynomial multiplication to perform fast integer multiplication. We can achieve really fast FFT multiplication on GPU with parallel FFT implementation, in this case with cuFFT. Here we provide cuFFT multiplication and its comparison with well known fast big integer arithmetic libraries (.net BigInteger, GMP, IntX). We also compare our results with results of other papers in this area. Experiments showed, that cuFFT multiplication is becoming faster than all other tested methods, when we deal with about 2^15 digit integers.

Keywords
Fast Fourier Transformation; Big Integer Multiplication; GPGPU; CUDA programming; cuFFT

I. INTRODUCTION
Multiplying big integers is an operation that has many applications in Computational Science. Many cryptographic algorithms require operations on very large subsets of the integer numbers. A common application is public-key cryptography, whose algorithms commonly employ arithmetic with integers having hundreds of digits [1]. Arbitrary precision arithmetic is also used to compute fundamental mathematical constants such as π to millions or more digits and to analyze the properties of the digit strings or more generally to investigate the precise behavior of functions such as the Riemann zeta function where certain questions are difficult to explore via analytical methods. Another example is in rendering fractal images with an extremely high magnification, such as those found in the Mandelbrot set [2].
Three most popular algorithms for big integers multiplication are Karatsuba-Ofman [3], Toom-Cook [4] and FFT multiplication [5] algorithms. Classical multiplication operation has O(n2) complexity, where n is the number of digits. By using polynomial multiplication with FFT, which has time complexity O(nlogn), we can significantly reduce the time it takes for multiplication. For such large data volume based applications the Graphics Processing Unit (GPU) based algorithm can be the cost effective solution. GPU can process large volume data in parallel when working in single instruction multiple data (SIMD) mode. In November 2006, the Compute Unified Device Architecture (CUDA) which is specialized for compute intensive highly parallel computation is unveiled by NVIDIA [6]. The NVIDIA CUDA Fast Fourier Transform library (cuFFT) provides a simple interface for computing FFTs up to 10x faster. By using hundreds of processor cores inside NVIDIA GPUs, cuFFT delivers the floating‐point performance of a GPU without having to develop your own custom GPU FFT implementation. cuFFT uses algorithms based on the wellknown Cooley-Tukey and Bluestein algorithms, so you can be confident that you’re getting accurate results faster than ever [8].

II. RELATED WORK
First let's discuss some libraries and frameworks that perform arbitrary precision arithmetic and in particular - big integer multiplication. System.Numerics.BigInteger [9] was introduced by Microsoft in .NET 4.0 and is the .NET type for large integers. The BigInteger type is an immutable type that represents an arbitrarily large integer whose value in theory has no upper or lower bounds. The members of the BigInteger type closely parallel those of other integral types. Because the BigInteger type is immutable (see Mutability and the BigInteger Structure) and because it has no upper or lower bounds, an OutOfMemoryException can be thrown for any operation that causes a BigInteger value to grow too large. One of them is IntX [10]. IntX is an arbitrary precision integers library with fast multiplication of big integers using Fast Hartley Transform. The GNU MP Library [11] - one of the fastest well-known Bignum libraries in the world. GNU MP (or GMP) is written in plain C and Assembly language so it compiles into optimized native code, it also uses fast calculation algorithms - that's why it's very fast. GMP is a free library for arbitrary precision arithmetic, operating on signed integers, rational numbers, and floating-point numbers. There is no practical limit to the precision except the ones implied by the available memory in the machine GMP runs on. Among other multiplication algorithms, GMP also uses FFT multiplication (depending on operand size). In [12] implemented FFT multiplication algorithm and done experiments by comparing FFT multiplications with normal multiplications at various bases. Also there is an existing large number multiplication implementation on CUDA by K. Zhao [13], where implemented multipleprecision Karatsuba and Montgomery multiplication algorithms.

III. THE DISCRETE FOURIER TRANSFORM
The one dimension of discrete Fourier transform (DFT of an N-point discrete-time signal f(x) is given by the equation:
image (1)
for u = 0, 1, 2, . . . , N − 1.
Similarly, for given F(u) we can obtain the original discrete function f(x) by inverse DFT:
image (2)
for x = 0, 1, 2, . . . , N − 1.
The Discrete Fourier Transform is frequently evaluated for each data sample, and can be regarded as extracting particular frequency components from a signal.

IV. THE FAST FOURIER TRANSFORM
The straightforward method of computing F on an element of cn takes O(n2) operations. However, there are algorithms for computing F in O(nlogn) steps. Let’s compute the Fourier transform of z = (z1, ..., z2n ). Let F2n denote the Fourier transform relative to C2n and let Fn denote the Fourier transform relative to Cn . Define
image (3)
Let [x]k denote the kth coordinate of a vector X. We have
image (4)
We define
image (5)
Here ZE and Zo are the vectors made respectively from the even and odd components of Z.With this notation, Equation 4 can be written more succinctly as follows.
image (6)
Equation 6 holds for all k = 0,...,2n-1, but we only need compute Ek and Ok for k=0,...,n-1 because
image (7)
Suppose it takes T(n) operations to compute the Fourier transform of a vector in Cn . The trick above shows that we can compute the Fourier transform of a vector in C2n using 2T(n)+8n. Here is a breakdown of the computation.
• We can compute {Ok} and {Ek} for k=0,...,n-1 in 2T(n) steps.
• We can compute ω2nk for k=0,...,2n-1 in 2n steps.
• It takes 3 more steps to compute each instance of Equation 6. So, this is a total of 6n additional steps.
We clearly have T(2°) ≤ 8. An easy induction argument shows
image (8)
This shows that, for n =2k the Fourier transform of a vector in Cn can be computed in O(n log (n)) steps. It is worth mentioning that “step” here refers to operations that are more complicated than simple floating point operations. For instance, a typical step involves multiplying a complex number of size log (n) with an nth root of unity. An actual analysis of the number of floating point operations needed to compute the Fourier transform would depend on how efficiently these individual steps could be done.

V. GPU ARCHITECTURE AND CUDA FFT (CUFFT) LIBRARY
GPUs are massively multithreaded manycore chips. NVIDIA Tesla products have up to 128 scalar processors, over 12,000 concurrent threads in flight, over 470 GFLOPS sustained performance. NVidia graphics card architecture consists of a number of so-called streaming multiprocessors (SM). Each one includes 8 shader processor (SP) cores, a local memory shared by all SP, 16384 registers, and fast ALU units for hardware acceleration of transcendental functions. A global memory is shared by all SMs and provides capacity up to 4 GB and memory bandwidth up to 144 GB/s. FERMI architecture introduces new SMs equipped with 32 SPs and 32768 registers, improved ALU units for fast double precision floating point performance, and L1 cache [14].
CUDA is a scalable parallel programming model and a software environment for parallel computing. It is very easy to use for programmer introduces a small number of extensions to C language, in order to provide parallel execution. Another important features are flexibility of data structures, explicit access on the different physical memory levels of the GPU, and a good framework for programmers including a compiler, CUDA Software Development Kit (CUDA SDK), a debugger, a profiler, and cuFFT and cuBLAS scientific libraries. The GPU executes instructions in a SIMT (single-instruction, multiple-thread) fashion. The execution of a typical CUDA program is illustrated in Fig. 1.
cuFFT key features are [8]
• 1D, 2D, 3D transforms of complex and real data types
• 1D transform sizes up to 128 million elements
• Flexible data layouts by allowing arbitrary strides between individual elements and array dimensions
• FFT algorithms based on Cooley-Tukey and Bluestein
• Familiar API similar to FFTW Advanced Interface
• Streamed asynchronous execution
• Single and double precision transforms
• Batch execution for doing multiple transforms
• In-place and out-of-place transforms
• Flexible input & output data layouts, similar tp FFTW "Advanced Interface"
• Thread-safe & callable from multiple host threads

VI. CUDA FFT BIG INTEGER MULTIPLICATION ALGORITHM
We now present the algorithm to multiply big integers with cuFFT. The basic idea is to use fast polynomial multiplication to perform fast integer multiplication. Fig. 2. shows the flow diagram of cuFFT multiplication algorithm. Let’s discuss every point of this diagram step by step.
(Color coding: white - host code, yellow - memory copy operation, green - device code)
1. Input values (a and b) can be given to program input in different ways. We can read them from a file or a database, or we can set them from the program interface. In our case user can insert input values from interface, but for testing and experimental purposes we have an option to generate random big integers. For number generation we use number of digits, which sets by the user.
2. For multiplication with FFT first we have to represent an integer as a polynomial. The default notation for a polynomial is its coefficient form. A polynomial p represented in coefficient form is described by its coefficient vector a = {a0, a1...,an-1} as follows:
image (9)
We call xthe base of the polynomial, and p(x) is the evaluation of the polynomial, defined by its coefficient vector a, for base x. Multiplying two polynomials results in a third polynomial, and this process is called vector convolution. As with multiplying integers, vector convolution takes O(n2) time. But convolution becomes multiplication under the discrete Fourier transform (convolution in time domain can be achieved using multiplications in frequency domain):
F(c) = F(a) F(b)
c = F-1 (F(a) F(b))
When we represent an integer as a polynomial, we have a choice in what base to use. Any positive integer can be used as a base, but for the sake of simplicity we restrict ourselves to choosing a base 10. Consider the integer 12345, whose polynomial form using base = 10 is a = {5, 4, 3, 2, 1}. Since FFT works with complex numbers, we have to get vectors of complex numbers. For this purpose, by setting imaginary part to zero, we get a = {[5, 0], [4, 0], [3, 0], [2, 0], [1, 0]} vector.
3. Determination of blockSize and gridSize of CUDA kernel. We done experiments to find the best block size for CUDA kernel, and grid size we calculate based on block size.
4. These transfers are the slowest portion of data movement involved in any aspect of GPU computing. The actual transfer speed (bandwidth) is dependent on the type of hardware you’re using, but regardless of this point, it is still the slowest. The peak theoretical bandwidth between device memory and the device processor is significantly higher than the peak theoretical bandwidth between the host memory and device memory. Therefore, in order to get the most bang for your buck in our application, we really need to minimize these host-device data transfers. If you have multiple transfers occurring throughout your application, try reducing this number and observe the results. In our case we have two “Copy data from host to device” operation:
cudaMemcpy(dev_a, a, numBytes, cudaMemcpyHostToDevice);
cudaMemcpy(dev_b, b, numBytes, cudaMemcpyHostToDevice);
5. Here we perform two forward FFTs for arrayA and arrayB. Result polynomial of multiplication arrayA and arrayB, arrayC has degree of two times greater than highest of degree arrayA and arrayB. So degree arrayC will be computed as:
signalSize = 2(a.Length > b.Length? a.Length : b.Length )
Before performing forward Fourier transform, we are padding the coefficients of arrayA and arrayB with zeros up to signalSize. We execute cuFFT plan with signalSize and cufftype.c2c.
6. At this point we have two transferred arrays on device, and we have to perform pairwise multiplication. Because we deal with complex data, we have:
Complex c;
c.x = a.x * b.x - a.y * b.y;
c.y = a.x * b.x + a.y * b.y;
7. Here we perform inverse FFT for arrayC
8. The formula for the transform that cuFFT uses is non-orthogonal by a factor of sqrt(signalSize). Normalizing by signalSize and 1/signalSize is what is needed when using FFTs to compute Fourier Series coefficients, so we divide result of point 7 to signalSize on device.
9. This point is similar to point 4, only here we copy memory back from device to host
10. Carry-propagation is the last step to get resulting polynomial. We will present pseudocode for this operation:
Pseudocode 1. Carry-propagation for big integer multiplication
Input: Integer array sourceArray
Output: Integer array resultArray
1. CarryPropagation()
2. carry := 0
3. for (i from 0 to sourceArray.length)
4. sum := carry + sourceArray[i]
5. mod := sum % 10
6. resultArray.Add(mod)
7. carry := sums / 10
8. end for
9. while (carry > 0)
10. if (carry.length > 1)
11. index := carry.length - 1
12. else
13. index := 0
14. end
15. resultArray.Add(carry[index])
16. carry := carry / 10
17. end while
11. In last step we form integer representation from polynomial and send result to output.

VII. EXPERIMENTS AND RESULTS
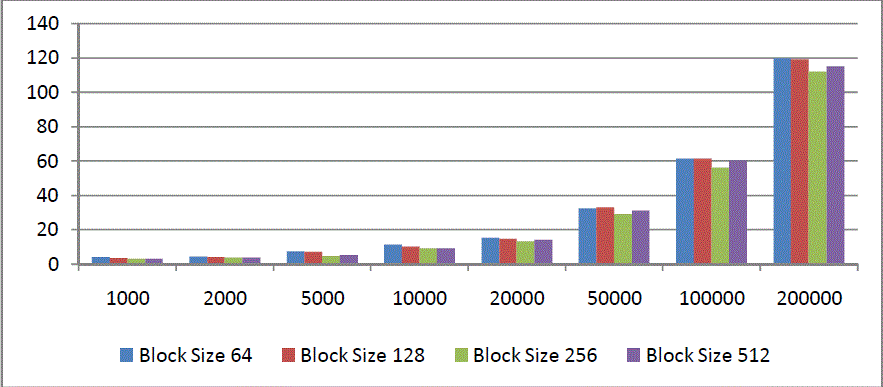
We have realized in CUDA 5.5 cuFFT multiplication algorithm, and conducted a series of benchmarks using a GeForce GT 630 graphics card on a desktop with the processor Intel(R) Core(TM) i3-2100 3.10GHz and 4 GB main memory. This graphics card has the compute capability 2.1, consists of 96 CUDA for integer and single-precision floating point arithmetic operations. We first vary the block size and calculate grid size based on block size to find their effect on the performance. Big integers are generated randomly in the test. We generate integers with different number of digits. In Table 1 presented block size effect on performance. We calculate time takes for one multiplication operation in milliseconds. We take average value for each data size after doing 100 test multiplication operations. Time for big integer generation is not taken into account in calculations.
Fig. 3. shows the diagram of experiment results shown in Table 1. As we can see, we have a best performance of multiplication, when block size of kernel is 256. We calculate grid size with following formula
gridSize = vectorSize/ blockSize + (vectorSize % blockSize ! = 0 ? 1: 0)
where vectorSize is the length of multiplying polynomials, “/” and “%” are div and mod operations respectively. Horizontal axis of Fig. 3 presents the number of digits of multiplied integers and vertical axis is time of multiplication in milliseconds. Block size determines the number of threads that can be executed in parallel within a single block. Maximum value for block size is based on GPU. We can have maximum 512 threads per block for GPUs with Compute Capability 1.x and 1024 threads per block for GPUs with Compute Capability 2.x and 3.x.
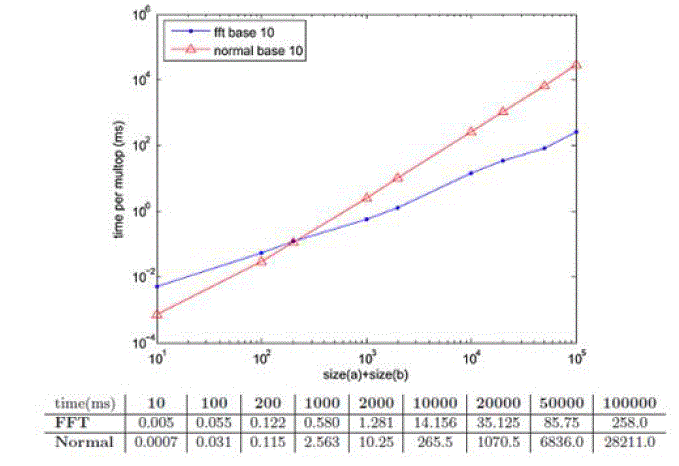
In his paper Ando Emerencia presents FFT multiplication algorithm and its comparison with normal multiplication, at various bases [12]. In Fig. 4 presented results from [12] for base 10. We will discuss base 10, because our experiments also are done for base 10. The individual values of the measurements taken are also listed in the table below. We see here that for an input size of more than 200, the FFT method becomes increasingly faster than normal multiplication. For an input size of 105, the FFT multiplication algorithm takes 258ms, while normal multiplication requires more than 28 seconds, so the time required differs by a ratio of more than a hundred.
We see here that for an input size of more than 200, the FFT method becomes increasingly faster than normal multiplication. For an input size of 105, the FFT multiplication algorithm takes 258ms, while normal multiplication requires more than 28 seconds, so the time required differs by a ratio of more than a hundred. If we compare Fig. 4 and Fig. 3, we can see that cuFFT multiplication is much times faster, about 5x faster for input size of 105.
Arbitrary-precision arithmetic in most computer software is implemented by calling an external library that provides data types and subroutines to store numbers with the requested precision and to perform computations. Different libraries have different ways of representing arbitrary-precision numbers. There are many arbitrary-precision arithmetic libraries which perform big integer multiplication. We choose three of them to run our experiments:
• Microsoft .net System.Numerics.BigInteger [9]
• IntX [10]
• GNU MP (or GMP) [11]
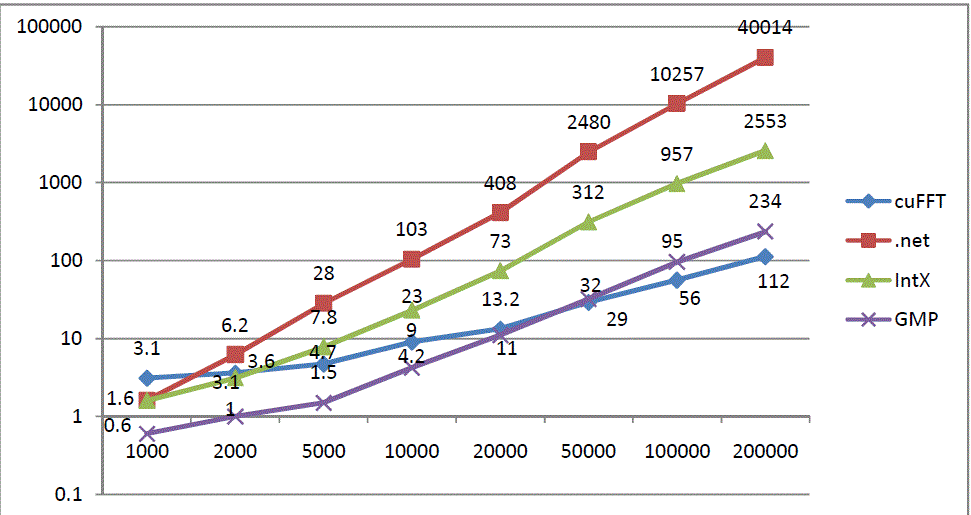
In Table 2 presented comparison of cuFFT multiplication with multiplications of .net BigInteger, IntX and GMP libraries. Experiments done for different sizes of input integer (number of digits). Provided experimental results are time for one multiplication operation in milliseconds. We have done 100 multiplication for each data size and library, and take average result. Fig. 5 is the chart representation of Table 2.
As we can see from this figure, for integers with 5000 digits, cuFFT is faster than .net BigInteger and IntX, but GMP is the fastest. cuFFT becomes faster than GMP starting from integers with 50000 digits. For data size 105. cuFFT is about 2 times faster than GMP.

VIII. CONCLUSION
As we can see, we gain in performance using parallel GPU based multiplication algorithm, with cuFFT library from CUDA. Experiments showed, that cuFFT multiplication is becoming faster than all other tested methods, when we deal with about 215 digit integers.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
 

References