International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Black Out Recovery in Transmission Network Using Greedy Algorithm

Naveen.G, Arther Jain .A
 M.E [Power Electronics and Drives], Thangavelu Engineering College,Chennai, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

A graph theory based methodology called dijkstra’s algorithm is used to find the energizing path of power to flow for a given network after a complete blackout is proposed here. Whenever a blackout occurs in the transmission network, the power system operators are under immense pressure to restore the network.The main aim of the power system restoration is to restore as much load as possible & as quickly as possible. After a blackout occurs first all the generators has to be energized and then synchronized. After synchronization of generators only all the loads can be supplied. For energizing the generators a sequential procedure has to be followed. If the sequence used is wrong then it may lead to cascaded outages.The Dijkstra's algorithm helps in finding the sequence to energize the generators based on least impedance path called minimum spanning tree. Newton Raphson based load flow technique is applied to this resultant minimum spanning tree(power flow path). Based on the results (voltage, current and power flow) obtained from the load flow solutions, other constraints of the restoration problem are applied.

Keywords
Graph theory, blackout, minimum spanning tree, load flow solution.

INTRODUCTION
Power system is a complex network involving the flow of power, which is generated using various techniques to meet the need of the industries or domestic consumers [1]. A brownout is an intentional drop in voltage in an electrical power supply system used for load reduction in an emergency [7]. A voltage reduction may be an effect of disruption of an electrical grid, or may occasionally be imposed in an effort to reduce load and prevent a blackout [9].

LOAD FLOW ANALYSIS
Power flow studies are of great importance in planning & designing the future expansion of power system as well as in determining the best operation of existing systems [2]. The principle information obtained from power flow study is the magnitude & phase angle of voltage at each bus the real & reactive power following in each line [3]. Power flow calculations usually employ iterative techniques such as Newton-Raphson method solves the polar form of power flow equations until P & Q mismatches at all buses fall within specified tolerances [8]. Newton’s method is a successive approximation procedure based on initial estimate of the unknown and the use of Taylor’s series expansion and the terms are limited to first order approximation [4]. LF Newton is developed for solution of power flow problems by Newton Raphson method [5].

GRAPH THEORY
Graph theory is a branch of data structures concerned about how the networks can be encoded & their properties measured [6]. A graph (G) is a set of points called vertices & the lines connecting the points called Edges. The graphs are broadly classified into two typesIt differs from a directed graph as each edge in E is an unordered pair of vertices. If (v,w) is an undirected edge then (v,w) = (w,v). The other classification is weighted & unweighted graphs. Here electrical network is analyzed as an undirected & weighted graph.

DIJKSTRA’S ALGORITHM
Dijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree [6]. It can also be used for finding costs of shortest paths from a single vertex to a single destination vertex by stopping the algorithm once the shortest path to the destination vertex has been determined.
By applying Dijkstra’s Algorithm we get minimum spanning tree of distance 0.83.

RECOVERY PROCESS
The whole recovery process is divided into 3 stages.

A. Black Start
Due to any critical fault or transient in the network a complete blackout will be occurring.

B. System Reconstruction
The generator (Slack bus) started first & based on the sequence of starting & starting time the generators on the network are started.

C. Load Recovery
Initially the critical loads are fed & later after stabilization of the critical loads all other loads are connected.
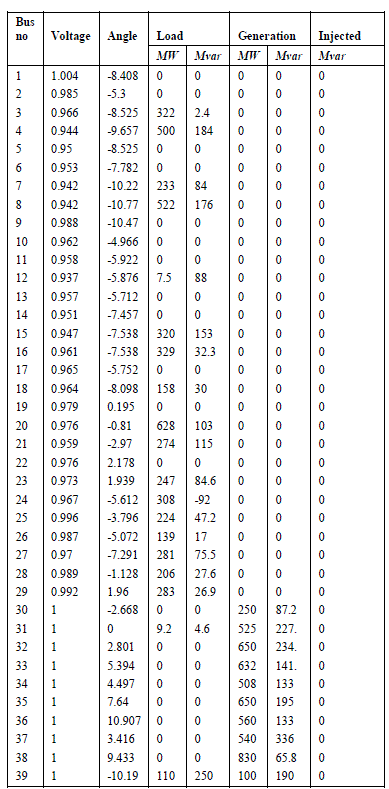
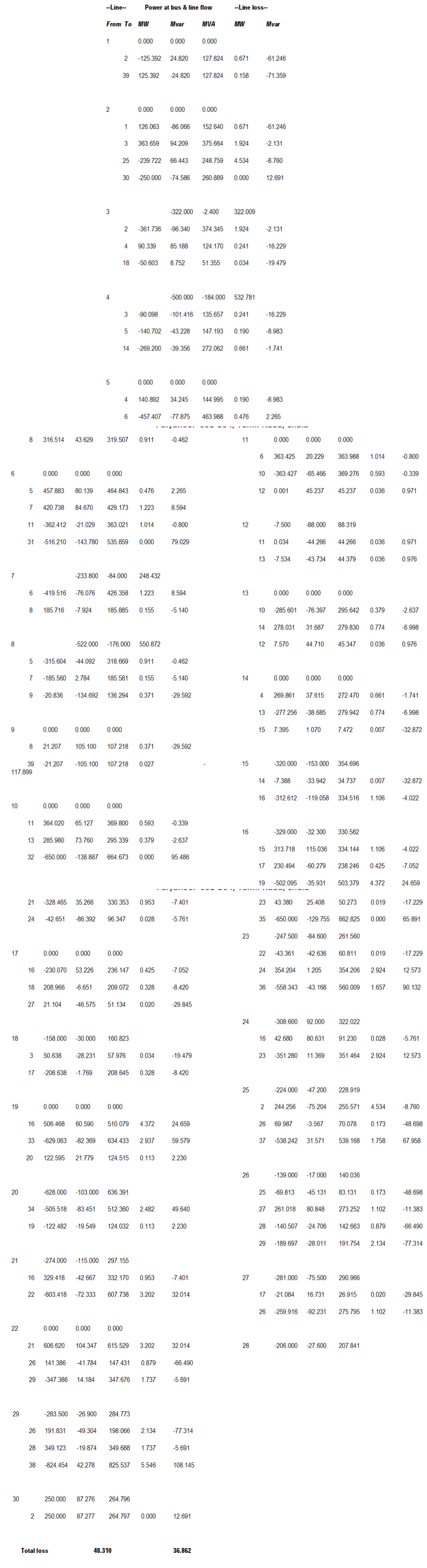
image

RESULTS OF NEWTON-RAPHSON METHOD
image

CONCLUSION
This paper presents the use of Dijkstra’s Algorithm for service restoration plan after a complete blackoutBy application of graph theory the process had been made simple and user friendly. In order to demonstrate the efficiency of dijkstra’s algorithm it has been applied to IEEE 10 Generator 39 Bus System. We carry out three stages of recovery process by using dijkstra’s algorithm. Newton-Raphson method is used to carry out load flow analysis. The simulation results show that Newton- Raphson method is effective and promising. It has been found that by application of dijkstra’s algorithm the transmission losses can be reduced to significant extent.The advantages are (1) solution procedure leads to the optimum solution & (2) avoid combinational explosion of the number of the number of configurations to be tested. This it is believed that the results from Dijkstra’s algorithm in power system restoration results in better plan, so it can be considered for real time application.Since the simulation implementation is done only for 39 bus system it can be extended to networks with more number of buses.

Tables at a glance
Table icon Table icon Table icon Table icon
Table 1 Table 2 Table 3 Table 4
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
 

References
  1. M.M. Adibi, R.J. Kafka, and D.P. Milanicz, “Expert System Requirements For Power System Restoration,” IEEE Transactions on Power Systems, vol. 9, no. 3, pp. 1592– 1598, 1994..
  2. M.M. Adibi, P. Clelland, and L. Fink et al., “Power System Restoration- A Task Force Report,” IEEE Transactions on Power Systems, vol. 2, no. 2, pp. 271–277, 1987.
  3. M.M. Adibi, J.N. Borkoski, and R.J. Kafka, “Power System Restoration -- The Second Task Force Report,” IEEE Transactions on Power Systems, vol. 2, no. 4, pp. 927–933, 1987.
  4. M.M.Abidi & R.J.Kafka, Power System Restoration Issues, 1990 .
  5. M.M.Abidi, L.H Fink “Power System Restoration Planning” IEEE transaction on Power Systems Vol-9, PP 22-28, February.
  6. Mark Allen Weiss (2007) Data Structures and Algorithm Analysis in c.
  7. “Development of an Interactive rule based system for bulk power system restoration ”,C.Y.Teo & Weishen,IEEE transaction on Power System, Vol-15, Num-2, May 2000
  8. J.Gutierrez et al.: Policies for Restoration of a Power System; IEEETRANS. v.PWRS-2 n.2, May 1987, pp.436-42.
  9. Hadi Saadat (1999) “Power System Analysis” McGraw-Hill, Newyork.