Efficient Feature Subset Selection Techniques
for High Dimensional Data

Sherin Mary Varghese; M.N.Sushmitha

Efficient Feature Subset Selection Techniques for High Dimensional Data

Sherin Mary Varghese¹ and M.N.Sushmitha²

M.Tech Student, Department of CSE, Hindustan University, Chennai, India
Assistant Professor , Department of CSE, Hindustan University, Chennai , India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

A database can contain several dimensions or attributes. Many Clustering methods are designed for clustering low–dimensional data. In high dimensional space finding clusters of data objects is challenging due to the curse of dimensionality. When the dimensionality increases, data in the irrelevant dimensions may produce much noise and mask the real clusters to be discovered. To deal with these problems, an efficient feature subset selection technique for high dimensional data has been proposed. Feature subset selection reduces the data size by removing irrelevant or redundant attributes. This algorithm works in two different steps that is minimum spanning tree based clustering methods and representative feature cluster selection. The proposed Pearson correlation measure focused on minimized redundant data. As a result, only a small number of discriminative features are selected.

Keywords

Feature subset selection, filter method, feature clustering, graph-based clustering, correlation analysis

INTRODUCTION

In machine learning and statistics, feature selection, also known as attribute selection, is the process of selecting a subset of relevant features for use in model construction. Feature selection has been an active and field of research and development for decades in statistical pattern recognition, machine learning, data mining and statistics. It has proven in both theory and practice effective in enhancing learning efficiency, increasing predictive accuracy, and reducing complexity of learned results[13]. The central assumption when using a feature selection technique is that the data contains many redundant or irrelevant features. Redundant features are those which provide no more information than the currently selected features, and irrelevant features provide no useful information in any context. Feature selection techniques are a subset of the more general field of feature extraction. Feature extraction creates new features from functions of the original features[12], whereas feature selection returns a subset of the features.

In the presence of hundreds or thousands of features, researchers notice that it is common that a large number of features are not informative because they are either irrelevant or redundant with respect to the class concept. In other words, learning can be achieved more efficiently and effectively with just relevant and non-redundant features. However, the number of possible feature subsets grows exponentially with the increase of dimensionality. F_inding an optimal subset is usually intractable and many problems related to feature selection have been shown to be NP-hard. Feature selection techniques are often used in domains where there are many features and comparatively few samples (or data points). The archetypal case is the use of feature selection in analysing DNA microarrays, where there are many thousands of features, and a few tens to hundreds of samples[11]. Feature selection is also useful as part of the data analysis process, as shows which features are important for prediction, and how these features are related. Irrelevant features, along with redundant features, severely affect the accuracy of the learning machines. Thus, feature subset selection should be able to identify and remove as much of the irrelevant and redundant information as possible. Many feature subset selection methods have been proposed and studied for machine learning applications. Existing feature selection approaches generally belong to the following two categories: wrapper and filter. Wrappers include the target classifier as a part of their performance evaluation, while filters employ evaluation functions independent from the target classifier. Since wrappers train a classifier to evaluate each feature subset, they are much more computationally intensive than filters. Hence, filters are more practical than wrappers in high-dimensional feature spaces. Their computational complexity is low, but the accuracy of the learning algorithms is not guaranteed.

In cluster analysis, graph-theoretic methods have been well studied and used in many applications. Their results have, sometimes, the best agreement with human performance. The general graph-theoretic clustering is simple: compute a neighbourhood graph of instances, then delete any edge in the graph that is much longer/shorter (according to some criterion) than its neighbours[12]. The result is a forest and each tree in the forest represents a cluster. Here, minimum spanning tree based clustering algorithms is used because they do not assume that data points are grouped around centres or separated by a regular geometric curve and have been widely used in practice. Based on the MST method, a Fast clustering bAsed feature Selection algoriThm (FAST) is proposed. The FAST algorithm works in two steps. In the first step, features are divided into clusters by using graph-theoretic clustering methods. In the second step, the most representative feature that is strongly related to target classes is selected from each cluster to form the final subset of features.

RELATED WORK

In [8] authors introduced a novel concept, predominant correlation, and propose a fast filter method which can identify relevant features as well as redundancy among relevant features without pair wise correlation analysis. The efficiency and effectiveness of our method is demonstrated through extensive comparisons with other methods using real-world data of high dimensionality. In [9] authors present a novel concept predominant correlation and propose a new algorithm that can effectively select good features based on correlation analysis with less than quadratic time complexity. A correlation based measure used in this approach. Two approaches classical linear correlation and Information theory are used. The algorithm used is FCBF, Fast correlation based filter. In [10] authors introduced the importance of removing redundant genes in sample classification and pointed out the necessity of studying feature redundancy. And proposed a redundancy based filter method with two desirable properties. It does not require the selection of any threshold in determining feature relevance or redundancy and it combines sequential forward selection with elimination, which substantially reduces the number of feature pairs to be evaluated in redundancy analysis. In [7] authors proposed a new framework of efficient feature selection via relevance and redundancy analysis, and a correlation-based method which uses C-correlation for relevance analysis and both C- and F-correlations for redundancy analysis. A new feature selection algorithm is implemented and evaluated through extensive experiments comparing with three representative feature selection algorithms. The feature selection results are further verified by two different learning algorithms. In [5] authors present an integrated approach to intelligent feature selection. They introduce a unifying platform which serves an intermediate step toward building an integrated system for intelligent feature selection and illustrate the idea through a preliminary system based on research. The unifying platform is one necessary step toward building an integrated system for intelligent feature selection. The ultimate goal for intelligent feature selection is to create an integrated system that will automatically recommend the most suitable algorithm to the user while hiding all technical details irrelevant to an application. In [13] authors present an optimization tool for attribute selection. This paper formulates and validates a method for selecting optimal attribute subset based on correlation using Genetic algorithm, where genetic algorithm used as optimal search tool for selecting subset of attributes. Correlation between the attributes will decide the fitness of individual to take part in mating. F_itness function for GA is a simple function, which assigns a rank to individual attribute on the basis of correlation coefficients. Since strongly correlated attributes cannot be the part of DW together, only those attributes shall be fit to take part in the crossover operations that are having lower correlation coefficients. In [11] authors generalised the ensemble approach for feature selection. So that it can be used in conjunction with many subset evaluation techniques, and search algorithms. A recently developed heuristic algorithm harmony search is employed to demonstrate the approaches. The key advantage of FSE is that the performance of the feature selection procedure is no longer depended upon one selected subset, making this technique potentially more flexible and robust in dealing with high dimensional and large datasets. In [14] authors identify the problems associated with clustering of gene expression data, using traditional clustering methods, mainly due to the high dimensionality of the data involved. For this reason, subspace clustering techniques can be used to uncover the complex relationships found in data since they evaluate features only on a subset of the data. Differentiating between the nearest and the farthest neighbours becomes extremely difficult in high dimensional data spaces. Hence a thoughtful choice of the proximity measure has to be made to ensure the effectiveness of a clustering technique. In [12] authors proposed a framework for feature selection which avoids implicitly handling feature redundancy and turns to efficient elimination of redundant features via explicitly handling feature redundancy. This framework composed of two steps: analysis of relevance determines the subset of relevant features by removing irrelevant ones, and analysis of redundancy determines and eliminates redundant features from relevant ones and thus produces the final subset. A novel clustering based feature subset selection algorithm for high dimensional data.

PROPOSED SYSTEM

Feature selection involves identifying a subset of the most useful features that produces compatible results as the original entire set of features. This algorithm works in two steps. In the first step, features are divided into clusters by using graph-theoretic clustering methods and in the second step, the most representative feature that is strongly related to target classes is selected from each cluster to form a subset of features. Pearson correlation is used for improving the efficiency and accuracy.

Advantages

• Low Time Consuming process

• Effective search is achieved based on feature search.

• There should be no outliers in the data.

• Easy to cluster the values.

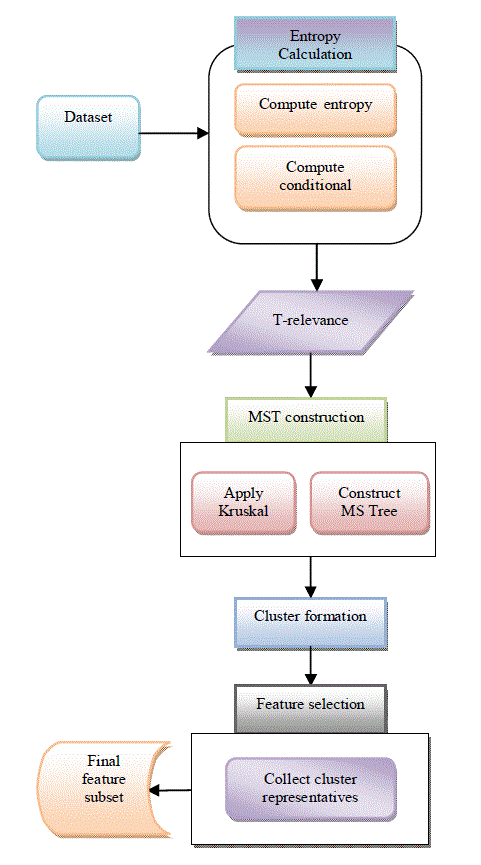
The proposed system has mainly six modules namely Load Data and Classify, Information Gain Computation, TRelevance Calculation, Pearson-Correlation Calculation, MST Construction, Cluster Formation. The data has to be preprocessed for removing missing values, noise and outliers. Then the given dataset must be converted into the arff format which is the standard format for WEKA toolkit. From the arff format, only the attributes and the values are extracted and stored into the database.

A. Information Gain computation

Relevant features have strong correlation with target concept so are always necessary for a best subset, while redundant features are not because their values are completely correlated with each other. Thus, notions of feature redundancy and feature relevance are normally in terms of feature correlation and feature-target concept correlation.

To find the relevance of each attribute with the class label, Information gain is computed. This is also said to be Mutual Information measure. Mutual information measures how much the distribution of the feature values and target classes differ from statistical independence. This is a nonlinear estimation of correlation between feature values or feature values and target classes.

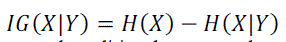To calculate gain, we need to find the entropy and conditional entropy values. The equations for that are given below:

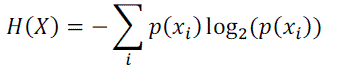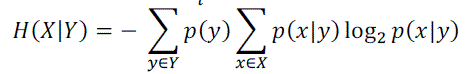Where p(x) is the probability density function and p(x|y) is the conditional probability density function.

B. T-relevance calculation and F-Correlation

The relevance between the feature F_i ∈ F and the target concept C is referred to as the T-Relevance of F_i and C, and denoted by SU (F_i,C). If SU (F_i,C) is greater than a predetermined threshold , we say that F_i is a strong T-Relevance feature.

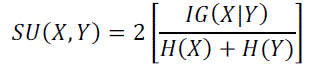After finding the relevance value, the redundant attributes will be removed with respect to the threshold value.The correlation between any pair of features F_i and F_j is called the F-Correlation of F_i and F_j, and denoted by SU(F_i ,F_j)

C. Pearson Correlation calculation

Pearson Coefficient is used to measure the strength of a linear association between two variables, where the value r = 1 means a perfect positive correlation and the value r = -1 means a perfect negative correlation.

D. MST Construction

Kruskal's algorithm is a greedy algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component).

The description is as follows

1. Create a forest F (a set of trees), where each vertex in the graph is a separate tree.

2. Create a set S containing all the edges in the graph

3. While S is nonempty and F is not yet spanning

a. remove an edge with minimum weight from S

b. if that edge connects two different trees, then add it to the forest, combining two trees into a single tree

c. Otherwise discard that edge.

At the termination of the algorithm, the forest forms a minimum spanning forest of the graph. If the graph is connected, the forest has a single component and forms a minimum spanning tree.

SYSTEM DESIGN AND IMPLEMENTATION

The proposed FAST algorithm logically consists of three steps:

(i) Remove irrelevant features,

(ii) Constructs a MST from relative ones,

(iii) Partitioning the MST and selects representative features

For the purposes of evaluating the performance and effectiveness of FAST algorithm, verifying whether or not the method is potentially useful in practice, and allowing other researchers to confirm our results, 35 publicly available data sets were used. The 35 data sets cover a range of application domains such as text, image and bio microarray data classification. A dataset file has been made in ASCII in CSV format, then conversion of this file to ARFF file is done. ARFF files are readable in Weka. The generated ARFF file is opened in Weka and then different processes like data cleaning, data processing and data transformation are applied on to the input database file. These steps act as preprocessing steps for the classification of data.

For a dataset D with m features and class C, T-Relevance is determined using the symmetrical uncertainty. Then Pearson correlation is used to reduce redundancy and construct a complete graph. The complete graph G reflects the correlations among all the target-relevant features. For high dimensional data, it is heavily dense and the edges with different weights are strongly interweaved. Moreover, the decomposition of complete graph is NP-hard. Thus for graph G, construct a MST, which connects all vertices such that the sum of the weights of the edges is the minimum, using the well known Kruskal’s algorithm. After building the MST, remove the edges, whose weights are smaller than both of the T-Relevance, from the MST and a Forest is obtained. Each tree in the Forest represents a cluster. Features in each cluster are redundant so choose some more features apart from the representative with the help of fixing the threshold and comprise the final feature subset.

RESULT AND ANALYSIS

When evaluating the performance of the feature subset selection algorithms, four metrics, 1) the proportion of selected features 2) the time to obtain the feature subset, 3) the classification accuracy, and 4) the Win/Draw/Loss record are used. The proportion of selected features is the ratio of the number of features selected by a feature selection algorithm to the original number of features of a dataset. The Win/Draw/Loss record presents three values on a given measure, i.e., the numbers of datasets for which our proposed algorithm FAST obtains better, equal, and worse performance than other five feature selection algorithms, respectively.

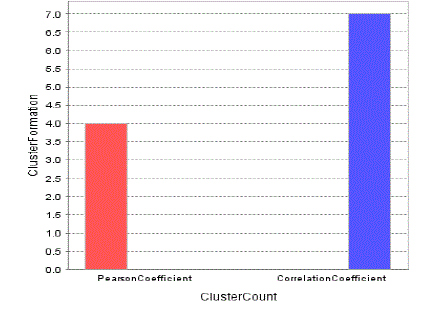
In the Existing System, there are so many clusters are formed based on the similar values. In this, we get accurate and small number of clusters. Through this, we can improve the efficiency by using Pearson coefficient.

CONCLUSION

In this paper, novel clustering- based feature subset selection algorithm for high dimensional data is presented. The algorithm involves removing the irrelevant features, constructs the minimum spanning tree from relative ones, and partitioning the MST and selects representative features. In the proposed algorithm, a cluster based feature selection is done and thus dimensionality is drastically reduced. For efficiency Pearson correlation is used for removing the redundant data. For the future work, we plan to explore different types of correlation measures.

ACKNOWLEDGEMENT

Authors would like to thank Department of CSE, Hindustan University for their valuable help and support.

Figures at a glance


Figure 1	Figure 2

References

Butterworth R., Piatetsky-Shapiro G.andSimovici D.A., ”On Feature Selection through Clustering”, In Proceedings of the Fifth IEEE international Conference on Data Mining, pp 581-584, 2005.

Das S., Filters, “wrappers and a boosting-based hybrid for feature Selection”, In Proceedings of the Eighteenth International Conference on Machine Learning, pp 74-81,2001

Demsar J., “Statistical comparison of classifiers over multiple data sets”, Journal of machine learning, 7, pp 1-30, 2006.

Forman G., “An extensive empirical study of feature selection metrics for text classification”, Journal of Machine Learning Research, 3, pp 1289-1305,2003

Huan Liu, “Toward Integrating Feature Selection Algorithms for Classification and Clustering”, IEEE transactions on knowledge and data engineering, VOL. 17, NO. 4, April 2005.
Krier C, Francois D, Rossi F and Verleysen M, “Feature clustering and mutual information for the selection of variables in spectral data”, In Proc

European Symposium on Artificial Neural Networks Advances in Computational Intelligence and Learning, pp 157-162,2007.

Lei Yu, Huan Liu, “Efficient Feature Selection via Analysis of Relevance and Redundancy”, Journal of Machine Learning Research, 5, 1205–1224,2004.

Lei Yu, Huan Liu,” Efficiently Handling Feature Redundancy in High Dimensional Data”, ACM, August 27, 2003.

Lei Yu, Huan Liu, “Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution”, Proceedings of the Twentieth International Conference on Machine Learning, 2003.

Lei Yu, Huan Liu,” Redundancy Based Feature Selection for Microarray Data”, ACM, August 2004.

QiangShen, RenDiao and Pan Su, “Feature Selection Ensemble”, Turing-100, vol.10, pp. 289–306, 2012

Qinbao Song, Jingjie Ni and Guangtao Wang, “A Fast Clustering-Based Feature Subset Selection Algorithm for High Dimensional Data”, IEEEtransactions on knowledge and data engineering, VOL:25, NO:1, 2013.

RajdevTiwari, Manu Pratap Singh, “Correlation-based Attribute Selection using Genetic Algorithm”, International Journal of Computer Applications, Volume 4– No.8, 0975 – 8887, August 2010.

SajidNagi, Jugal K, Dhruba K. Bhattacharyya, Kalita, “A Preview on Subspace Clustering of High Dimensional Data”, International journal ofcomputers & technology, Vol 6, No 3, May 2013.