In this paper, we present a new efficient distributed arithmetic (NEDA) formulation of the computation of 1-D discrete wavelet transform (DWT) using 9/7 filters, and mapped that into bit parallel for high-speed and low hardware implementations, respectively. We demonstrate that NEDA is a very efficient architecture with adders as the main component and free of ROM, multiplication, and subtraction. The bit-parallel structure has 100% hardware utilization efficiency. Compared with the existing multiplier-less structures, the proposed structures offer significantly higher throughput rate and involve less area-delay product.
Keywords |
| Discrete Wavelet Transform (DWT), NEDA, Xilinx Simulation. |
INTRODUCTION |
| The discrete wavelet transform (DWT) has been widely used in many areas of science and engineering, e.g., signal and
image processing, bio-informatics, geophysics, and meteorology etc. for the applications involving compression and
analysis of various forms of data. The well-known image coding standards, namely, MPEG-4 and JPEG2000 have adopted
DWT as the transform coder due to its remarkable advantages over the other transforms. For loss compression, Daubechies
9/7 orthogonal filter is used as the default wavelet filter in JPEG 2000. Efficient implementation of DWT using 9/7 filters
in resource-constrained hand-held devices with capability for real-time processing of the computation-intensive multimedia
applications is, therefore, a necessary challenge. Multiplier-less hardware implementation approach provides a kind of
solution to this problem due to its scope for lower hardware-complexity and higher throughput of computation. |
| Several designs have been proposed for the multiplier-less implementation of DWT based on the principle of distributed
arithmetic (DA) [1]–[5]. The structure of [1] and [2] distributes the bits of the fixed coefficients instead of the bits of input
samples. Consequently, the adder-complexity of the structure of [1] and [2] depends on the DA-matrix of the fixed
coefficients. |
| Martina et al [4] have approximated the 9/7 filter coefficients and expressed the 9/7 filter outputs in terms of 5/3 filter
outputs. By that approach, they have significantly reduced the adder-complexity of the 9/7 DWT. Longa et al [5] have
suggested an LUT-less DA-based design for the implementation of 1-D DWT. They have eliminated the ROM cells
required by the DA-based structures at the cost of additional adders and multiplexors. The adder-complexity of this
structure is significantly higher than the other multiplier-less structures.
In this paper, we have proposed an efficient scheme to derive NEDA-based bit-parallel structures, for low-hardware and
high-speed computation DWT using 9/7 filters. The remainder of the paper is organized as follows: mathematical
formulation of NEDA-based computation of DWT using 9/7 filter is presented in Section II. The proposed structures are
presented in Section III. Hardware and time complexity of the proposed structures are discussed and compared with the
existing structures in Section IV. Conclusion is presented in Section V. |
MATHEMATICAL DERIVATION OF NEDA |
| Let us consider the following sum of products: |
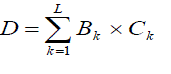 (1) (1) |
| Where k B are fixed coefficients and they k C are the input data words. Equation (1) can also be written in the form of a
matrix product as: |
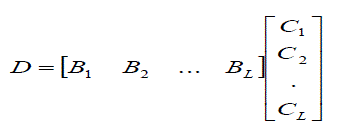 (2) (2) |
| Both k B and k C are in two’s complement format. The two’s complement representation of k B may be expressed as |
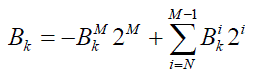 (3) (3) |
| Where i
k B 0 or 1, and i N, N+1… M and M
k B is the sign bit and N
k B is the least significant bit (LSB). |
| Equation (3) can be expressed in matrix form as: |
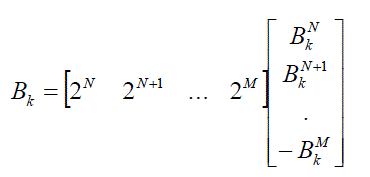 (4) (4) |
| Similarly k C can be represented in two’s complemented format as: |
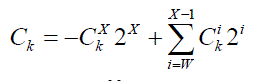 (5) (5) |
| Where i
k C 0 or 1, and i W, W+1, …,X and M
k C is the sign bit and N
k C is the least significant bit (LSB). |
| Now on combining equations (1) and (3), we get- |
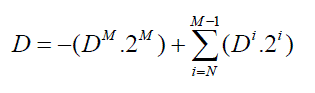 (6) (6) |
Where 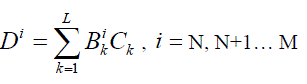 |
PROPOSED ARCHITECTURE |
| In this paper, we have proposed a multiplier-less architecture for 9/7 wavelet Filter by using NEDA. The filter coefficients
of 9/7 wavelet filter are given in table1. We multiply the filter coefficients by 100 for simplification. The mathematical
calculation for high pass output is explained by an example. |
| IN Table I, where h(0), h(1),… h(4) are the Low pass filter coefficients and g(0),g(1)…g(3) are the High pass filter
coefficients. |
| If we take the high pass coefficients g(0),g(1),g(2) and g(3), and multiply by r(1),r(2),r(3) and r(4) then we get the High
pass output H Y of the 9/7 filter as: |
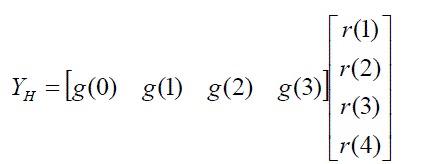 |
| Where r(1)=x(1)+x(n-6), r(2)=x(n-1)+x(n-5), r(3)=x(n-2)+x(n-4),r(4)=x(n-3).
Let r(1)=1, r(2)=2,r(3)=3,r(4)=4 then |
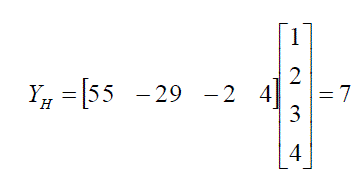 |
Now if we implement this with NEDA then 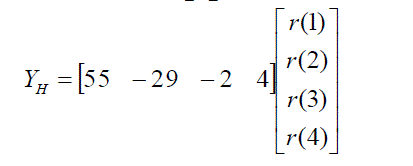 |
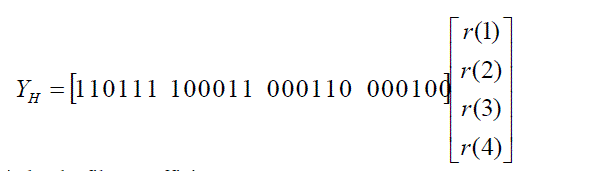 |
| Now we can make the DA matrix by the filter coefficients as |
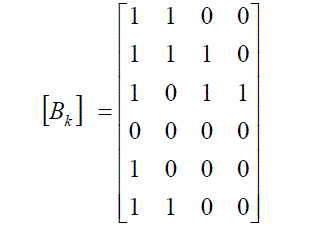 |
| And thus |
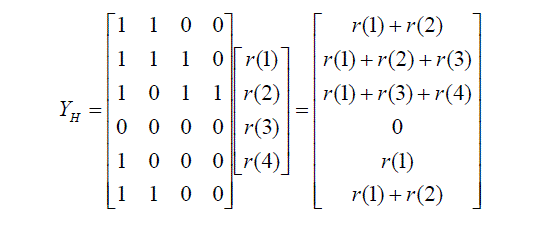 |
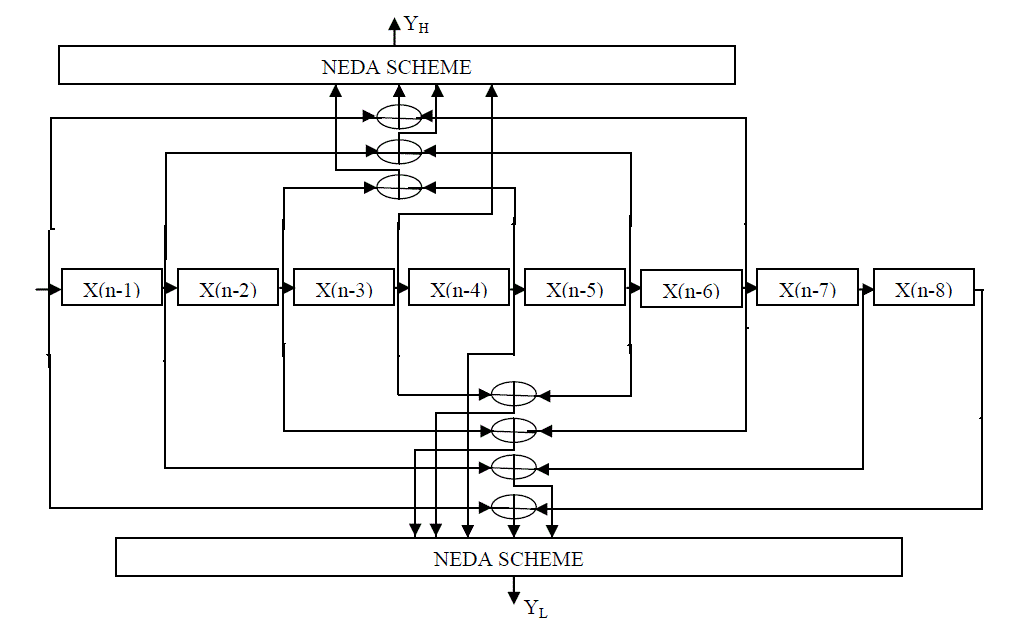
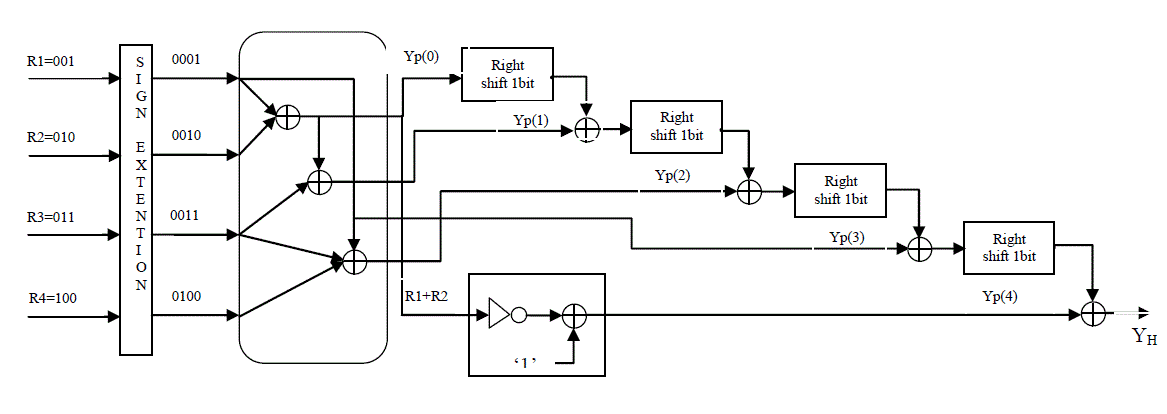
| Following the NEDA architecture in Fig. 1, the configuration for computing H Y is illustrated in Fig. 2. As can be observed
from this example, NEDA eliminates totally the encoder logic required in Booth Multiplier for two’s complement
manipulation. Furthermore, only one type of operations-addition, take place during the intermediate stages of computation,
greatly simplifying hardware design. What needs special care is the sign output from the adder array, which is simply
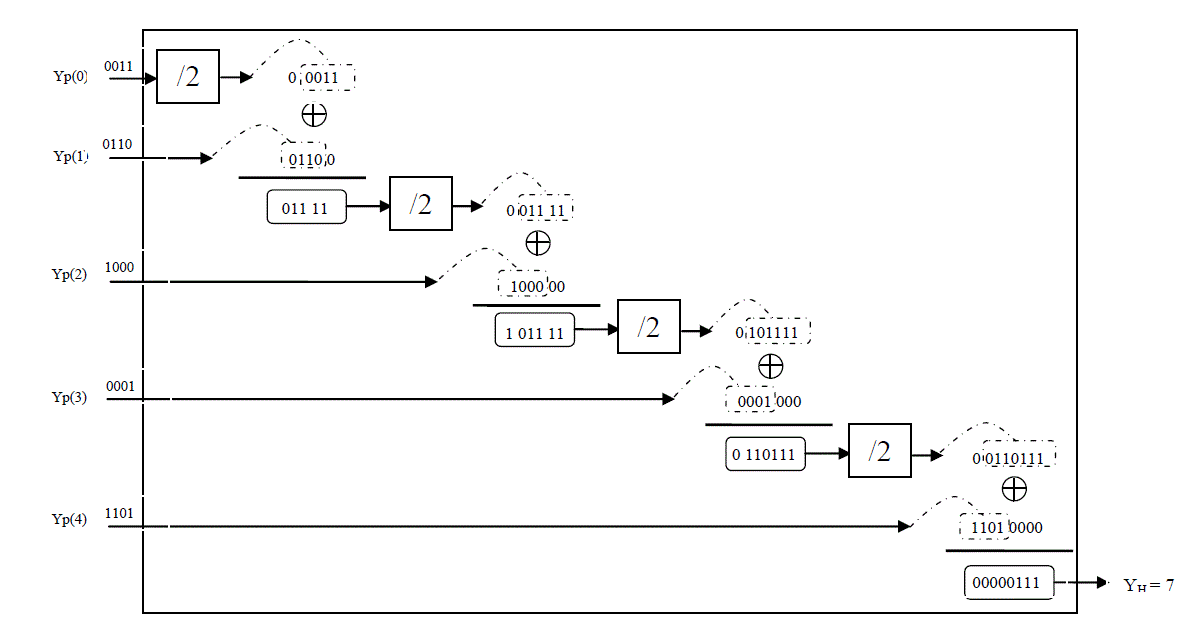
taking two’s complement. In the above example, invert-and-add-1 is all one needs to convert “0011” to “1101= P4 |
| The proposed architecture has very low hardware complexity compared to DA based structures, because DA requires ROM. In the proposed architecture, calculate the high-pass and low-pass wavelet filter output using NEDA scheme. NEDA does not require ROM. Proposed structure consists only 29 adders, zero mux and 27 registers. In the proposed architecture is better than other architecture in shown the table 2. Implementation the Longa et al. [5] and proposed architecture has been captured by VHDL and the functionality is verified by RTL and gate level simulation. To estimate the timing, area and power information for ASIC design, we have used Synopsys Design Compiler to synthesize the design into gate Level. Comparison of Synopsys result in the DA based architecture and NEHA based architecture is given in Table 3. |
CONCLUSION |
| We propose a novel distributed arithmetic paradigm named NEDA for VLSI implementation of DSP algorithms involving inner product of vectors. Mathematical proof is given for the validity of the NEDA scheme. We demonstrate that NEDA is a very efficient architecture with adders as the main component and free of ROM, multiplication, and subtraction. For the adder array, a systematic approach is introduced to remove the potential redundancy so that minimum additions are necessary. NEDA is an accuracy preserving scheme and capable of maintaining a satisfactory performance even at low DA precision. |
| In this paper, architecture suitable for high speed on-line applications. With this architecture the speed of the 9/7 wavelet filter transform is increased, occupied area of the circuit is reduced about 20-25% in the previous DA based architecture and reduced the power about 15-20% in the previous DA based architecture. It has 100% hardware utilization efficiency. |
Tables at a glance |
|
|
| |
Figures at a glance |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References |
- M. Alam, C. A. Rahman, and G. Jullian, ”Efficient distributed arithmetic based DWT architectures for multimedia applications,” in Proc. IEEE Workshop on SoC for real-time applications, pp. 333 336, 2003.
- X. Cao, Q. Xie, C. Peng, Q. Wang and D. Yu, ”An efficient VLSI implementation of distributed architecture for DWT,” in Proc. IEEE Workshop on Multimedia and Signal Process., pp. 364-367, 2006.
- M. Martina, and G. Masera, ”Low-complexity, efficient 9/7 wavelet filters VLSI implementation,” IEEE Trans. on Circuits and Syst. II, Express Brief vol. 53, no. 11, pp. 1289-1293, Nov. 2006.
- M. Martina, and G. Masera, ”Multiplierless, folded 9/7-5/3 wavelet VLSI architecture,” IEEE Trans. on Circuits and syst. II, Express Brief vol. 54, no. 9, pp. 770-774, Sep.2007.
- P. Longa, A. Miri, and M. Bolic, ”Modified distributed arithmeticased architecture for discrete wavelet transforms,” Electronics Letters vol. 44, no. 4, Feb. 2008.
- A.M. Shams, A. Chidanandan, W.Pan and M. A. Bayoumi, “NEDA: A Low-Power High-Performance DCT Architecture,” IEEE Transactions on signal processing, vol. 54, no. 3, march 2006.
- ArchanaChidanandan and MagdyBayoumi, “AREA-EFFICIENT NEDA ARCHITECTURE FOR THE 1-D DCT/IDCT,”
|