Research & Reviews: Journal of Material Sciences
MenuISSN:2321-6212
ISSN:2321-6212
Anchal Debnath1, Debajyoti Bhattacharjee2, Chandan Debnath2,3*
1 Department of Electrical Engineering, IIT Madras, Madras, Tamilnadu, India
2 Department of Physics, Tripura University, Suryamaninagar, Tripura, India
3 Department of Physics, Ambedkar College, Fatikroy, Unakoti, Tripura, India
Received: 12-Feb-2024, Manuscript No. JOMS-24- 127386; Editor assigned: 15- Feb-2024, PreQC No. JOMS-24- 127386 (PQ); Reviewed: 29-Feb-2024, QC No. JOMS-24- 127386; Revised: 07-Mar-2024, Manuscript No. JOMS-24- 127386 (R); Published: 14-Mar-2024, DOI: 10.4172/2321-6212.12.1.001
Citation: Debnath A, et al. Generalized form of Vectorial Laws of Reflection and Refraction and Application to Meta Material. RRJ Mater Sci. 2024;12:001.
Copyright: © 2024 Debnath A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Research & Reviews: Journal of Material Sciences
This communication presents the generalized laws of reflection and refraction in vectorial form with simple derivation. A few relations related to reflection and refraction in vectorial form have been included. The photon theory as well as the principle of conservation of momentum has been used for the derivation of these vectorial laws of reflection and refraction. The application of these laws in metamaterial has been discussed.
Generalized laws; Reflection and refraction; Vector calculus; Momentum conservation; Metamaterial
Geometrical optics is the branch of optics which is characterized by the limiting case of wavelength of
light λ →0. In this approximation, the optical laws may be formulated in the Language of geometry [1].
Appropriate formulation of the laws of reflection and refraction is possible by considering the implications
of Maxwell’s equation when λ →0. Light rays have been defined as the orthogonal trajectories to the
geometrical wave fronts S(x,y,z)=constant, and in a homogeneous medium the light rays have the form of a straight lin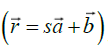e
where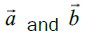
being a constant vector and s is a constant scalar [1]. This
equation is a vector equation of a straight line in the direction of the vector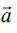 
passing through the point
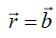Hence in a homogeneous medium, the light ray has the form of a straight line.
Born and Wolf in the year 1959, first mentioned the vectorial form of laws of refraction as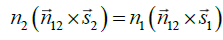 
[1]. In a slightly different form, Herzberger also wrote the laws of refraction in
vector form. After 46 years of Born and Wolf publication, P. R. Bhattacharjee, in the year 2005 first
lucidly explained the laws of reflection and refraction in vector form [2-5]. Subsequently, he published
many papers related to the vectorial representation of the laws of optics [6-15]. His publication rid the
ambiguity from the traditional exposition of laws of optics. In this communication, we have discussed the laws
of reflection and refraction in vectorial form in a slightly different way. We also included a few new relations related
to reflection and refraction in vectorial form. For the derivation of these vectorial laws of reflection and refraction,
we have used the photon theory as well as the principle of conservation of momentum.
Reflection-related laws in vector form
Traditional laws of reflection are i) The incident ray, the reflected ray and the normal at the point of incidence lie in the same plane. This plane is called the plane of incidence (or plane of reflection). ii) Angle of incidence is equal to the angle of reflection.
Now we explain these two laws in a generalized way in terms of vectors.
Incident ray, reflected ray and normal always lie in the same plane: We know that three vector lies in the same plane if the scalar triple vector of these vectors is zero. If we consider three vectors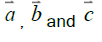
then they will lie in the same plane when
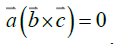So if we consider
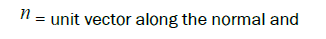
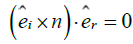
This relation represents that the incident ray, the reflected ray and the normal at the point of incidence lie in the same plane (Figure 1).
Figure 1: Diagram showing reflection of a ray of light by a plane mirror
Generalized form of the angle of incidence is equal to the angle of reflection: If we consider
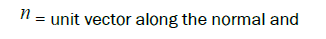
is a unit vector, which is normal to the plane in which incident ray, normal at the point of incidence and reflected
ray lie and in upward direction.
Here
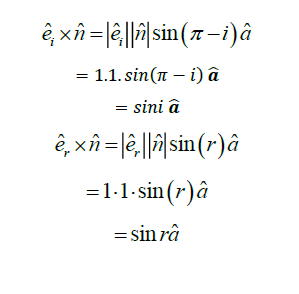
Now we use the concept of photon theory, according to which all photons of light of a particular frequency ν, have the same energy E (=hν), whatever the intensity of the radiation may be. By increasing the intensity of light of a given wavelength, there is only an increase in the number of photons per second crossing a given area, with each photon having the same energy. Thus, photon energy is independent of the intensity of radiation.
Again, we know that the frequency of radiation is independent of the medium so the energy of a photon is independent of the medium but the momentum of a photon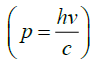
depends on the medium. In the case of
reflection, as incident and reflected ray lie in the same medium, so momentum remains same in case of incident
and reflected ray.
Using the conservation law of momentum of photon along the horizontal axis we get
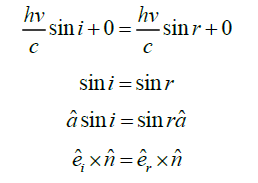
This relation represents the law of reflection in vector form (Figure 2).
Figure 2: Diagram showing unit vector incident ray and reflected ray with components along horizontal and vertical directions.
Direction of reflected ray in vector form: Vector form of reflected ray is;
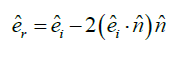
Let
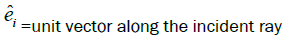
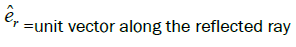
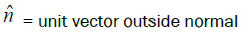
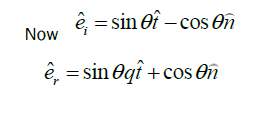
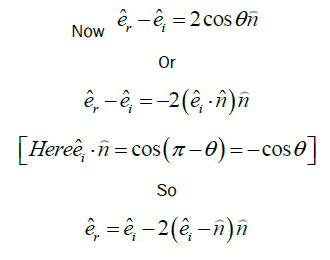
This relation helps to solve many problems related to reflection by a mirror. If light rays incident on a mirror
normally, then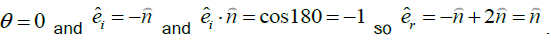 
So, we can easily conclude that if light ray’s incident on a mirror normally, it reflected back normally in opposite direction.
Laws of refraction in vector form in plane surface
Traditional laws of reflection are i) The incident ray, the refracted ray and the normal at the point of incidence lie in the same plane. This plane is called the plane of incidence (or plane of refraction). ii) Snell's law of refraction relates the sines of the angles of incidence and refraction at an interface between two optical media to the indexes of refraction of the two media: μ1 sin i =μ2 sinr , where μ1 and μ2 are the absolute index of refraction in the incident and in the refracting medium, respectively, while i and r are the angles of incidence and of refraction, respectively. while i and r are the angles of incidence and of refraction,
Now we explain these two laws in a generalized way in terms of vectors.
Incident ray, refracted ray and normal always lie in the same plane: We know that three vector lies in the same plane if the scalar triple vector of these vectors is zero. If we consider three vectors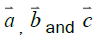 
then they will lay in the same plane when
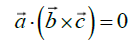
So if we consider
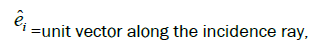
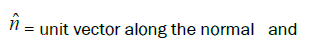
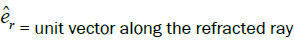
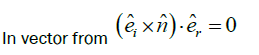
Snell’s law in generalised vector form: Snell's law describes the refraction of light as it passes through a boundary between two different media. In vector form, Snell's law relates the incident, refracted, and normal vectors at the interface, incorporating the refractive indices of the media involved. Using vector calculus, we derive Snell's law of refraction in vector form, which describes the change in direction and speed of light when it crosses the boundary between two different media. This representation is indispensable in various applications, such as designing lenses and analyzing light propagation through optical fibers etc. (Figure 3).
Figure 3: Diagram showing refraction with momentum of incident and refracted ray.
If we consider
is a unit vector, which is normal to the plane in which incident ray, normal at the point of incidence and refracted
ray lies and in upward direction.
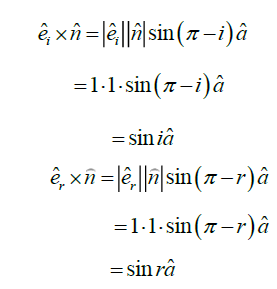
Here momentum of the photon in the first medium is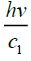
and in the second medium
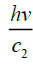[Here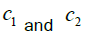
are velocities of light in the first medium and second medium respectively]. If μ1 is the absolute refractive index of the
first medium and μ2 is the absolute refractive index of the second medium, then using conservation law of
momentum of photon along horizontal direction we get (Figure 4).
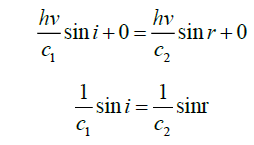
Multiplying both sides by c, we get
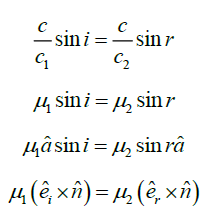
Applications in meta material
The phenomenon of negative refraction is an active area of contemporary research. Most materials have the absolute refractive index, μ >1. So, when a light ray from air enters a naturally occurring material, then by Snell’s law.
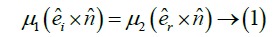
It is understood that the refracted ray bends towards the normal in the opposite side. But it never emerges on the same side of the normal as the incident ray. According to electromagnetism, the refractive index of the medium is given by the relation,
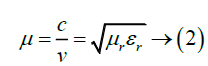
where c is the speed of the electromagnetic waves in vacuum, v its speed in the medium,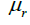 
is the relative permeability and
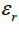is the relative permittivity.
Now for negative values of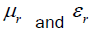 
we may write them as
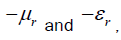then we may write:
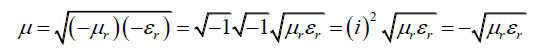
Such negative refractive index materials have now already been prepared artificially and are called meta-materials [16-19]. They exhibit significantly different optical behavior, without violating any physical laws. Since μ is negative, it results in a change in the direction of propagation of the refracted light. However, similar to normal materials, the frequency of light remains unchanged upon refraction even in meta-materials.
The left-hand side of equation (1) is always positive. Now for a meta-material if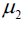 
is negative then the term
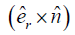in the right-hand side must be negative as the left-hand side is always positive. For right side to be negative, the angle between 
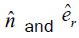must be greater than 1800 so the refracted rays must lie on the same side
to the normal as shown in Figure 4.
Figure 4: Diagram showing refraction in case of meta material.
This communication, from the view point of academic interest, will enhance the theoretical foundation of the generalized vectorial laws of reflection and refraction. At the same time, it will enrich the traditional laws of physics as well. For deriving these laws, simple formula of vector calculus and conservation of momentum were used