Grey Level X-ray Image De-noising Using
Singular Value Decomposition Method

Satish Kumar; R; hir Singh; Javid Khan

Grey Level X-ray Image De-noising Using Singular Value Decomposition Method

Satish Kumar¹, Randhir Singh², Javid Khan³

M.Tech, Department ECE, Shri Sai College of Engineering and Technology, Pathankot, India
HOD, Dept ECE, Shri Sai College of Engineering and Technology, Pathankot, India
Associate Analyst, Global Logic Technologies, Delhi, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Research work is carried out to investigate the effectiveness of the SVD based technique to filter biomedical images. Different noise level images were taken and the image quality parameters such as PSNR, SNR, RMSE, and MAE were calculated with respect to original image. After subjecting to the algorithm the image quality parameter were calculated and compared to the noisy images parameters. It is observed from that the algorithm works effectively to filter the noisy images.

Keywords

SVD, noise, PSNR, MAE.

INTRODUCTION

Image filtering techniques are needed nowadays due to the massive production of digital images and movies. Generally these techniques are required due to the fact that often digital images are taken in poor conditions. In-order to extend the range of action of a camera, an improvement in image is always desirable. A digital is generally represented as matrix of grey level or RGB colour values [1-4]. A digital image in case of grey level images, i is a point on a 2D grid and u(i) is a real value. Colour images have triplet values of u(i) for red, green, and blue components. Blur and noise are two limitations in image accuracy. Image with noise added to it can be represented as

v(i)= u(i) +n(i)

where v(i) is the observed value, u(i) is the true pixel value at i, and n(i) is the noise perturbation.

Image de-noising is the operation of removing unwanted noise from a noise-corrupted image, restoring the image to its un-degraded ideal. SVD technique is implemented to de-noise the biomedical images. SVD can be computed as

A=UΣV^T

U U and T V V yields the identity matrix. Hence U and V are matrix of orthonormal columns. ? matrix is a diagonal elements ? σ 1 2 3 , , ,...., . D ? ? ? ? The values of ? σ 1 D k k ? ? are called singular values and having a decreasing order i.e. 1 2 3 .... 0. D ? ?? ?? ? ?? ? SVD has a remarkable property of statistical representation of A in subspaces of decreasing importance. A can be reconstructed by setting all of the singular values to zero except 1 ? . The resulting matrix has a rank of one. Also it can be proven that AK, the rank-K approximation to A using only the first K singular values, is the closest rank-K matrix to A. After designing the algorithm images were subjected to evaluate the following image quality parameter described below

Root mean square error (RMSE) corresponds to pixels in the reference image and the fused image. If the reference image and fused image are alike give the RMSE value equal to zero and it will increase when the dissimilarity increases between the reference and fused image [10].

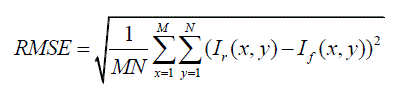Peak signal to noise ratio (PSNR) value will be high when the fused and reference images are alike and higher value implies better fusion. PSNR is calculated by follow equation [11-12]

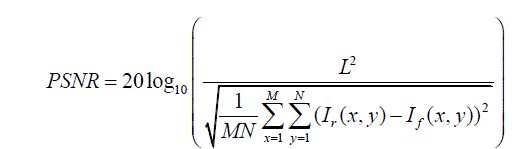Signal to noise ratio (SNR) is calculated using following [13]

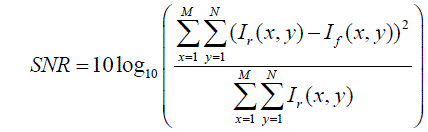METHODOLOGY`

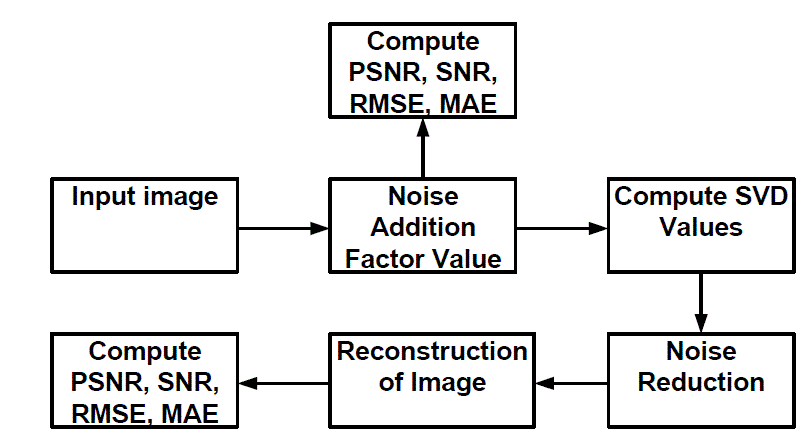
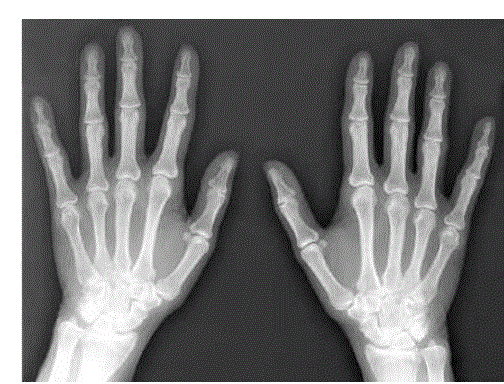
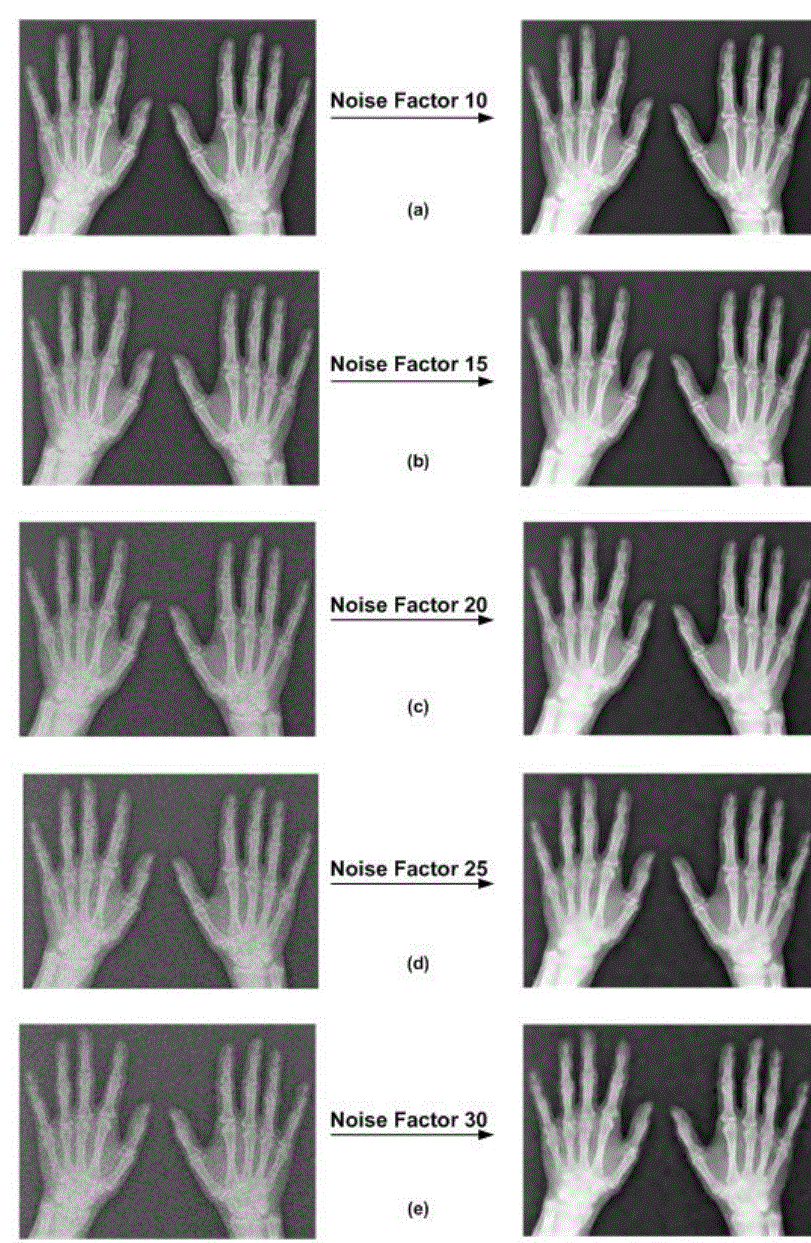
Research work is carried out design an algorithm based on SVD technique to de-noise the X-ray image of human hand. Figure 1 shows the block diagram of the schematic implemented to de-noise the image. An original input image in grey level was taken shown in Fig. 2. In order to obtain noisy image, a random signal with multiple of scalar quantity ranging from 10 to 30 with step size of 5 is added to the original image. The size of original image matrix and random noise signal matrix are of same size. After adding the noise in the image, various image quality parameter of the noisy image such as PSNR, SNR, RMSE, and MAE value were calculated with respect to original image. These values were kept for the comparative analysis between the noisy and filtered image. After subjecting the noisy image to the algorithm, the PSNR, SNR, RMSE, and MAE of the reconstructed image were calculated.

RESULT AND DISCUSSION

Computer based algorithm to filter the noisy image employing SVD technique has been designed. Figure 3 shows the noisy images with increasing order of the noise level factor in first column and corresponding de-noised images in second column. Computed values of PSNR, SNR, RMSE, and MAE for noisy images and de-noised images with respect to original image are given in TABLE I and TABLE II respectively.

CONCLUSION

Research work is carried out to design the computer based algorithm to filter noisy X-ray images. SVD based technique is implemented to filter the images. PSNR, SNR, RMSE, and MAE of the noisy image for lowest level are 27.42 dB, -0.00250 dB, 18.85, 19.84 and for highest level are 19.45, -0.00256, 47.21, 51.88 respectively. Similarly for de-noised image quality parameter for lowest level are 33.82 dB, -0.00342 dB, 9.02, 10.21 and for highest level are 30.53 dB, -0.00092 dB, 13.18, 13.18 respectively.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3

References

A. Buades, B. Coll, J.M. Morel (2005), „A review of image denoising algorithms, with a new one,? SIAM Journal on Multiscale Modeling and Simulation Vol. 4, pp. 490-530.

C. Shannon. and W. Weaver (1998), The mathematical theory of communication, University of Illinois Press,.

Jeff Orchard, Mehran Ebrahimi, Alexander Wong (2008), „Efficient nonlocal-means denoising using the SVD,? ICIP, pp. 1732-1735.

H. J. Seo, P. Chatterjee, H. Takeda, and P. Milanfar (2007), „A comparison of some state of the art image denoising methods,? Proceeding41st Asilomar Conference on Signals, Systems, and Computers.

Sandeep Arya, Saleem Khan, Dhrub Kumar, Maitreyee Dutta, ParveenLehana, “Image enhancement technique on Ultrasound Images using Aura Transformation,” International Journal in Foundations of Computer Science & Technology (IJFCST), vol.2, no.3, pp. 1-10, May 2012.

Sandeep Arya and ParveenLehana, Development of a Seed Analyzer using the Techniques of Computer Vision, International Journal of Distributed and Parallel Systems (IJDPS) Vol.3, pp. 149-155, 2012.

S.M. Smith and J.M. Brady (1997), „Susan - a new approach to low level image processing,? International Journal of Computer Vision, Vol. 23, pp. 45-78.

L.P. Yaroslavsky (1985), Digital Picture Processing-An Introduction, Springer Verlag.

S.J. Osher, A. Sole, and L.A. Vese (2003), „Image decomposition and restoration using total variation minimization and the h-1norm,? MultiscaleModeling and Simulation, Vol. 1, pp. 349-370.

R. Ashino, A. Morimoto, M. Nagase, R. Vaillancourt (2004), „Image compression with multiresolution singular value decomposition andother methods,?CRM-2939, ibid.

V. P. S. Naidu (2010), „Discrete Cosine Transform-based Image Fusion,?Def. Sci. J., Vol. 60, pp. 48-54.

R. A., Gonzalo (2005), Nonlinear Signal Processing – A statistical approach, Wiley-Interscience Inc., Publication, USA.

M. A. Mohamed, A. F I. A. Fattah, A. S. Asem, A. S. El-Bashbishy, (2011) “Medical image filtering, fusion and classification techniques,” Egyptian Journal of Bronchology, Vol. 5, pp. 142-151.