Keywords
|
| erasure code; key servers; distributed image storage system; re-encryption |
INTRODUCTION
|
| Cloud computing is a model for enabling convenient, on-demand network access to a shared pool of configurable computing resources (e.g., networks, servers, storage, applications, and services) that can be rapidly provisioned and released with minimal management effort or service provider interaction. As high-speed networks and ubiquitous Internet access become available in recent years, many services are provided on the Internet such that users can use them from anywhere at any time [1],[4],[6]. For enterprises, cloud computing is worthy of consideration and try to build business systems as a way for businesses in this way can undoubtedly bring about lower costs, higher profits and more choice; for large-scale industry. For instance, Russell Lands, recreational developer in Alabama – instead of investing in its own IT infrastructure, it turned to Connecteria Cloud Storage thereby saving $25000 to $35000. Users just use services without being concerned about how computation is done and storage is managed. A cloud storage system consists of many storage servers which can provide a long term information sharing service in Internet [7]. In this paper, we focus on designing a cloud storage system for robustness, confidentiality, and functionality for storing biomedical images. |
| However, security concerns become relevant as we now outsource the storage of possibly sensitive data to third parties [5], [8]. In this paper, we are particularly interested in the following security issues. First, we need to provide guarantees of access control, in which we must ensure that only authorized parties, can access the outsourced data on the cloud [9]. Secondly, we must prohibit third-party cloud storage providers from mining any sensitive information of their clients’ data for their own marketing purposes. |
| Cloud storage providers typically keep multiple backup copies of data for fault-tolerance reasons [5]. For providing robustness, cloud system is modelled as collection of storage servers. In order to provide strong confidentiality for biomedical images in storage servers, the data owner encrypts the images by a cryptographic method and the storage server encodes the encrypted images using d-dimensional erasure codes before storing them [2], [11]. |
| Upon data retrieval by the data owner or by any authorized user, he needs to retrieve the code word symbols from storage servers, decode them, and then decrypt them by using cryptographic keys. Therefore the user has to bear the computation and communication traffic between the storage server and himself. The user must also manage the cryptographic keys there by facing the issues caused when the key is compromised. Moreover when the data owner needs to forward the images to any other user (as the doctors across globe needs to share their patient data for better diagnosis & study), he has to retrieve, decode, decrypt and then forward them. In this paper, we address the problem of forwarding data to another user by storage servers directly under the request of the data owner. We also have key servers which manage the keys of data owners and it works independently with storage servers. |
A. Infrastructure of the Proposed System
|
| There are n distributed storage servers and m key servers in the cloud storage system. Any compressed medical image is divided into k blocks and represented as a vector of k symbols. Our contributions are as follows: |
| 1. We construct a secure cloud storage system that supports the function of secure image forwarding by using a n-server forward re-encryption scheme [10]. The encryption scheme supports decentralized d-dimensional erasure codes over encrypted images and forwarding is done upon demand by the image owner by storage server itself. Our system is highly distributed where storage servers independently encode and forward images and key servers independently perform partial decryption of images. |
| 2. We assume that the number of storage servers is much greater than number of blocks of an image.. The sacrifice is to slightly increase the total copies of an encrypted image symbol sent to storage servers. Nevertheless, the storage size in each storage server does not increase because each storage server stores an encoded result (a code word symbol), which is a combination of encrypted medical image. |
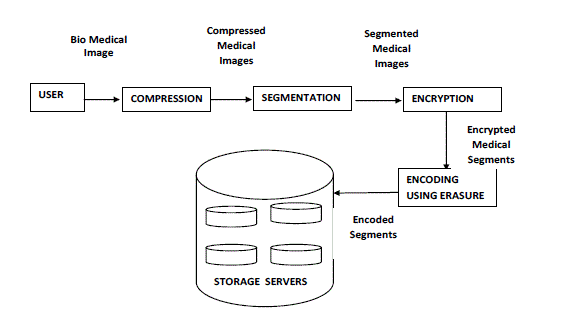
| The medical image is compressed, encrypted and then encoded as a code word, which is a vector of symbols, and each storage server stores a code word symbol. A storage server failure is modeled as a d-dimensional erasure error of the stored code word symbol. Random linear codes support distributed encoding, that is, each code word symbol is independently computed. To store a image of k blocks, each storage server linearly combines the blocks with randomly chosen coefficients and stores the code word symbol and coefficients. To retrieve the image, a user queries k storage servers for the stored code word symbols and coefficients and solves the linear system. |
II. RELATED WORK
|
| In [1] author has discussed the various issues regarding storage of medical images in a cloud. The major issue is the security concerned with preserving the privacy of the patient. Erasure codes can be used for encoding in a distributed system for fault tolerance is in [2].In [3] authors have discussed how medical images can be securely shared with other users. The authors [4] have discussed the trend in storing medical information in cloud due to its infrastructure facility. The file accessing mechanism proposed in [5] proposes the file system that is used for storing in the cloud. The distributed file storage system is fault tolerant in retrieval and forwarding. The de-centralized erasure code can be used for securely storing the information in a cloud is discussed by authors in [6]. [7] is an example of public cloud storage provided by amazon. The authors [8], [11] proposed algorithms for secure medical information sharing in a cloud environment. Distributed key management scheme reduces the burden of the users for storing the keys securely and encrypting the information discussed in [9]. The authors [10] propose the concept of re-encryption using public key of receiver and private key of sender when forwarding the information to a different user. The authors [12] discussed the secure storage of information in cloud. In [13] the inclusion of the key management layer in distributed environment is proposed. The authors [14] provide mechanism for secured authentication for storage and deletion. The authors [15] provide library for implementing the erasure code in c/c++. |
III. DISTRIBUTED IMAGE STORAGE SYSTEM
|
| Our system aims to achieve confidentiality through n-server forward re-encryption scheme and robustness by erasure codes. The overall design of the system is centered around two concepts double encryption on forwarding and erasure encoding. |
A. Architectural Design
|
| The architecture is decentralized, so storage systems offer good scalability, because a storage server can join or leave without control of a central authority. To provide robustness against server failures, a simple method is to make replicas of each image and store them in different servers. However, this method is expensive as z replicas result in z times of expansion. |
| Our paper proposes to control this expansion rate by using erasure code to encode the images. An encrypted form of compressed image is encoded as a code word which is vector of symbols and each storage server stores a code word symbol. A storage server failure is modelled as an erasure error of the stored code word symbol. Distributed encoding of image symbols is done with the help of random linear codes, that is, each code word symbol is independently computed. To store the image of k blocks, each storage server linearly combines the blocks with randomly chosen coefficients and stores the code word symbol and coefficients. To retrieve the image, a user queries k storage servers for the stored code word symbols and coefficients and solves the linear system. Consider the case that n=ak for a fixed constant a. Distributing each block of a image to v randomly chosen storage servers is enough to have a probability 1- k=p-o(1) of a successful data retrieval, where v = b ln k, b > 5a, and p is the order of the used group. The sparsity parameter v= b ln k is the number of storage servers which a block is sent to. The larger v is, the communication cost is higher and the successful retrieval probability is higher. The system has a light data confidentiality because an attacker can compromise k storage servers to get the image. |
B. n-Server Forward Re-encryption Scheme
|
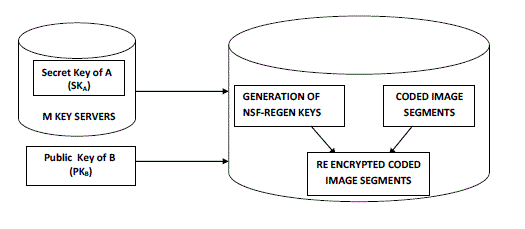
| This scheme is implemented in storage server. As described earlier, the storage server encodes the cipher before storing it. It can also transfer the cipher to any other user upon the request of the data owner. For example, if user A intends to transfer medical images to user B, A calculates a re- encryption key RKAB based on the public key of B - PKB and secret key of A – SKA and securely sends the re-encryption key to the storage server . Using RKAB, the storage servers re-encrypts the original code word symbols into re-encrypted code word symbols. The re-encrypted code word symbols can be later retrieved by B and is decryptable using B’s secret key [8],[10]. Thus the confidentiality and robustness is strengthened by double encryption and encoding. |
IV. DEPLOYMENT
|
| We describe our model of the proposed system and a risk model for evaluating confidentiality and robustness. |
| A. System Model |
| Our system model consists of users n storage servers SS1; SS2; . . . ; SSn, and m key servers KS1; KS2; . . . ; KSm. Storage servers provide storage services and key servers provide key management services. They work independently. Our distributed storage system consists of four phases as follows |
| 1. Initial association, Image storage, Image forwarding, and Image retrieval. These four phases are described as follows. In the initial association phase, the system manager chooses system parameters and publishes them. Each user A is assigned a public-secret key pair (PKA; SKA). User A distributes his secret key SKA to key servers such that each key server KSi holds a key share SKAi, 1<=i<=m. The key is shared with a threshold t [6], [9]. |
| 2. In the Image storage phase, user A encrypts his image M and dispatches it to storage servers. A image M is decomposed into k blocks m1;m2; . . .;mk and has an identifier ID. User A encrypts each block mi into a cipher text Ci and sends it to v randomly chosen storage servers. Upon receiving cipher texts from a user, each storage server linearly combines them with randomly chosen coefficients into a code word symbol and stores it. Figure 1 shows the block diagram of biomedical image storage. Note that a storage server may receive less than k image blocks and we assume that all storage servers know the value k in advance. |
| 3. In the Image forwarding phase, user A forwards his encrypted image with an identifier ID stored in storage servers to user B such that B can decrypt the forwarded image by his secret key. To do so, A uses his secret key SKA and B’s public key PKB to compute a re-encryption key RKAB and then sends RKAB to all storage servers. Each storage server uses the re-encryption key to re-encrypt its codeword symbol for later retrieval requests by B. Figure 2 given below shows the block diagram of image forwarding phase. The re-encrypted code word symbol is the combination of cipher texts under B’s public key. |
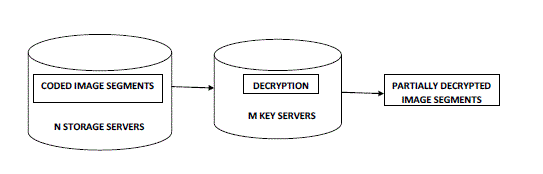
| 4. In the Image retrieval phase, user A requests to retrieve a medical image from storage servers. The medical image is either stored by him or forwarded to him. User A sends a retrieval request to key servers. Upon receiving the retrieval request and executing a proper authentication process with user A, each key server KSi requests u randomly chosen storage servers to get codeword symbols and does partial decryption on the received codeword symbols by using the key share SKAi. Figure 3 given below shows the block diagram of image retrieval phase. Finally, user A combines the partially decrypted codeword symbols to obtain the original image M. |
| B. Risk Model |
| We consider data confidentiality for both data storage and data forwarding. In this threat model, an attacker wants to break data confidentiality of a target user. To do so, the attacker colludes with all storage servers, non-target users, and up to (t-1) key servers. The attacker analyzes stored images in storage servers, the secret keys of non-target users, and the shared keys stored in key servers. Note that the storage servers store all re-encryption keys provided by users. The attacker may try to generate a new re-encryption key from stored re-encryption keys. |
| A cloud storage system modelled in the above is secure if no probabilistic polynomial time attacker wins the game with a non-negligible advantage. A secure cloud storage system implies that an unauthorized user or server cannot get the content of stored images, and a storage server cannot generate re-encryption keys by himself. If a storage server can generate a re-encryption key from the target user to another user B, the attacker can win the security game by reencrypting the cipher text to B and decrypting the re-encrypted cipher text using the secret key SKB. Therefore, this model addresses the security of data storage and data forwarding. |
C. Solution for Risk Evaluation
|
| A straightforward solution to supporting the image forwarding function in a distributed storage system is as follows: when the owner A wants to forward a image to user B, he downloads the encrypted image and decrypts it by using his secret key. He then encrypts the image by using B’s public key and uploads the new cipher text. When B wants to retrieve the forwarded image from A, he downloads the cipher text and decrypts it by his secret key. The whole data forwarding process needs three communication rounds for A’s downloading and uploading and B’s downloading. The communication cost is linear in the size of the forwarded image. The computation cost is the decryption and encryption for the owner A, and the decryption for user B. |
| n-server forward re-encryption schemes can significantly decrease communication and computation cost of the owner. In a n- server forward re-encryption schemes, the owner sends a re-encryption key to storage servers such that storage servers perform the re-encryption operation for him. Thus, the communication cost of the owner is independent of the size of forwarded image and the computation cost of re-encryption is taken care of by storage servers. n- server forward re-encryption schemes significantly reduce the overhead of the data forwarding function in a secure storage system. |
V. CONSTRUCTION OF SECURE MEDICAL IMAGE CLOUD STORAGE
|
A. Initial association
|
| The association algorithm generates the system parameters μ. A user uses KeyGen() to generate his public and secret key pair and ShareKeyGen() to share his secret key to a set of m key servers with a threshold t, where k <=t <=m. |
1. SetUp(). Run Gen() to obtain (g, h,e, G1, G2,p) where  is a bilinear map, g and h are generators of G1, and both G1 and G2 have the prime order p.. Set µ=(g, h,e, G1, G2,p) where f is a bilinear map, g and h are generators of G1, and both G1 and G2 have the prime order p.. Set µ=(g, h,e, G1, G2,p) where f is a one-way hash function. is a one-way hash function. |
| 2. KeyGen(): For a user A, the algorithm selectsa1; a2; a3 ?R Zp and sets PKA=(ga1,ha2) SKA=(a1, a2, a3). |
| 3. ShareKeyGen(SKA, t, m). This algorithm shares the secret key SKA of a user A to a set of m key servers by using two polynomials fA,1(z) and fA,2(z) of degree t-1 over the finite field GF(p). |
 |
 |
| where v,; v2, . . . ; vt ? R Zp. The key share of the secret key SKA to the key server KSi is SKA,i = (f A,1(i) ,f A,2(i)) where 1 ≤ i≤ m. |
B. Image storage
|
| When user A wants to store a image of k blocks m1,m2,….,mk with the identifier ID, he computes the identity token τ =hf(a3,ID)and performs the encryption algorithm Enc(.) on τ and k blocks to get k original ciphertexts C1, C2, . . . , Ck. An original cipher text is indicated by a leading bit b = 0. User A sends each cipher text Ci to v randomly chosen storage servers. A storage server receives a set of original cipher texts with the same identity token τ from A. When a ciphertext Ci is not received, the storage server inserts Ci =(0,1, τ ,1) to the set. The special format of (0,1, τ ,1) is a mark for the absence of Ci. The storage server performs Encode(.) on the set of k ciphertexts and stores the encoded result (codeword symbol). |
| 1. Enc(PKA, τ,m1,m2,…mk). For m1g1,i, this algorithm computes |
 |
| 2. Encode(C1, C2, . . . , Ck). For each ciphertext Ci, the algorithm randomly selects a coefficient gi. If some ciphertext Ci is (0,1, τ ,1) the coefficient gi is set to 0. Let Ci =(0,α i,β,γ i) The encoding process is tocompute an original codeword symbol Co |
 |
| Where |
 |
C. Image forwarding
|
| User A wants to forward a image to another user B. He needs the first component a1 of his secret key. If A does not possess a1, he queries key servers for key shares. When at least key servers respond, A recovers the first component a1 of the secret key SKA via the KeyRecover(.)algorithm. Let the identifier of the image be ID. User A computes the reencryption key RKID via the ReKeyGen(.) algorithm and securely sends the re-encryption key to each storage server. By using RKID a storage server re-encrypts the original codeword symbol C0 with the identifier ID into a re-encrypted codeword symbol C00 via the ReEnc(.) algorithm such that C00 is de-cryptable by using B’s secret key. A reencrypted codeword symbol is indicated by the leading bit b=1. Let the public key PKB of user B be(gb1,hb2). |
| 1. KeyRecover(SKA;i1,, SKA;,2 ; . . . ; SKA;it ). Let T ={ i1,i2,….,it} This algorithm recovers a1 via Lagrange interpolation as follows |
 |
| 2. ReKeyGen(PKA; SKA; ID;PKB). This algorithm selects e? R Z p*and computes |
 |
| 3. ReEnc(RKIDA->B; C0). Let C0= (0,α i,β,γ i) =(0,gτ’,τ,W?(ga1, gτ’,τ ) for some r’ and some W, and RKIDA->B= (h b2a1 (f(a3,ID)+e),ha1e) for some e. The re-encrypted codeword symbol is computed as follows |
 |
| Note that the leading bit 1 indicates C00 is a re-encrypted cipher text. |
| D. Image retrieval |
| There are two cases for the image retrieval phase. The first case is that a user A retrieves his own image. When user A wants to retrieve the image with the identifier ID, he informs all key servers with the identity token τ. A key server first retrieves original codeword symbols from u randomly chosen storage servers and then performs partial decryption ShareDec(.)on every retrieved original codeword symbol C0. The result of partial decryption is called a partially decrypted codeword symbol. The key server sends the partially decrypted codeword symbols ς and the coefficients to user A. After user A collects replies from at least t key servers and at least k of them are originally from distinct storage servers, he executes Combine(.) on the t partially decrypted code word symbols to recover the blocks m1;m2; . . .;mk. The second case is that a user B retrieves a image forwarded to him. User B informs all key servers directly. The collection and combining parts are the same as the first case except that key servers retrieve re-encrypted codeword symbols and perform partial decryption ShareDec(.) on re-encrypted codeword symbols. |
| 1. ShareDec(SKj;Xi). Xi is a codeword symbol, where Xi=(b,α,β,γ) and b is the indicator for original and reencrypted codeword symbols. SKj is a key share, where SKj =(sk0 sk1). By using the key share SKj, the partially decrypted codeword symbol ς i,j of Xi is generated as follows: |
 |
| 2. Combine In the first case b = 0 for original codeword symbols, user A wants to retrieve his own image. The algorithm combines the t values (βi1,j1,βi2,j2,…βit,jt) to obtain τa1=τ fA,1(0) via the Lagrange interpolation over exponents |
 |
| For each of the partially decrypted codeword symbols ς i,j where i ? SI, the algorithm computes |
 |
| for some r0, where fA,1(0)=a1. |
| Observe that wi=m1g1,i m2g2,i.. mkgk,i and there are k such equations. Consider the square matrix K=[g i,j] where 1 ≤ i≤ k, j ? Si . The decoding process is to compute K-1 and output the blocks m1,m2, . . .,mk. The algorithm fails when the square matrix K is noninvertible. In the second case b = 1 for re-encrypted codeword symbols, user B wants to retrieve the image forwarded to him. The algorithm does the following computation to obtain |
 |
| where fB,2(0)=b2 -1. Again, for each of τ i;j, where i ? SI, the algorithm computes an encoded block |
 |
| The rest in the second case is the same as that in the first case. |
VI. CONCLUSION
|
| We present a practical cloud storage system which aims to provide access control , robustness and confidentiality over medical images shared in al cloud storage system. We use n- server forward re-encryption scheme and ddimensional erasure codes for providing security. We describe the essential operations on cryptographic keys so as to achieve access control and authorized access. To decrypt a image of k blocks that are encrypted and encoded to n codeword symbols, each key server only has to partially decrypt two codeword symbols in our system. Storage servers provide the forwarding operation on authorized request without the participation of user and key servers manages the keys on behalf of user thereby reducing the user overhead. Moreover, each storage server independently performs encoding and re-encryption and each key server independently performs partial decryption. Medical Imaging and Cloud computing could become the most data and computing intensive activities in future. Cost effective measures which provide strong security for such data are essential. Therefore, we have presented a secure and cost effective biomedical image sharing in cloud storage systems. |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References
|
- Steve G. Langer (2010), “Challenges for Data Storage in Medical Imaging Research”, Journal of Digital Imaging, pp.203-207.
- James S. Plank, Mario Blaum, James L. Hafner (2012 ), “SD Codes: Erasure Codes Designed for How Storage Systems Really Fail”
- Technical Report UT-CS-12-701, EECS Department, University of Tennessee, November.
- Fatma E.-Z. A. Elgamal, Noha A. Hikal, F.E.Z. Abou-Chadi “Secure Medical Images Sharing over Cloud Computing environment” -
- (IJACSA) International Journal of Advanced Computer Science and Applications.
- Arnon Rosenthal , Peter Mork , Maya Hao Li , Jean Stanford , David Koester , Patti Reynolds (2010 ), “Cloud computing: A new businessparadigm for biomedical information sharingJournal of Biomedical Informatics, Volume 43, Issue 2, April, Pages 342–353.
- Chao-Tung Yang,Lung-TengChen,Wei-Li Chou(2010), “Implementation of a Medical Image file Accessing System on CloudComputing”, IEEE international Conference on Computational Science and Engineering,pages 321-326.
- Hsiao-Ying Lin, Wen-GueyTzeng,( 2010),.”A Secure Decentralized Erasure Code for Networked Storage Systems”, IEEE Transactionson Parallel and Distributed Systems, 21(11), pp.1586-1596.
- Amazon Elastic Compute Cloud(EC2), http://www.amazon.com/ec2.
- Zhuo-Rong Li, En-Chi Chang, Kuo-Hsuan Huang, Feipei Lai (2011), “A Secure Electronic Medical Record Sharing Mechanism in theCloud Computing Platform” IEEE 15th International Symposium on Consumer Electronics, pp. 450-457.
- Yi-Ruei Chen, Wen-GueyTzeng (2012), “Efficient and Provably-Secure Group Key Management Schemes Using Key Derivation”,11th IEEE International Conference on Trust, Security and Privacy in Computing and Communications (IEEE TrustCom-2012), June.
- G. Ateniese, K. Fu, M. Green, and S. Hohenberger (2006), “Improved Proxy Re-Encryption Schemes with Applications to SecureDistributed Storage”, ACM Trans. Information and System Security, vol. 9, no. 1, pp. 1-30.
- Jiang Bian, RemziSeker and UmitTopaloglu (2010), “A Secure Distributed File System for Medical Image Archiving”, IEEEInternational Conference on Social Computing, pages 961-967.
- Danwei Chen and Yanjun He (2010), "A Study on Secure Data Storage Strategy in Cloud Computing", Journal of ConvergenceInformation Technology, Volume 5, Number 7, September.
- K. Bowers, A. Juels, and A. Oprea( 2009), “Hail: A highavailability and integrity layer for cloud storage”, 16th ACM ConferenceonComputer and Communications Security.
- Yang Tang, Patrick P.C. Lee, John C.S. Lui, RadiaPerlman(2012), “Secure Overlay Cloud Storage with Access Control and AssuredDeletion” Ieee Transactions On Dependable And Secure Computing,Vol.9, No. 6, November/December.
- J. S. Plank, S. Simmerman, and C. D. Schuman. Jerasure(2008),” A library in C/C++ facilitating erasurecoding for storage applications -Version 1.2” Technical Report CS-08-627, University of Tennessee, August.
|