Keywords
|
| MAP Algorithm, Log MAP Algorithm, Jacobian logarithm, SB/DB and Log Likelihood ratio. |
INTRODUCTION
|
| The MAP algorithm which is used in the turbo decoders is operated in the logarithmic domain in order to reduce the computational complexity [1]. The computation of log likelihood ratio with the values of state metrics is more complicated with log exponential sum calculation. The log exponential sum can be simplified by Jacobian algorithm by adding a correction term along with the max operator. The correction function calculation is critical because of the performance and complexity of the turbo decoder. So a lot of methods [2][3][4] are used to simplify the computation to satisfy the performance requirements. |
| This paper proposes an algorithm to compute the correction function that will be used to calculate the state metrics and log likelihood values. Furthermore this Log Likelihood values can be modified into SB/DB mode with a new set of equations and this will increase the performance parameters of the Turbo decoders. |
| The rest of the paper is organized as follows: in section II, brief introduction and derivation of basic MAP and Log MAP algorithmic equations. Section III reviews different methods of approximation of the correction function. In Section IV, the SB/DB mode calculations are presented. Section V presents the results and discussions. This paper is finally concluded in the Section VI. |
DIFFERENT METHODS OF MAP ALGORITHM
|
| In this section different method of MAP algorithms were discussed. The mathematical equations required for the Log Map algorithm is introduced with a max operator and the Max Log Map algorithm is also presented. |
| A. DIGITAL COMMUNICATION SYSTEM MODEL. |
| A Digital communication system is represented by figure 1.Map algorithm for the block of binary data input sequence D=D1, D2….DN is represented in figure1. The encoder consists of two identical recursive systematic Convolutional encoders (RSC) with M memory elements. The code rate of the encoder is ½ with two outputs which is the sequence of Xs = Xs1, Xs2…XsN. and the parity bit sequence Xp = Xp1, Xp2…XpN. |
| The corresponding received sequence from the channel with the noise is Y=Ys, Yp which consist of pair of received systematic and parity bits. |
| B. MAXIMUM A POSTERIORI (MAP) ALGORITHM |
| The objective of the MAP algorithm is to calculate Log Likelihood Ratio (LLR) (Λ (Dk)) of the a posteriori probability (APP) of Dk = 1 to Dk = 0. The state of the encoder is represented by Sk at time k. The state transition is from k-1 to k. The LLR value can be given by equation 1. |
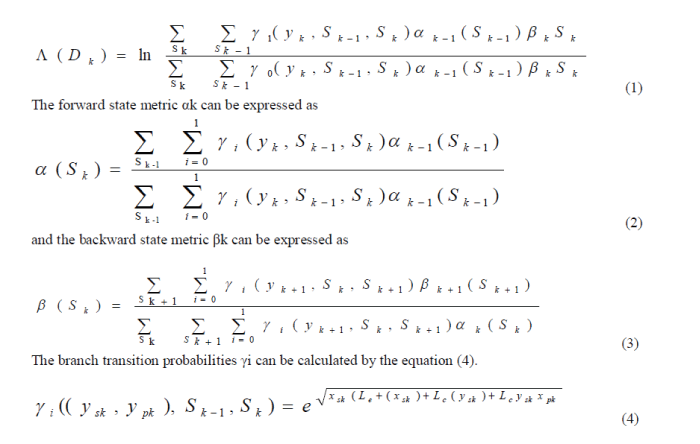 |
| The channel reliability value Lc = 2 / σ2 with σ2 is the noise variance and Le is the extrinsic information which gives a priori information. |
| C. LOG MAP ALGORITHM |
| The complexity in the MAP algorithm can be reduced by Log MAP algorithm. To avoid complicated calculations in the MAP algorithm, the entire MAP algorithm is calculated in Logarithmic domain. So the basic equations in the MAP algorithm (2), (3) and (4) are converted into log domain which reduces the number of multiplications and addition operations used. So,áüÃÆk(Sk) = ln αk(Sk). |
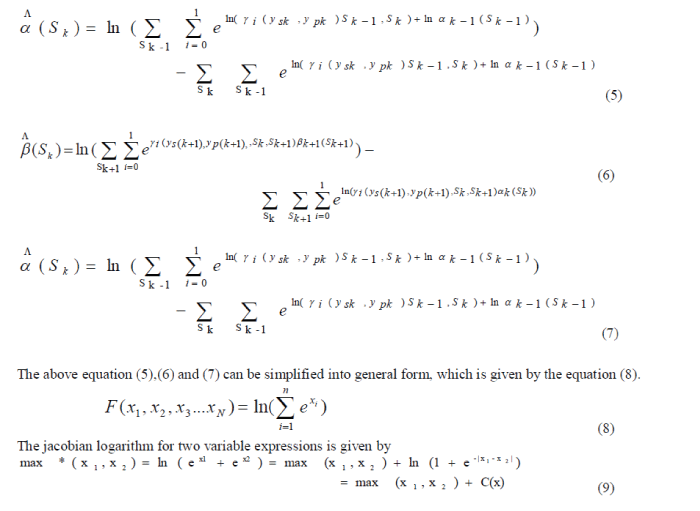 |
| The calculation of the correction term C(x) in (9) is more complicated in Log MAP algorithm. The same form of log exponential sum occurs in the calculation of backward state metrics(βk) , and LLR Λ (Dk).So, to improve the performance of the Log Map Algorithm, a simple method of implementation of correction function must be required. The easiest method of finding out the correction function is presented in [5].But this requires more memory to store the table sequences. A new method used in this calculation is presented in Section III. |
| D. MAX LOG MAP ALGORITHM |
| The max log map algorithm introduces an approximation max*(x1,x2) ≈ max (x1,x2 ). This Max log map algorithm simply omitting the correction term C(x).But the performance of the Log Map algorithm is dropped by 10% compared to Log Map algorithm. Even though the Max Log Map algorithm is least complex, it gives worst BER. So, in Max Log Map algorithm, a simple implementation of correction function is required to improve the performance of the turbo decoders. |
DIFFERENT ALGORITHMS FOR THE CALCULATION OF CORRECTION FUNCTION
|
| In this section a different methods of existing algorithms which are approximates the correction function are discussed. The performance tradeoff for adding the correction elements with these algorithms are also discussed. |
| In the Linear Log Map algorithm proposed in [6], the MacLaurin Series expansion is used and it is observed that the correction function is approximately zero. |
 |
| This method of correction is more accurate. This method of algorithm employs with shift registers storing the ln(2).For fast computation , a speed registers are required for this algorithm. Figure 2 shows the graphical comparison of various Approximations to the correction function. |
DUAL MODE SINGLE BINARY/DOUBLE BINARY (SB/DB) MAP DECODING
|
| The SB/DB Map decoding is introduced by Y.Sen [9] and C.Y Shen [10] for radix 4 Map architecture to achieve high hardware usage and shared storage information. In general, the MAP is composed of branch metrics, forward recursion state metrics, backward recursion state metrics, a priori LLR, a posteriori LLR, and extrinsic information. For the dualmode MAP decoding, the radix-4 SB MAP decoding and radix-4 DB MAP decoding are employed because of their computational similarity. So, the equations of branch metrics, forward state metrics, backward state metrics, a priori LLR, a posteriori LLR, and extrinsic information are reformulated for SB / DB Decoding. |
| A) RADIX-4 SB MAP DECODING |
| The arithmetic operations of the of the Radix-4 SB MAP are described as |
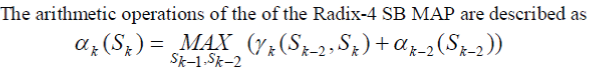 |
| m – number of parity bit and the sign bit of posteriori LLR value decides whether uk=0 or uk=1. |
| B) RADIX-4 DB MAP DECODING |
| In DB mode two binary bits are encoded uk= u1k,u2k. The arithmetic operations of the of the Radix-4 DB MAP are described as |
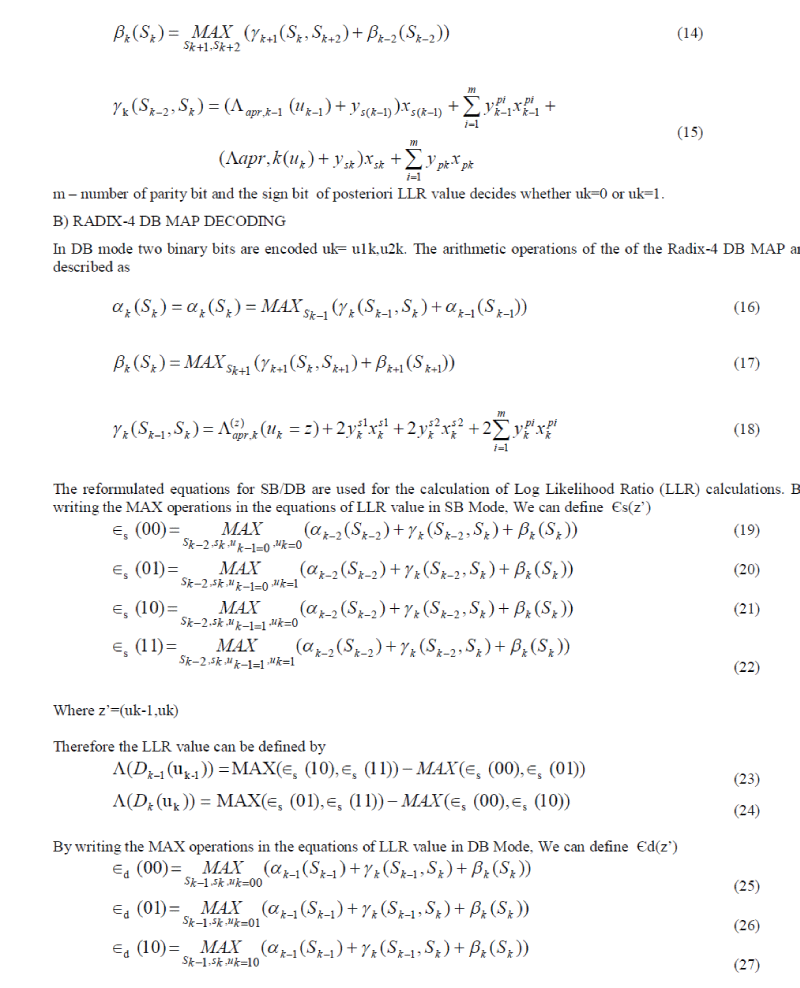 |
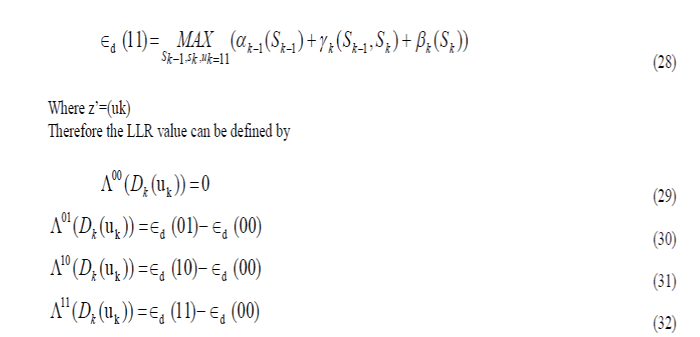 |
| By comparing the LLR values of both SB & DB the MAX operations of ÃÂÃâs(z’) & ÃÂÃâd(z’) are same. Therefore the hardware can be also shared. So, the implementation of this LLR unit in the VLSI tool, the area of utilization is also reduced up to 8 % as existing. |
RESULTS AND DISCUSSIONS
|
| A mathematical model is designed with a jacobian logarithm which consists of a max function along with the exponential correction function. The complexity of the jacobian logarithm is also reduced by the Max Log Map algorithm by eliminating the correction term. Multistep Log Map algorithm is used to approximate the correction function. By this model of correction function the BER of the turbo decoder is greatly reduced. This is shown in the figure 3. A Dual Mode (SB/DB) procedure is used to compute the log likelihood ratio in order to increase the speed of the computation. This method will be incorporated into VLSI technology to design a High Speed MAP Decoder (15% to 25 % as in existing) with less area Utilization (8% as in existing) and low Power (74.95mW). |
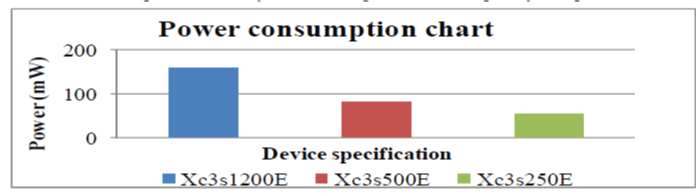
| The proposed decoder can be designed using Verilog HDL, a descriptive hardware language for architectural module design. This designed architectural module is simulated using Modelsim 5.5e simulating tool, synthesized using Xilinx Project Navigator 10.2i synthesis tool and tested on a Spartan3E family device XC3S500E. This proposed scheme utilized 1972 LUTs and 476 FFs at a maximum frequency of 125MHz. The proposed work results shows that the pipelined metric MAP decoding system incorporated with SB/DB mode leads to lower power consumption in terms of slices, Look Up Tables and Flip Flops. |
| The various devices in the Spartan-3 family are tested against their frequency and power and tabulated in Table 1. |
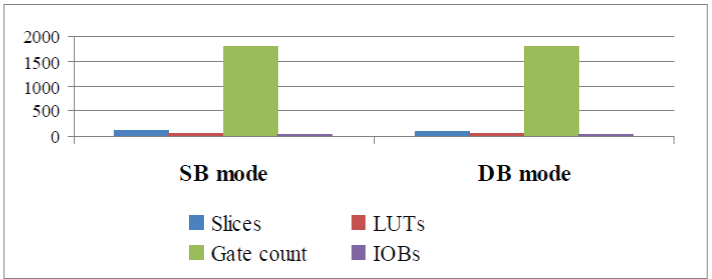
| Table 2 illustrates the investigation parameters, such as number of slices, LUTs, etc. required in SB and in DB mode. The values are graphically plotted and depicted in Fig. 9. |
CONCLUSION
|
| The optimum performance of Log Map Algorithm involves complex operations. By neglecting the correction function in the Max Log Map algorithm gives the capacitive loss and hence the correction term must be added which gives the optimal Log Map algorithm. The shared dual mode MAP decoder achieves low computational costs and low storages. This MAP processor achieves high throughput rates and high area efficiency. |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
Figures at a glance
|
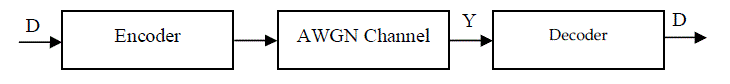 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 7 |
Figure 8 |
Figure 9 |
|
References
|
- C. Shannon, “A Mathematical Theory of Information”, Bell System Technical J., vol. 27, July 1948, pp. 379-423.
- C. Berrou, A. Glavieux, and P. Thitimajshima, “Near Shannon Limit Error-Correcting Coding and Decoding: Turbo-Codes(1)”, Proc. ICC’93,Geneva, Switzerland, May 1993, pp. 1064-1070.
- C. Schurgers, F. Catthoor, and M. Engels, “Memory optimization of MAP turbo decoder algorithms,” IEEE Trans. Very Large Scale Integr.(VLSI) Syst., vol. 9, no. 2, pp. 305–312, Apr. 2001.
- M. M. Mansour and N. R. Shanbhag, “VLSI architectures for SISO-APP decoders,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 11,no. 4, pp. 627–650, Aug. 2003.
- S.-J. Lee, N. R. Shanbhag, and A. C. Singer, “Area-efficient highthroughput MAP decoder architectures,” IEEE Trans. Very Large Scale Integr.(VLSI) Syst., vol. 13, no. 8, pp. 921–933, Aug. 2005.
- L.Bahl,J.Cocke,F.Jelinek and J.Raviv,”Optimal decoding of linear codes for minimizing symbol error rate.” IEEE Trans.Information Theory,Vol.20, PP.284-287, Mar 1974.
- W.J.Gross and P.G.Gulak, “Simplified MAP algorithm suitable for implementation of turbo decoders” Electronics Letters,IET Journal, Vol 34,pp 1577-1578, Aug 1998.
- S.Talakoub,L.Sabeti,B.Shahrrava and M.Ahamadi,”A Linear log Map algorithm for turbo decoding and turbo equalization” IEEE Internationalconference on Wireless And Mobile Computing, Networking and Communications, Vol 1, pp 182-186 Aug 2005.
- Hao Wang, Hongwen Yang and Dacheng Yang “ Improved Log Map decoding algorithm for turbo like codes”, IEEE Communication letters,Vol 10, pp 186-188, Mar 2006.
- P.Robertson,E.Vilebrun and P.Hoecher,”A Comparison of Optimal and sub optimal MAP decoding algorithms operating in log domain”, IEEEInternational conference on Communications”, Vol 2, pp 1009-1013, Jun 1995.
- Y. Sun, Y. Zhu, M. Goel, and J. R. Cavallaro, “Configurable and scalable high throughput turbo decoder architecture for multiple 4G wirelessstandards,” in Proc. IEEE Int. Conf. Appl.-Specific Syst., Arch. Processors (ASAP), 2008, pp. 209–214.
- C.-Y. Chen, C.-H. Lin, and A.-Y. Wu, “High-throughput dual-mode single/double binary MAP processor design for wireless WAN,” in Proc.IEEE Workshop Signal Process. Syst. (SiPS), 2008, pp. 83–87.
- J. Kaza and C. Chakrabarti, “Design and implementation of low-energy turbo decoders,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst.,Vol. 12, no. 9, pp. 968–977, Sep. 2004.
- C.-M. Wu, M.-D. Shieh, C.-H. Wu, Y.-T. Hwang, and J.-H. Chen, “VLSI architectural design tradeoffs for sliding-window Log-MAP decoders,”IEEE Trans. Very Large Scale Integr. (VLSI) Syst., Vol. 13, no. 4, pp. 439–447, Apr. 2005.
- Li F.-M, C.-H. Lin, and A.-Y. Wu, “Unified convolutional/turbo decoder design using tile-based timing analysis of VA/MAP kernel,” IEEETrans. Very Large Scale Integr. (VLSI) Syst., Vol. 16, no. 10, pp. 1358–1371, Oct. 2008.
- T.-H. T. C.-H. Lin and A.-Y. Wu, “A memory-reduced Log-MAP kernel for turbo decoder,” in Proc. IEEE Int. Symp. Circuits Syst. (ISCAS),2005, pp. 1032–1035.
- XiLinx IP Center, San Jose, CA, “Xilinx LogiCORE, IEEE 802.16e CTC Decoder Core,” 2006.
- C.-H. Lin, C.-Y. Chen, A.-Y. Wu, and T.-H. Tsai, “Low-power memory-reduced traceback MAP decoding for double-binary Convolutionalturbo decoder,” IEEE Trans. Circuits Syst. I, Reg. Papers, Vol. 56, No. 5, pp. 1005–1016, May 2009.
- C.-H. Tang, C.-C. Wong, C.-L. Chen, C.-C. Lin, and H.-C. Chang, “A 952MS/s max-log MAP decoder chip using radix-4 4 ACS architecture,”in Proc. IEEE Asian Solid-State Circuits Conf. (A-SSCC), 2006, pp. 79–82.
|