Power Factor Compensation on Distorted
Low Voltage Power Systems

V.Bhanu; Shaik Rafi Kiran

Power Factor Compensation on Distorted Low Voltage Power Systems

V.Bhanu¹, Shaik Rafi Kiran²

PG scholar [EPE], Department of EEE, SITAMS, Chittoor, Andhra Pradesh, India
Professor and HOD, Department of EEE, SITAMS, Chittoor, Andhra Pradesh, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Harmonic resonance has become a major hurdle for performing power factor compensation in commercial power systems, due to the proliferation of harmonic producing-loads. This paper presents an intelligent controller for power factor compensation that can perform power factor correction under varying demand conditions without exciting harmonic resonance. Practical and robust control algorithms are proposed using micro-controller. The controller relies on common low cost sensing devices and hence can be constructed as a retrofitting device to replace existing power factor correction controllers.

Keywords

Capacitor switching, power electronic inverters, harmonic resonance, power factor compensator, transformers, Power Width Modulator(PWM).

I. INTRODUCTION

Energy efficiency is an important factor to commercial areas. The application of power factor (PF) compensation as a necessary step to improve the efficiency of these low voltage electrical installations[1]–[2]. This is usually attained by installing capacitors at the entrance point of the facility downstream to the supply transformer. As the demand for VAR compensation of the building load fluctuates, such capacitor units are switched in and out of circuits. Capacitors can improve the performance of distribution circuits, by providing the reactive current locally, less power needs to be provided by the distribution network resulting in lower losses, improved line voltage, and, lower billing charges. However, these PF correction capacitor banks are subjected to frequent failures or trips. One main reason is the proliferation of harmonic-producing loads. Though these devices do not generate harmonics, they provide a network path for local or parallel resonance conditions. In case of resonance, this current may be very high and may damage the capacitors. Therefore, the consideration of PF compensation capacitor installation at the design stage [1]–[2] should also include harmonic resonance analysis . Possible solution to avoid harmonics include the following:

1) adding a filter capacitor;

2) adding a reactor to an existing bank;

3) ungrounding grounded-wye capacitors;

4) changing capacitor bank locations and sizes; and

5) In order to avoid resonance, controlling the capacitor switching scheme.

This paper covers the fifth approach and consists of improving a robust and practical control algorithm for the capacitor bank switching scheme which is capable of attaining both power factor correction and avoid resonance. Previously proposed optimization algorithms for the same purpose are time-consuming and not guaranteed that they converge to the optimal solution under time-varying load and system impedance conditions. More recent works have focused on installation of active and passive harmonic filters. This approach may be complex and costly. Other solution is to add reactors in series with existing capacitor banks. However, the system parameters vary dynamically with the power system configurations and loads. Therefore, the harmonic resonance can be achieved even if a combination of capacitors are connected in series with reactors. Reference [4] proposes replacing reactors with power electronics inverters. Under varying demand conditions the resonance varies for different operating conditions, it is not safe and intelligent to decide the suitable number of switched capacitors units assuming constant system impedance. In order to solve the same, the proposed controller uses pre- and post disturbance steady-state waveforms to estimate the harmonic system impedance of the voltages and currents at the interface point. It is highlighted that the proposed controller relies on common low cost sensing devices. As a result, with little effort the controller can be constructed to replace existing power factor correction controllers.

II. RELATED WORK

Though correction of power factor is old practice,we have considered the work done in the last 25 years in our survey, starting from 1983. Jones and Blackwell proposed a technique for maintaining a synchronous motor at unity power factor from no-load to full load assuring peak efficiency. Sharkawi proposed an adaptive power factor controller for three-phase induction generators. Nalbant proposed the calculations and measurements of power factor correction and distortion reduction using the peak current programmed boost topology. Fuld proposed a combined buck and boost power factor controller for three phase input. Mandal proposed a laboratory model of a micro computer based power factor controller for compensating reactive power. Ayres and Barbi proposed conventional integrated circuits for PWM and power factor controllers. Machmoum proposed a 3-phase switching converter, acted as a PWM rectifier and as an active power filter. Barsoum proposed the programming of PIC microcontroller for power factor correction.

III. COMMON REACTIVE POWER COMPENSATION SCHEME

In commercial facilities, the traditional approach for power factor compensation consists of capacitor banks in parallel with the load offsetting the inductive loading of the equipments at the entrance point of the facility. Fig. 1 shows a common power factor compensation arrangement used in commercial power systems.

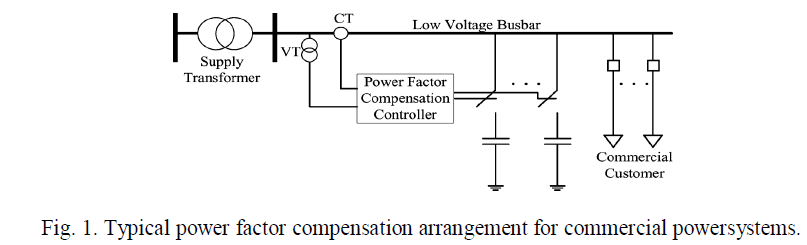This scheme consists of one or more breaker switched capacitor units along with an intelligent control unit, current and voltage transformers, which areconnected at the low side of the supply transformer. These banks include 3 to 9 capacitor units connected in different configurations. In practice, commercial installations employ switched capacitor banks, instead of fixed banks, in which the capacitors are switched on and off automatically to compensate for changing load conditions. Fig. 2 shows a typical kilovar demand over a 24 h period where the curve is determined byrecording kilovar meter and pf measurements.

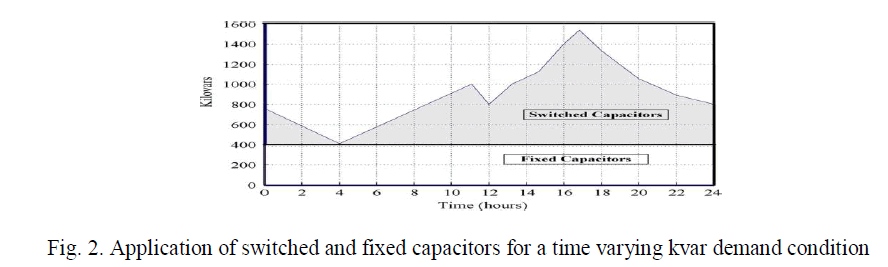The fixed banks satisfy the base load requirements, and the switched banks compensate for the inductive kilovar peak during the heavier load periods. In order to calculate the capacitive kilovars one must subtract the inductive kvar of the corrected pf from the existing pf. The difference is the amount of capacitive kvar to be added. The following formula is a convenient way of doing this:

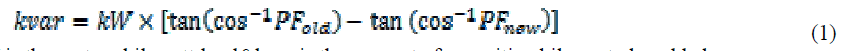Where, kW is the system kilowatt load&kvar is the amount of capacitive kilovar to be added. The capacitor switching control scheme illustrated in Fig.1 is based on automatic controller. The control senses voltage and current, and uses either these parameters directly or a derived parameter like power factor to compare against a threshold. Fig. 3 shows a flowchart.

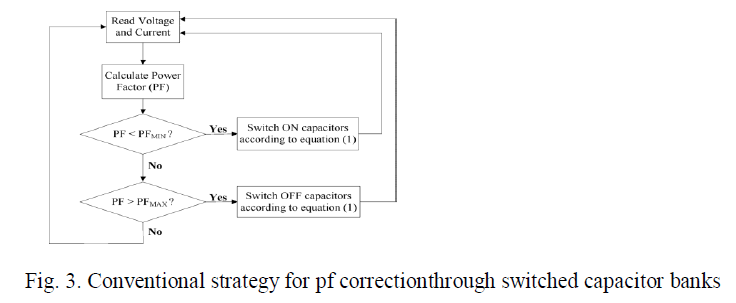Based on the above considerations, automatic capacitor controllers have been developed&marketed for commercial power system designersand operators. While such controllers work well for traditional passive loads such as motors, more and more facility operators have reported frequent capacitor failures or trips. As a result, reactive power compensation cannot be achieved. This problem is caused by the parallel resonance between the capacitor and the upstream impedance. This resonance is excited by the harmonic currents produced by modern facility loads such as office electronics and variable frequency drives. Industrystrongly needs capacitor controllers that can perform power factor correction and avoid harmonic resonance. In addition, the controller shall not require additional sensors or inputs and can retrofit current controllers with zero alteration to the existing facility.

IV. HARMONIC RESONANCE PROBLEM

There is always the risk of resonance with capacitor banks application. This is due to the interaction of the bank’s capacitance with the inductive reactance. Harmonic currents at or near the resonant frequency can create high harmonic voltages across the high parallel impedance and the capacitor may not be able to withstand the resonance voltage. In order to facilitate the description of the resonance problem, Fig. 4 is used to represent a harmonic-producing commercial facility with a shunt PF correction capacitor connected at the PCC with the distribution system. In this figure, the impedance and current source represent the linear andnonlinear loads of the facilities, respectively.

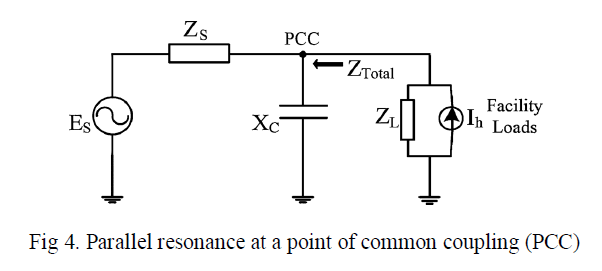Assume that the supply system can be represented by a Thevenin impedance of

where h is the harmonic order. The total impedance Ztotal seen by the harmonic current source can be determined as

The inductive reactance Xs of the supply system impedance increases and the capacitive reactance Xo decreases as the frequency increases, or as the harmonic order increases. There will be a crossover point where the inductive and capacitive reactances are equal (h2Xg =xo ) , at a given harmonic frequency. Consequently, the total impedance (Ztotal ) approaches infinity and a very high voltage harmonic may result if the commercial facility harmonic current has a frequency close to

Where MVAs is the system short-circuit level and Mvarc is capacitor size. The above frequency is called the resonance frequency. In this case, the resonant components Xc and Xs are in parallel. The resulting resonance is called parallel resonance. The parallel resonance phenomenon can be visualized from a frequency scan plot,as shown in Fig. 5.

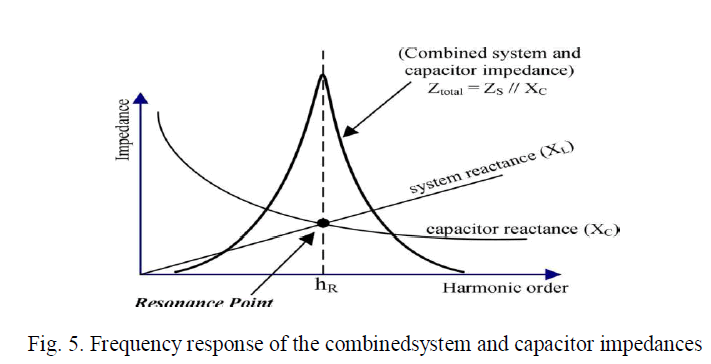This figure illustrates how both system and capacitor reactances change with the frequency. At the resonance frequency both reactances are equal and total impedance seen from the capacitor location Ztotal will tend to a very large value.Consider a system fault level of 250 MVA and a capacitor bank rating of 10.8 Mvar. Substituting these numbers on (3) yields:

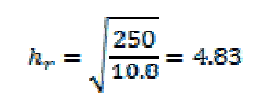The parallel resonance order of 4.83 is too close to the 5th harmonic order and if any magnitude of 5th harmonic current flows from the harmonic-producing loads into the power system at the capacitor bus, the capacitor may not be able to withstand the resonance voltage, leading to fuse blowing or capacitor damage. A practical (rule of thumb) way to find out whether parallel resonance should be a concern is to use (4), which shows how further away the resonance frequency hR should be from any dominant harmonic frequency hC

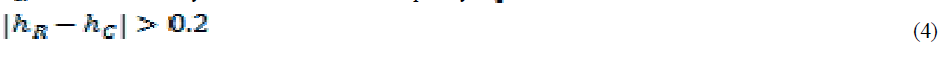However, the condition given by (4) is not sufficient because resonance frequency shift can occur due to capacitance deviation. Therefore, the final condition to decide if a certain combination of capacitors should be switched is to verify if the stress levels on the capacitors bank meet the limits defined in Table I.

When large levels of voltage and current harmonics are present, the ratings are quite often exceeded, resulting in failures. Therefore, the consideration of power capacitor installation should include harmonic resonance analysis at the design stage. The installation of filters can bring unacceptable additional operational and capital costs to the PF correction scheme and, furthermore, a detailed harmonic study must be conducted to ensure that the application of the filters will not cause other side effects on both the facility and the distribution power system, such as parallel resonance at harmonic frequencies other than the one targeted by the filter. We think that focusing on a more intelligent algorithm to control the capacitor switching scheme to achieve both power factor correction and avoid resonanceunder varying demand conditions. Employ an adaptive control to monitor the harmonic distortion and switch the capacitors to avoid resonance might be appropriate for commercial loads where there are numerous switched capacitors coming on and off line randomly. Basically, the idea is to develop a controller that relies on common low cost sensing devices. As a result, the controller can be constructed as a retrofitting device to replace existing power factor correction controllers with little effort.

V. PROPOSED CONTROL ALGORITHM

Based on the previous discussion, the problem to be solved is to determine the number of capacitor units to be switched that can yield the highest power factor for the facility without causing excessive harmonic stress on the capacitors. Since there are limited numbers of capacitor combinations, the simplest algorithm is to scan through these combinations and pick the best. Such an approach complicates the problem, it is not guaranteed to converge and it might be time-consuming. More importantly, they cannot be easily implemented into a micro-controller. In this paper, a practical, efficient, and robust algorithm is proposed. Easy implementation is one of the main consideration. It is important to note that the switching control algorithm is only one of the components of the controller. The algorithm needs the system impedance information as input. There is also a need to detect if a capacitor is being overstressed due to changing harmonic conditions. Therefore, the proposed controller actually has at least the following three major functions:

A. Measurement of the System Impedance

In the previous section, it was discussed that in order to detect a resonance condition, it is necessary to determine the system impedance. One important issue is that the system impedance is not constant, but varies due to loading and topological changes on the system. Therefore, the following issue must be solved, how the harmonic resonance condition can be determined for a time varying load demand and topology? A number of impedance measurement methods have been developed, which can be classified into two types: the transients-based methods and the steadystate- based methods. The transients-based methods inject transient disturbances into the system. The frequencydependent network impedances are extracted from voltage and current transients. The main problems associated with these methods are the need for a high-speed data acquisition system and for the source of disturbances. The steadystate- based methods use pre- and postdisturbance steady-state waveforms. Typical disturbances are harmonic current injections produced by an external source or switching of a network component. Since there are no transients involved, the methods can only determine network impedances at harmonic frequencies. Since there is no need for a high-speed data acquisition system, the steady-state method can be implemented with many common, low-cost power quality monitors and it relies on the common voltage and current transformer sensors illustrated on Fig. 1. The simplest form of the steady-state measurement method involves the switching of a network component at the location where the network impedance is to be measured. The basic idea of this method can be summarized as follows:

1) Record the steady-state waveforms of the capacitor voltages and currents. If the capacitor is not connected, its currents are treated as zero.

2) Changes are then made to the status of the capacitor. For example, a capacitor unit can be switched on or off to meet the power factor requirement.

3) The postdisturbance steady-state voltage and current waveforms are recorded.

4) Discrete Fourier transform (DFT) is applied to the pre- and postdisturbance waveforms. For each harmonic, the following system equations can be developed:

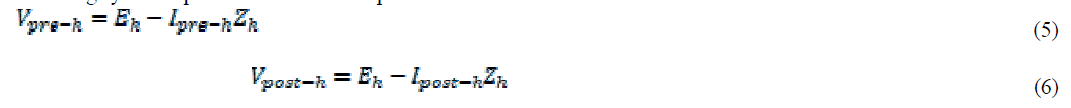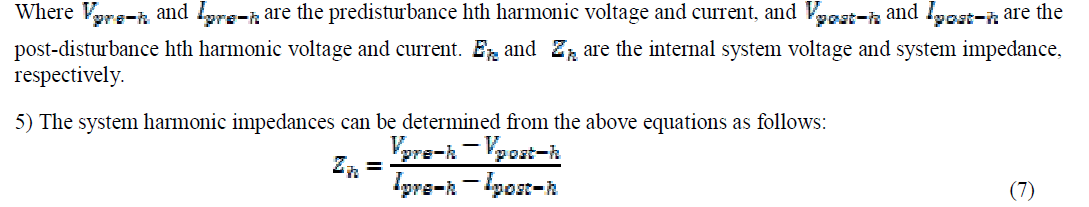B. Detection of Resonance Condition

As mentioned before, from the system impedance and the existing capacitor impedance, the resonance frequency can be calculated through (3). For a certain system impedance, the number of capacitor units that lead to a harmonic resonance frequency equal or close to the dominant harmonic frequencies. Fig. 6 illustrates, for a particular system impedance, how the harmonic resonance frequency changes as more and more capacitor units are switched on. For the figure, the system is represented by a transformer of 1600 kVA with reactance of 6.0% and each capacitor unit has a capacity of 50 kvar.

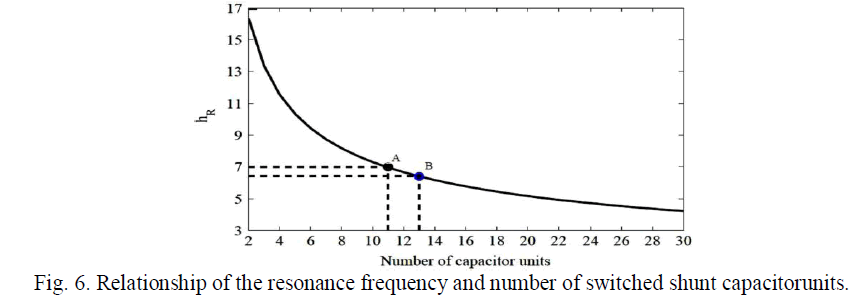From figure, it is clear that the resonance frequency can be shifted from a harmonic frequency by changing the number of switched capacitor units. A practical way to verify if hR is too close to any harmonic frequency hC is to apply (4). From Fig. 6, if 11 capacitors are switched ON, the resonance frequency hR is too close to the 7th harmonic order(point A), therefore, the bank should be increased or decreased. If two more capacitor are switched (13 in total), hR is around 6.4 (point B), which is further away from 5th and 7th harmonic orders. However, it is also necessary to evaluate for the current combination of capacitor units if its loading conditions meet the limits specified by Table I. One can also observe from Fig. 6 that more than one combination of capacitor units can be considered to avoid resonance. In this paper, each combination refers to a particular number of capacitors to be switched on to the circuit.

C. Determination of Capacitor Units

The final step is to determine the number of capacitor units that can be switched without violating power factor and resonance constraints. From the previous subsection, it is possible to estimate, from the current system impedance, the combinations of capacitor units that can be switched so that the resonance frequency ( hR) is further away from the harmonic frequencies. This can be done through the following steps:

1) The system impedance MVA3 2) Substituting (3) in (4) yields (8), from which it is possible to determine the combinations of capacitors Mvarc that can be switched. Normally, the dominant harmonic frequencies hc are the odd harmonic orders from 3 to 29calculated from the last capacitor switching is used as input.

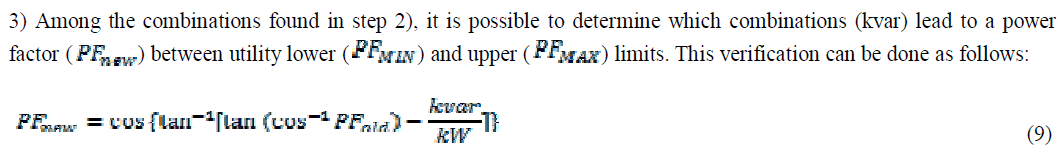4) From the combinations found in step 3), select the combination that lead to minimum switching relative to the current capacitor bank configuration.

5) Calculate the anticipated loading for this combination using the indices present in Table I.

6) If loading indices meet the standard limits, switch the combination, otherwise go back to step 4) to select a suboptimal solution.

VI.RESULTS AND ANDVANTAGES OF PROPOSED ALGORITHM

• It does not require additional measurements relying on common voltage and current transformer sensors.

• The controller does not require the installation of reactors and filters.

• The controller not only checks if the harmonic resonance frequency is further away from any harmonic frequency, but the capacitor stress levels are also verified to ensure the selection of the most appropriate combination of capacitor units.

• The controller takes into account the time-varying system conditions to determine both the power factor and the resonance condition.

• The proposed controller also preserves the objective of conventional controllers, which is to achieve the highest facility power factor.

VII. CONCLUSION

This paper presents a new control strategy for power factor compensation on distorted low voltage power systems. The proposed strategy can perform power factor correction without exciting harmonic resonance under varying demand conditions. Practical and robust control algorithms are proposed for the purpose of easy implementation in a microcontroller. In addition, the controller relies on common low cost sensing devices and does not require additional hardware circuits. As a result, the proposed controller can be constructed as a retrofitting device to replace existing power factor correction controllers with little effort and low cost.

References

T. M. Blooming and D. J. Carnovale, “Capacitor application issues,” IEEE Trans. Ind. Appl., vol. 44, no. 4, pp. 1013–1026, Jul. 2008.1570 IEEE TRANSACTIONS ON SMART GRID, VOL. 3, NO. 3, SEPTEMBER 2012
A. Novitskiy and H. Schau, “Energy saving effect due to the voltage reduction in industrial electrical networks,” in Proc. Elec. Power Quality Supply Rel. Conf. (PQ), Jun. 2010, pp. 67–72.
L. Herman and I. Papic, “Hybrid active filter for power factor correction and harmonics elimination in industrial networks,” in Proc. IEEE Electr. Power Energy Conf. (EPEC), Oct. 2011, pp. 302–308.
P. Jintakosonwit, S. Srianthumrong, and P. Jintakosonwit, “Implementation and performance of an anti-resonance hybrid delta-connected capacitor bank for power factor correction,” IEEE Trans. Power Del., vol. 22, no. 6, pp. 2543–2551, Nov. 2007.