Quadtree Segmented Double Predictor DPCM
Image Compression

Jia-Chyi Wu

Quadtree Segmented Double Predictor DPCM Image Compression

Jia-Chyi Wu
Assistant Professor, Dept. of Communications, Navigation and Control Engr., National Taiwan Ocean University, Keelung, Taiwan

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

This study is to improve image data compression performance based on variable block-size quadtree image segmentation applied to double predictor differential pulse code modulation (DP–DPCM) image compressive algorithm. The quadtree segmentation method is applied to better allocate image characteristics. A variable block-size double predictor DPCM (VBDP–DPCM) image coding system works on an image been preprocessed into segments of variable size, square blocks, and each block is separately encoded by a DP–DPCM algorithm. Quadtree segmentation method is utilized to divide a given real-world image into variable size image blocks. The detail regions comprise more image features of a given image is segmented into blocks with smaller block size, and the background regions of the image will be assigned larger block size to the image blocks. After quadtree segmentation process, the average dissimilar values between the nearby pixels within an image block are abridged. Therefore, we can decrease the distribution range of the prediction error anddiminish the quantization levels as well as the coding bit rate. We then adopt the double predictor DPCM technique to moderate the effect from the fed-back quantization error and not to augment the system complexity. The compression performance of this proposed method is about 5dB (or greater) coding gain in Signal-to-Noise Ratio (SNR) than that of a conventional DPCM system.

Keywords

variable block-size;quadtree segmentation; differential pulse code modulation (DPCM); double predictor estimation

INTRODUCTION

The proposedquadtree segmented variable block-size double predictor differential pulse code modulation (VBDP– DPCM) image coding system operates on an image that has been preprocessed into segments of variable size, square blocks. A double predictor DPCM (DP–DPCM) system is then applied to encode each image sub-block separately. When transmitted over a noiseless channel, the distortion between the original signal and reconstructed signal is primarily due to quantization error provided that an optimal predictor is employed. Reconstructed signal degradation because of quantization error becomes severe at low bit rates due to the fact that large quantization errors are directly fed back into the predictor and to be used in subsequent estimation of future input signal [1]. The proposed VBDP– DPCM algorithm has been establishedto moderate the feedback loop quantization error effects in the vicinity at the expense of predictor optimality from a minimum mean-squared-error (MMSE) point of view. This VBDP–DPCM scheme divides a given image into variable size image sub-blocks and attempts to balance between sub-optimal predictor designs. The proposed scheme mayexpressively reduce feedback effects due to quantization errors locallywith the objective of maximizing reconstructed image quality for each test image entirely.

When processing a given image frame, we initially apply the quadtree segmentation algorithm [2]–[4], [11]–[14] to divide a given test image into image sub-blocks having widely differing perceptual importance. The detail regions of a given image with more features activity will be segmented into blocks with smaller block size, and the background inactive regions of the image should be assigned larger block size for the areas. The block-sizes can vary from 128x128 to 8x8 in this study. The variable block-size image segmentation processis to better meet the non-stationary mathematical description of real-world images. Having acomprehensive characterization of the underlying stochastic nature of a source signal generally results in a more efficient source encoder for that signal. After the quadtree image segmentation, the predicted differential values between the nearby pixels of an image block are reduced. Therefore, we can decrease the distribution range of prediction error and reduce the bit rate as well as quantization levels. We then applied the DP–DPCM [6]–[8] scheme to each image sub-block. As in the case of conventional DPCM image coding system the emphasis of system design is focused on the prediction process which should reduce MMSE estimates of the input signals. Similarly, quantizer design is based on a match to the probability density function of a differential signal. The quadtree image segmentation method applied is to divide a given image according to the activity details within the image into variable size image sub-blocks. Each image sub-block will be more stationary than the original image frame and the predicted differential values between the nearby pixels of an image sub-block are condensed. The quantizer design employed in the encoder is locally optimal in the MMSE sense. Experimental results have been obtained by processing two test images named,“LENA” and “WALT”. Objective measurement of system performance shows that the SNR obtained using the VBDP–DPCM scheme is about 5 dB or greater compared to that of conventional DPCM employing a predictor of the same order for low bit rate (R? 3) image compression.

In this paper, Section II describes the basic concepts regarding a conventional 2-D DPCM image encoder scheme as well as a double predictor DPCM encoder algorithm proposed earlier. Section III focuses on the proposed quadtree variable block-size image segmentation applied to a double predictor DPCM image compression applied in this study. The overall VBDP–DPCM image encoding system configuration and performance results are shown in Section IV. Finally, a summary and conclusions are presented in Section V.

RELATED WORK

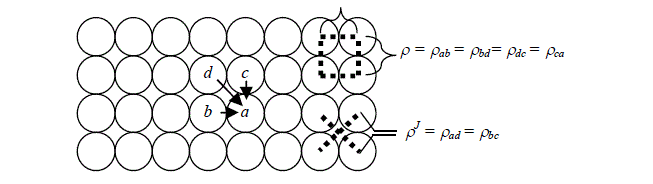
In a conventional 2-D DPCM image encoder having a feedback loop around the quantizer, the prediction sequence values ij xˆ depend on the previously quantized error values ij x ~ rather than on past unquantized input data values xij. This ensures that the transmitter and receiver components of the DPCM system can track and reconstruct the input signal waveform in a stable fashion. For a given NxN image with pixel intensity values xij,i, j = 0, 1, …,N–1, a typical 2-D causal image predictor having third-order support used to determine the estimation sequence is described by

which can be compactly express as

where bx, cx, and dx are the predictor coefficients of the DPCM predictor and b x ~ , c x ~ , and d x ~ are the data values input to the predictor filter corresponding to locations b, c, and d in the image field, as shown in Figure 1.

Let P denote the one-lag covariance

where J = 2 for an image model with separable auto-correlation function and J = 2 for an isotropic image model [5]. The optimal third-order predictor is defined by the prediction coefficients:

Performance for the conventional DPCM systemis shown that the quantization in the encoder loop is not adequately fine if the encoding rate is 3 bits/pixel or less, the quantization error is not small enough so as to be ignored in the design of the optimal linear predictor.In order to balance between sub-optimal predictor designs and significantly reduce feedback effects due to quantization errors with the objective of maximizing reconstructed image quality, a double predictor DPCM algorithm has been proposed [6].

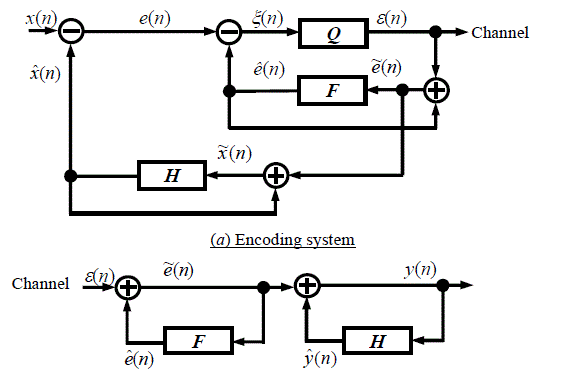
Figure 2 illustrates the block diagram of a DP–DPCM algorithm. The corresponding DPCM decoder consists of two cascaded filtering stages. The DP–DPCM scheme has an overall structure similar to that of a double differentiatorintegrator system[9]. Filter coefficient values are chosen under constraints that guarantee system stability. There are two predictor filters, H and F in this scheme, where Q is a PDF-optimal quantizer of either a uniform or non-uniform structure. The output of the first subtractor, e(n), is input to a second subtractor whose other input is a local estimate of the differential signal itself. The output signal ?(n) is the difference sequence e(n)–ê(n). The quantizer output sequence ?(n) is fed back into the adder along with the estimationê(n) of e(n) producing e~(n)which is the input to the filter F and to the primary prediction loop. Conceptually, e~(n)should be statistically closer to the prediction error e(n) rather than the quantizer output signal ?(n).

The predictor coefficients can be written as

We have assumed that the average value E[e(n)]=0, the one-lag covariance of e(n), ? e is then defined as

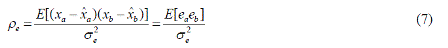where a x ~ and b x ~ are defined as in eq. (2), 2 σe is the variance of the error sequence e(n)and E[eaeb] is the error correlation. For 2 σe ; is of the form as following [10]

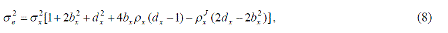we can obtain the covariance ? e to be of the following equation

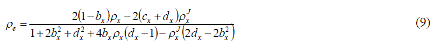We now are able to calculate the optimal filter coefficients of predictor F by substituting ρ e andρ e J into eq. (5) and eq. (6). The variance of the difference sequence appearing at the output of the second subtractor is given by

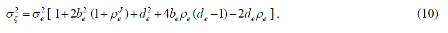where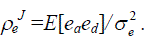

The variance of ξ(n) = e(n)–ê(n), denoted as 2 σ ξ , and the square root, σξ (standard deviation of ξ(n)) is the parameter adjusting the dynamic range of the locally optimal quantizerQ.

PROPOSED ALGORITHM

To improve image data compression performance further, we have proposed a combined system based on variable block-size quadtree image segmentation applied to double predictor differential pulse code modulation (DP–DPCM) image compressive algorithm.

Ina variable block-size image compression system, we segment the input image into variable size blocks, for which a “detail” region comprisingmore image features activity is partitioned into a smaller block size, each sub-image blockcan be moresensibly described the appearances in the region, and a “background” region with less image variationis assigned a larger block-size. We have espoused a top-down quadtree approach [2] to obtain the tractability of a variable block-size segmentation procedure while eluding the excessive overhead needed to characterize more sophisticated image segmentation techniques. To segment a 256x256 image by using the quadtreeprocedure, we begin with dividing a given 256x256 input image into four 128x128 equal size blocks. Each 128x128 image block is set to be a root(initial node), from which the algorithm passes through the tree from level to level. At each node, a test is executed to determine whether the image blockrepresented by that node is a “background” region or a “detail” region. If the test agrees that the block is a “background” region, then the node becomes a leaf. If not, the segmentation proceeds to the next level and the four branches of the node are each examined consecutively. The final quadtree structure is represented by one bit of side information for each node, which indicates whether that node is a nonleaf or a leaf node. By adapting the predictor and quantizer structures for each variable size image block the statistical nonstationary inherent in real-world images is competentlyrevealed. Encoding efficiencies are realized by: (i) achieving better edge renovation in busy areas of an image; (ii) considerable rate reductions in areas of near-constant gray level which is characteristic of the larger block size regions within an image.

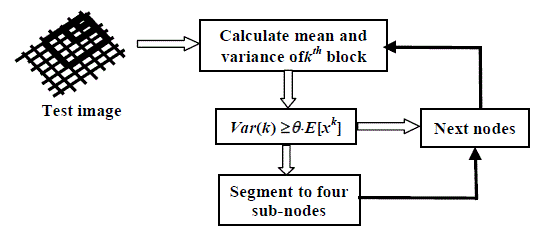
The segmentation test used in this study is implemented as follows: For kth image block xk mn, we first estimate the mean value, E[xk], and the variance, Var(k).Then, we compare the value ofVar(k) with?θE[xk], where ??is a preset threshold. The quadtree segmentation threshold value θ was first picked randomly large and should be reduced to deal with the anticipated distortion until a tolerable reconstructed image quality achieved. If Var(k)≥ θE[xk] for the examined image block, then the block is marks as a “detail” region and the segmentation course proceeds to the next level. The test procedure of the quadtree algorithm is illustrated in Figure3.

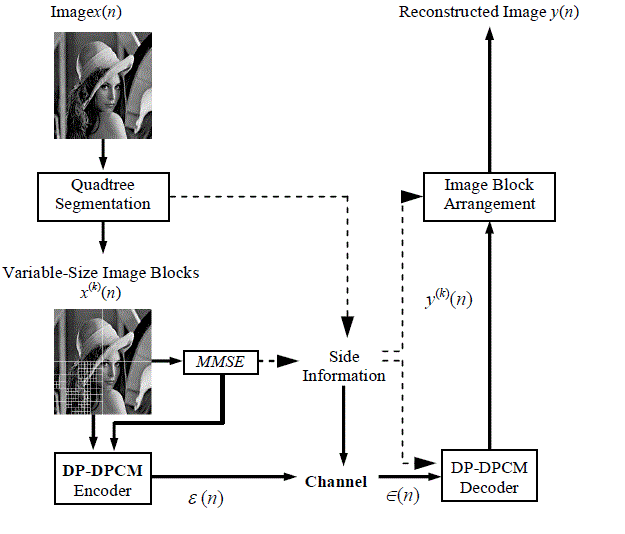
Figure 4 presents the proposed variable block-size double predictor DPCM image coding system,which improves the performance of DPCM by adapting the predictor and quantizer structures for each variable size image block. For the VBDP–DPCMimage coding, an NxN image with pixel intensity values xij,i, j = 0, 1, …,N–1, is segmented into blocks of size MkxMk, where the block size can vary from 128x128 to 8x8. The pixel values of thekthsub-image block is denoted by xk mn, m, n = 0, 1, …,Mk –1, and is expected to possess statistical stationary over the spatial domain.

For each segmented image block, the first-order and second-order statistics are estimated over an entire sub-block of image data. Hence, the complete image frame retains globally statistical non-stationary over the spatial domain. The local mean is determined and subtracted from the MkxMk image block to obtain a zero-mean image block. To be simplified, quantizers with uniformly spaced output levels were designed on the basis of a Laplacian probability density function (PDF) describing the differential input sequences for each image block. A third-order predictor structure is used both for the prediction of xˆ(n) of the image signal based on ~x(n) and for the prediction of the difference signal ê(n) based on e~(n) . Follow the procedures delivered in [8], the design process is modified and outlined in the following steps.

Step 1: For a given image, we apply the quadtree segmentation algorithm to divide the image into variable size image blocks having widely differing perceptual importance. Estimations of the local mean value, variance, and covariance coefficient ρ x for each image block are provided.

Step 2: The local mean is deducted from the pixels’ value in each image block to obtain a zero-mean image block.

Step3: Determinethe optimal predictor coefficients,bx,opt,cx,opt,dx,optfrom eq. (3) and eq. (4). For the predictor coefficients values (bx,opt,cx,opt,dx,opt), compute the corresponding variance σ2e of the error sequence e(n)and E[eaeb], the error correlation for the second-stage filter F.

Step 4: With the values of variance 2 e s and E[eaeb], we can calculate ρ e J =E[eaed]/ 2 e σ and ρ e. We then substitute ρ e J and ρe into eq. (5) and eq. (6) to solve the optimalprediction coefficients (be, ce, de) for the second-stage filter F.

Step 5: The coefficients (be, ce, de) are substituted into eq. (10) to calculate the variance 2 σξand then the standard deviation, σξof ξ(n). σξ is the parameter to adjust the dynamic range of the locally optimal quantizerQ.

Step 6: For each zero-mean image block, we can determine the predictor coefficients based on the previous steps. The difference sequences after the second-stage predictor can be quantized with the step-size determined in step 5 and then output to channel.

SIMULATION RESULTS

The source coding performance of the proposed variable block-sizeDP–DPCM system presented in this study is generally about 5 dB or greater than that of a conventionally design DPCM system when operating at low bit rates (bit rate R≤3 bits/pixel). Noteworthy improvement in performance can be denoted for values of coding rateR greater than 3. Simulation results obtained in this study are summarized in Tables I and II. The output signal-to-noise ratio (SNR) is defined as SNR=10log( 2 x σ / 2 e σ )in dB, where 2 x σ is the input image variance and 2 e σ is the reconstructed error variance. Shown in TablesI and II are the image coding results for the VBDP–DPCM system for 256x256 “LENA” and “WALT” images, respectively. The source coding performance of the VBDP-DPCM system has higher SNR compared to a conventional stationary-based DPCM system in general. The reconstructed images using the scheme in Figure 4 are mostly of higher quality both subjectively and objectively. Values of SNR equal to 12.68 dB, 17.57 dB, and 22.71 dB are obtained for the 256x256 “LENA” image at the rates of 1, 2 and 3 bits/pixel, respectively, for threshold θ = 5. Values of SNR equal to 16.23 dB, 20.62 dB, and 24.81 dB areachieved for the “WALT” image at the rates of 1, 2 and 3 bits/pixel, respectively, for threshold θ = 5. These results are better than those found using a conventional, stationary DPCM encoder/decoder system.

Figure 5 compares the subjective quality of reconstructed “LENA” images obtained with the VBDP–DPCM system (θ = 5) to the quality obtained with a stationary, conventionally designed DPCM encoder at transmission bit rates R = 1 bit/pixel. The reconstructed image shown in Figure 5(d) faithfully reproduce gray-level variations in regions of high spatial activity, e.g., the feathers in the “LENA” image are sharper as compared to the blurring present in Figure 5(a), the results for the conventional DPCM encoder. Figure 6 and Figure 7show the visual quality of the reconstructedVBDP-DPCM“LENA” and “WALT”images at different coding rates of 1, 2, and 3 bits/pixel, respectively. The decoded imagesnormally have slightly sharper image details, dueto the AR predictionsadapted to local statistics, as well asthe filtering operation to moderate the venomous effects of quantization errors being fed back into the prediction loop of the DPCM code as shown in Figure 2(a).

CONCLUSION AND FUTURE WORK

The new double predictor DPCM coding system with variable block-size investigated in this study results in improved source coding performance when compared to a conventionally designed DPCM image encoding scheme for bit rate R≤ 3 bits/pixel. Objective SNR results demonstrate that the new VBDP–DPCM encoding scheme yields better reconstructed image quality vis-a-vis conventional, stationary DPCM image encoding system. Performance improvements are the results summarized as:

• Image segmentation results in the statistical non-stationary inherent in real-world images being better exploited;

• The DP–DPCM encoding scheme is applied to each segmented sub-image block. We are able to adapt the predictor and quantizer structures for each variable size image block;

• The balance in design of sub-optimal difference signal predictors and a filtering operation to reduce the deleterious effects of large quantization errors being fed back into the prediction loop for small values of R.

The source coding performance of the variable block-size DP–DPCM algorithm is generally about 5 dB or greater than that of a conventionally designed DPCM coding system when operating a low bit-rates. The improved DPCM system provides better edge reproduction that is perceptually important to the viewer.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3

Figure 4	Figure 5	Figure 6

References

Jain, A. K., “Image Data Compression-a Review,” Proceedings of IEEE, Vol. 69, no. 3, pp. 349-389, March 1981.

Vaisey, J. and Gersho, A., “Image Compression with Variable Block Size Segmentation,” IEEE Transactions on Signal Processing, Vol.40, No.8, pp. 2040-2060, Aug. 1992.

Chen, C. T., “Adaptive Transform Coding via Quadtree-Based Variable Blocksize DCT,” Proceedings of ICASSP, Vol.3, pp. 1854-1857, May 1989.

Wu, J.-C.andDaut, D. G., “Adaptive Nonstationary DPCM Image Coding with Variable Blocksize,”Proceedings of the SPIE Visual Communications and Image Processing (VCIP) 1997, Vol.3024, pp. 447-458, San Jose, CA, February 1997.

Sakrison, D. J., “Image Coding Applications of Vision Models,” Advances in Electronics and Electron Physics, Vol.12, pp. 21-71, 1979.

Daut, D. G., Zhao, D.-M., and Wu, J.-C., “Double Predictor Differential Pulse Code Modulation Algorithm for Image Data Compression,” Optical Engineering, Vol.32, No.7, pp. 1514-1523, July1993.

Chen, H.-B.,“Advanced Double Predictor Differential Pulse Code Modulation Image Transmission System,” Master’s thesis, EE dept., Dayeh University, Chang-Hua, Taiwan, July 1998.

Wu, J.-C.,Chen,H.-B., and Liu, R.-J.,“Variable Block-Size Double Predictor DPCM Image Coding”, Proceedings of SPIE Visual Communications and Image Processing (VCIP) 2000,Vol.4067,pp. 838-847, May 2000.

Nasseri, Z. and Kanefsky, M., “Doubly Adaptive DPCM,” IEEE Transactions on Information Theory, Vol.36, No.2, pp. 414-420, March 1990.

Tekalp, A. M., Kaufman, H., and Woods, J. W., “Fast Recursive Estimation of the Parameters of a Space-Varying Autoregressive Image Model,” IEEE Transactions on Acoustic Speech Signal Processing, Vol.ASSP-33, pp. 469-472, April 1985.

Hunter, G. M. and Stieglitz,K., “Operations on Images Using Quad Trees,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol.PAMI-1, No.2, pp. 145-153, April 1979.

Markas, T. and Reif, J., “Quad Tree Structures for Image Compression Applications,” Information Processing & Management, Vol.28, No.6, pp. 707-721, 1992.

Dhanalakshmi, S. andRavichandran, T., “A New Method for Image Segmentation,” International Journal of Advanced Research in Computer Science and Software Engineering, Vol.2, No.9, pp. 293-299, 2012.

Chen, W.-L.,Hu, Y.-C., Liu, K.-Y.,Lo, C.-C., and Wen, C.-H.,“Variable-Rate Quadtree-segmented Block Truncation Coding forColor Image Compression,” International Journal of Signal Proc., Image Proc. and Pattern Recognition, Vol.7, No.1, pp.65-76, 2014.