We suggest an algorithm that allows (i) each node to detect when the connectivity to a particularly chosen node has been lost, and (ii) one or more nodes (that are connected to the special node after the cut) to notice the incidence of the cut. The algorithm is dispersed and asynchronous: every node wants to converse with only those nodes that are within its message range. The algorithm is based on the iterative calculation of a fictitious “electrical potential” of the nodes. The meeting rate of the underlying iterative scheme is self-governing of the size and arrangement of the network. We demonstrate the effectiveness of the proposed algorithm through simulations and a real hardware implementation. In this paper, employ a sensible restricted random mobility model, we try to fill this gap. Specifically, we suppose that a network of unit area with n nodes is evenly divided into cells with an area of n each of which is further evenly divided into squares with an area of n . All nodes can only move inside the cell which they are at first dispersed in, and at the start of each time slot, every node moves from its current square to a uniformly chosen point in a time after time chosen adjacent square. By proposing a new multi hop relay scheme, we there smooth trade-offs between throughput and delay by scheming nodes’ mobility. We also consider a network of area n and find that system size does not affect the results obtain before.
INTRODUCTION |
| In this article we propose a distributed algorithm to detect cuts, named the Distributed Cut Detection (DCD) algorithm.
The algorithm allows each node to detect DOS events and a subset of nodes to detect CCOS events. The algorithm we
propose is distributed and asynchronous: it involves only local communication between neighboring nodes, and is
robust to temporary communication failure between node pairs. A key component of the DCD algorithm is a distributed
iterative computational step through which the nodes compute their (fictitious) electrical potentials. The convergence
rate of the computation is independent of the size and structure of the network. The DOS detection part of the algorithm
is applicable to arbitrary networks; a node only needs to communicate a scalar variable to its neighbors. The CCOS
detection part of the algorithm is limited to networks that are deployed in 2D Euclidean spaces, and nodes need to know
their own positions. The position information need not be highly accurate. The proposed algorithm is an extension of
our previous work [5], which partially examined the DOS detection problem. |
Notice that all the aforementioned research on the capacity of mobile ad hoc networks assumes global mobility, i.e.,
nodes can move around the whole network. However, this might not always be the case because in many situations
nodes only move within a limited region. For example, in a wireless network covering a big city, each network user
usually only moves around a small area close to his or her home, including the work place, groceries, restaurants, and
so on. As another example, consider a wireless network in a battlefield. Soldiers are not allowed to move around the
whole battlefield. Instead, they can only move in their own post areas in the battlefield. In the literature, Mammen and
Shah study in the throughput capacity under a restricted mobility model, where each node is allowed to move along a
randomly chosen great circle on the unit sphere with a uniform stationary distribution along the great circle. They show
that a constant per-node throughput can be achieved with a delay. In this paper, we investigate the throughput capacity
under a more practical restricted random mobility model, and attempt to provide a smooth trade-off between throughput and delay to fill the big gap existing in the literature Moreover, we notice that in the literature the capacity of wireless
networks is usually studied either in a dense network or in an extended network. In this study, we also explore the
impact of network size on the capacity and delay in the network. In particular, we consider a network of area n, where 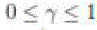 , and show that network size does not change the capacity and delay bounds in the network. , and show that network size does not change the capacity and delay bounds in the network. |
DISTRIBUTED CUT DETECTION |
Definitions and Problem Formulation |
| The problem we seek to address is twofold. First, we want to enable every node to detect if it is disconnected from the
source (i.e., if a DOS event has occurred). Second, we want to enable nodes that lie close to the cuts but are still
connected to the source (i.e., those that experience CCOS events) to detect CCOS events and alert the source node.
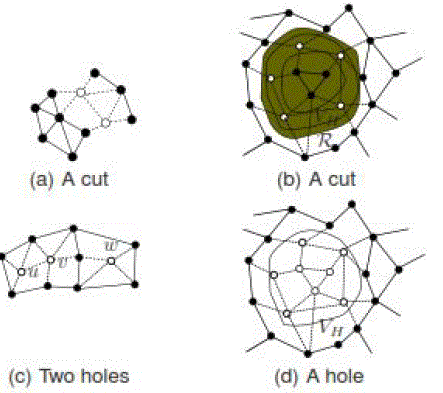
There is an algorithm-independent limit to how accurately cuts can be detected by nodes still connected to the source,
which are related to holes. Figure 1 provides a motivating example. This is discussed in detail in the Supplementary
Material, including formal definitions of “hole” etc. We therefore focus on developing methods to distinguish small
holes from large holes/cuts. We allow the possibility that the algorithm may not be able to tell a large hole (one whose circumference is larger than `from a
cut, since the examples of Figure 1(b) and (c) show that it may be impossible to distinguish between them. Note that
the discussion on hole detection part is limited to networks with nodes deployed in 2D. |
State update law and electrical analogy |
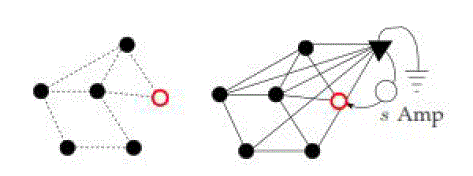
| The DCD algorithm is based on the following electrical analogy. Imagine the wireless sensor network as an electrical
circuit where current is injected at the source node and extracted out of a common fictitious node that is connected to
every node of the sensor network. Each edge is replaced by a 1Ω resistor. When a cut separates certain nodes from the
source node, the potential of each of those nodes becomes 0, since there is no current injection into their component.
The potentials are computed by an iterative scheme (described in the sequel) which only requires periodic
communication among neighboring nodes. The nodes use the computed potentials to detect if DOS events have
occurred (i.e., if they are disconnected from the source node). To detect CCOS events, the algorithm uses the fact that
the potentials of the nodes that are connected to the source node also change after the cut. However, a change in a
node’s potential is not enough to detect CCOS events, since failure of nodes that do not cause a cut also leads to
changes in the potentials of their neighbors. Therefore, CCOS detection proceeds by using probe messages that are
initiated by certain nodes that encounter failed neighbors, and are forwarded from one node to another in a way that if a
short path exists around a “hole” created by node failures, the message |
The Distributed Cut Detection (DCD) Algorithm |
DOS detection |
The approach here is to exploit the fact that if the state is close to 0 then the node is disconnected from the source,
otherwise not (this is made precise in Theorem 1 of Section . In order to reduce sensitivity of the
algorithm to variations in network size and structure, we use a normalized state. DOS detection part consists of steadystate
detection, normalized state computation, and connection/separation detection. Every node i maintains a binary variable 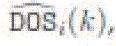 (k), which is set to 1 if the node believes it is disconnected from the source and
0 otherwise. This variable, which is called the DOS status, is initialized to 1 since there is no reason to believe a node is
connected to the source initially. A node keeps track of the positive steady states seen in the past using the following method. Each node I computes the normalized state difference (k), which is set to 1 if the node believes it is disconnected from the source and
0 otherwise. This variable, which is called the DOS status, is initialized to 1 since there is no reason to believe a node is
connected to the source initially. A node keeps track of the positive steady states seen in the past using the following method. Each node I computes the normalized state difference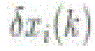 ) as follows: ) as follows: |
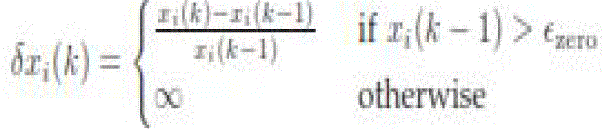 |
where 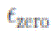 is a small positive number. A node i keeps a Boolean variable PSSR (Positive Steady State Reached) and
updates PSSR(k) ← 1 if is a small positive number. A node i keeps a Boolean variable PSSR (Positive Steady State Reached) and
updates PSSR(k) ← 1 if 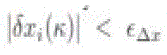  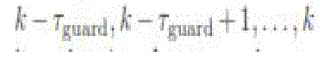 consecutive iterations), where consecutive iterations), where 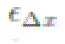 is a small positive number and is a small positive number and 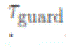 is a small integer. The initial 0 value of the state is not considered
a steady state, so PSSR(k) = 0 for is a small integer. The initial 0 value of the state is not considered
a steady state, so PSSR(k) = 0 for 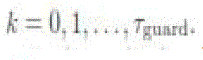 |
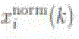 |
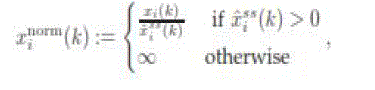 |
where ˆ  is the last steady state seen by i at k, i.e., the last entry of the vector is the last steady state seen by i at k, i.e., the last entry of the vector 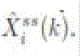 |
If the normalized state of I is less than 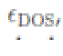 , where , where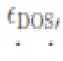 is a small positive number, then the node declares a cut has
taken place: is a small positive number, then the node declares a cut has
taken place: |
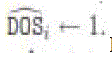 If the normalized state is If the normalized state is  meaning no steady state was seen until k, then meaning no steady state was seen until k, then 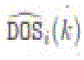 is set to 0 if the state
is positive and 1 otherwise. is set to 0 if the state
is positive and 1 otherwise. |
CCOS detection: |
The algorithm for detecting CCOS events relies on finding a short path around a hole, if it exists, and is partiallinspired
by the jamming detection algorithm proposed in [6]. The method utilizes node states to assign the tasof hole-detection
to the most appropriate nodes. Whea node detects a large change in its local state as well afailure of one or more of its
neighbors, and both of thesevents occur within a (predetermined) small time interval, the node initiates a PROBE
message. The pseudocode for the algorithm that decides when to initiate probe is included in Section of the
SupplementarMaterial. Each PROBE message p contains the following information: (i) a unique probe ID, (ii) probe
centroid C (seAlgorithm PROBE INITIATION in the SupplementarMaterial), (iii) destination node, (iv) path traversed
(ichronological order), and (v) the angle traversed by thprobe around the centroid. The probe is forwarded in manner
such that if the probe is triggered by the creatioof a small hole or cut (with circumference less than ` the probe traverses
a path around the hole in a counterclockwise (CCW) direction and reaches the node thainitiated the probe. In that case, the net angle traversed by the probe is 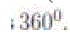 On the other hand, if the probe wainitiated by the occurrence of a
boundary cut, even if thprobe eventually reaches its node of initiation, the neangle traversed by the probe is 0. Nodes
forward a probonly if the distance traveled by the probe (the number ohops) is smaller than a threshold value There for
if a probe is initiated due to a large internal cut/holethen it will be absorbed by a node (i.e., not forwarded because it
exceeded the distance threshold constraint)and the absorbing node declares that a CCOS event hataken place. Details
on when the source node is alerted about the occurrence of a cut in the network is included in the Supplementary
Material. Max The information required to compute and update thesprobe variables necessitates the following
assumption for CCOS detection: On the other hand, if the probe wainitiated by the occurrence of a
boundary cut, even if thprobe eventually reaches its node of initiation, the neangle traversed by the probe is 0. Nodes
forward a probonly if the distance traveled by the probe (the number ohops) is smaller than a threshold value There for
if a probe is initiated due to a large internal cut/holethen it will be absorbed by a node (i.e., not forwarded because it
exceeded the distance threshold constraint)and the absorbing node declares that a CCOS event hataken place. Details
on when the source node is alerted about the occurrence of a cut in the network is included in the Supplementary
Material. Max The information required to compute and update thesprobe variables necessitates the following
assumption for CCOS detection: |
Assumption 1: |
i) The sensor network is a twodimensional geometric graph, with 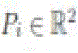 denoting the location of the
i-th node in a common Cartesian referenc frame; ii) Each node knows its own location as well athe locations of its
neighbors. denoting the location of the
i-th node in a common Cartesian referenc frame; ii) Each node knows its own location as well athe locations of its
neighbors. |
| The location information needed by the nodes need not be precise, since it is only used to compute destinations of
probe messages. The assumption of the network being 2D is needed to be able to define CW or CCW direction
unambiguously, which is used in forwarding probes. At the beginning of an iteration, every node starts with a list of
probes to process. The list of probes is the union of the probes it received from its neighbors and the probe it decided to
initiate, if any. The manner in which the information in each of the probes in its list is updated by a node is described in
Section of the Supplementary Material. |
AMULTIHOP RELAY SCHEME |
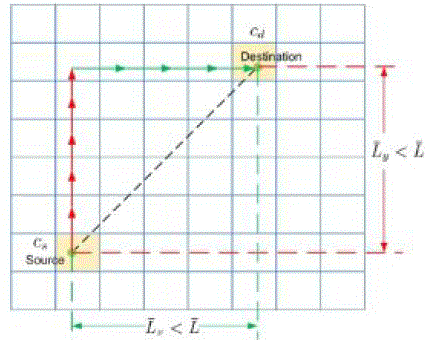
Before we move on with our main results, we first present a new multihop relay scheme for the transmissions between
source-destination pairs. S-I. Each square in the network becomes active in every 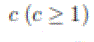 time slots. According to
the mobility model, in each time slot every node moves a distance of time slots. According to
the mobility model, in each time slot every node moves a distance of 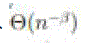 at a speed of at a speed of 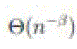 .So the length of a time slot is set to be The value of c will be determined later. .So the length of a time slot is set to be The value of c will be determined later. |
S-II. A node in an active square can transmit its packet to another node only if they are in the same square or in two
adjacent squares. Specifically, each time slot is further divided into three subslots A, B, and C, of the same length. For
a square with N nodes, each subslot is further divided into N minislots of the same length. . In subslot A, if 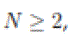 every node acting as source transmits one-by-one in a minislot its packet to another randomly chosen node in the same
square, which acts as a relay. This relay node can also be a destination node. In subslot B, if this active square is an
interior square, nothing happens. Otherwise, if this active square is on the boundary of a cell, every node in this square
acting as a relay transmits one-by-one in a minislot its packet to another randomly chosen node in the adjacent square
in the adjacent cell, which also acts as a relay. This relay node can also be a destination node. In subslot C, if every node acting as source transmits one-by-one in a minislot its packet to another randomly chosen node in the same
square, which acts as a relay. This relay node can also be a destination node. In subslot B, if this active square is an
interior square, nothing happens. Otherwise, if this active square is on the boundary of a cell, every node in this square
acting as a relay transmits one-by-one in a minislot its packet to another randomly chosen node in the adjacent square
in the adjacent cell, which also acts as a relay. This relay node can also be a destination node. In subslot C, if 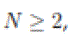 every node acting as a relay transmits one-by-one in a minislot its packet to the destination node if it is in the same
square. Otherwise, nothing happens. In other words, after receiving a packet from a source node in the same cell, a
relay node carries this packet and moves around until it goes to the boundary of the cell, where this relay node forwards
the packet to another node in an adjacent cell. Thus, a packet is transmitted at least once and at most twice in each of
the cells it goes through every node acting as a relay transmits one-by-one in a minislot its packet to the destination node if it is in the same
square. Otherwise, nothing happens. In other words, after receiving a packet from a source node in the same cell, a
relay node carries this packet and moves around until it goes to the boundary of the cell, where this relay node forwards
the packet to another node in an adjacent cell. Thus, a packet is transmitted at least once and at most twice in each of
the cells it goes through |
Throughput Capacity and Mobility |
We first derive an upper bound on the throughput capacity for all the schemes satisfying assumptions (A1) and (A2).
Recall that a transmission is considered to be successful if the Protocol Model is satisfied. Suppose that 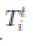 transmit and transmit and 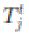 , respectively, at the same time t. Then, we have , respectively, at the same time t. Then, we have 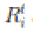 and and 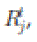 |
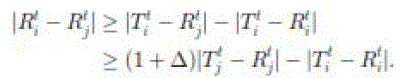 |
Average Packet Delay and Mobility |
We ignore the transmission time of the packets, since the transmissions are carried out at a much smaller time scale
than the nodes’ mobility. We also ignore the queuing delay as in [31]. In this study, we mainly focus on the delay
caused by nodes’ random mobility. We define three kinds of cells. A cell in which the source node of a packet is
located is called a Source Cell. A cell which
the destination node of a packet lies in is called a Destination Cell. The other cells which a packet goes through are
called Relay Cells., we have proved that when 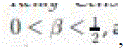 a square has at least two nodes with probability 1. Thus,
a source node can always find a relay node. Denote the time needed for the relay node in source cell to first hit a
boundary square by T square instead of a torus with size n S . Note that a cell is a a square has at least two nodes with probability 1. Thus,
a source node can always find a relay node. Denote the time needed for the relay node in source cell to first hit a
boundary square by T square instead of a torus with size n S . Note that a cell is a 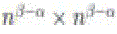 . Thus, due to which
approaches to 1 as . Thus, due to which
approaches to 1 as 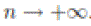 So, a packet can be relayed between cells successfully with high probability. Let So, a packet can be relayed between cells successfully with high probability. Let 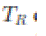 denote the time spent in each relay cell, and denote the time spent in each relay cell, and 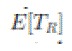 the expectation. Notice that Lemma 4 gives the expected the expectation. Notice that Lemma 4 gives the expected 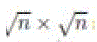 first hitting time when n nodes are uniformly distributed in squares, while in a relay cell, a node needs to
hit a boundary from the opposite boundary. Since [23] shows that the travel time increases as the distance, the expected
boundary hitting time in a relay cell is lower bounded by the expected first hitting time defined before, i.e., first hitting time when n nodes are uniformly distributed in squares, while in a relay cell, a node needs to
hit a boundary from the opposite boundary. Since [23] shows that the travel time increases as the distance, the expected
boundary hitting time in a relay cell is lower bounded by the expected first hitting time defined before, i.e., |
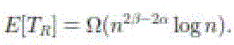 |
Trade-Offs among Capacity, Delay, and Mobility |
Recall that two parameters 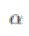 and and 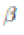 together define mobility pattern, and together define mobility pattern, and 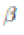 also defines a lower bound on the
transmission range. In Theorem 1, we observe that in order to obtain higher throughput, we need to increase also defines a lower bound on the
transmission range. In Theorem 1, we observe that in order to obtain higher throughput, we need to increase 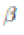 while
decreasing while
decreasing 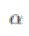 , which means that we need to allow nodes move in a larger area while have a smaller transmission
range. However, by doing this, the delay will also increase as the throughput increases, as we can find in Theorem As a
result, obviously, there are trade-offs among capacity, delay, and mobility. , which means that we need to allow nodes move in a larger area while have a smaller transmission
range. However, by doing this, the delay will also increase as the throughput increases, as we can find in Theorem As a
result, obviously, there are trade-offs among capacity, delay, and mobility. |
| Then, the exponential order of the upper bound on the expected average packet delay is This work was partially
supported by the US National Science Foundation under grants CNS-0916391, CNS0716450, CNS-0721744, and CNS-
1147813/1147851, and the China 111 Project under grant B08038. The work of J. Li was also partially supported by
Grand-in-Aid for Scientific Research from the Japan Society for Promotion of Science and Technology (JSPS), the
Okawa Foundation for Information and Telecommunications. The work of X. Huang was also partially supported by
the National Natural Science Foundation of China under grant 60903192 and the National High Technology Research
and Development Program of China (863 Program) under grant 2011AA010503. An earlier version of this paper was
presented at INFOCOM 2010 [19]. |
CONCLUSION |
Mobile ad hoc networks have been proved to be able to provide nondiminishing per-node throughput even when the
number of nodes in the network goes to infinity. However, the price to pay is that the end-to-end delay in the network is
very high, on the order of _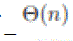 with possible logarithmic factors. Thus, we can only have either very low throughput, with possible logarithmic factors. Thus, we can only have either very low throughput,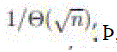 and short delay and short delay 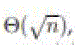 , in static ad hoc networks, or much higher throughput, , in static ad hoc networks, or much higher throughput,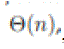 and much longer
delay, and much longer
delay, 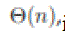 in mobile ad hoc networks. There is a big gap between the two extremes, which gives rise to an interesting
question: how can we fill the gap? This question is surely a valid question. In some scenarios, we do not need high
throughput, but have a strict requirement on delay. For example, in a tactical network, we may only exchange limited
and encrypted information once in a while to reduce the chance of being eavesdropped. But the information we deliver
is expected to be received in time. In other cases, we expect high throughput, but can tolerant a reasonable length of
delay. A delay tolerant network (DTN) or a social network can be such an example. Aiming at addressing the above
question, in this paper, we propose a new multihop relaying scheme, and investigate the throughput, delay, and
mobility in wireless ad hoc networks. Instead of global mobility, we consider a more practical restricted random
mobility model, and find that we can provide smooth trade-offs between throughput and delay in mobile ad hoc
networks by controlling nodes’ mobility pattern in mobile ad hoc networks. There is a big gap between the two extremes, which gives rise to an interesting
question: how can we fill the gap? This question is surely a valid question. In some scenarios, we do not need high
throughput, but have a strict requirement on delay. For example, in a tactical network, we may only exchange limited
and encrypted information once in a while to reduce the chance of being eavesdropped. But the information we deliver
is expected to be received in time. In other cases, we expect high throughput, but can tolerant a reasonable length of
delay. A delay tolerant network (DTN) or a social network can be such an example. Aiming at addressing the above
question, in this paper, we propose a new multihop relaying scheme, and investigate the throughput, delay, and
mobility in wireless ad hoc networks. Instead of global mobility, we consider a more practical restricted random
mobility model, and find that we can provide smooth trade-offs between throughput and delay in mobile ad hoc
networks by controlling nodes’ mobility pattern  In addition, currently we only consider network delay when
analyzing the trade-offs between throughput and delay. We will take queuing delay into consideration in our future
work. In addition, currently we only consider network delay when
analyzing the trade-offs between throughput and delay. We will take queuing delay into consideration in our future
work. |
| |
Figures at a glance |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References |
- S. Aeron and V. Saligrama, “Wireless Ad Hoc Networks: Strategies and Scaling Laws for the Fixed SNR Regime,” IEEE Trans. InformationTheory, vol. 53, no. 6, pp. 2044-2059, June 2007.
- Agarwal and P. Kumar, “Capacity Bounds for Ad Hoc and Hybrid Wireless Networks,” ACM SIGCOMM Computer Comm. Rev., vol. 34, no.3, pp. 71-81, July 2004.
- Buraagohain, S. Suri, C. Toth, and Y. Zhou, “Improved Throughput Bounds for Interference-Aware Routing in Wireless Networks,” Proc.Computing and Combinatorics (COCOON ’07), July 2007.
- Chen and E. Gunes, “On the Cover Time of Random Geometric Graphs,” Proc. Int’l Colloquium on Automata, Languages and Programming,July 2005.
- O. Dousse, M. Franceschetti, and P. Thiran, “On the Throughput Scaling of Wireless Relay Networks,” IEEE Trans. Information Theory, vol. 52,no. 6, pp. 2756-2761, June 2006.
- E. Duarte-Melo, A. Josan, M. Liu, D. Neuhoff, and S. Pradhan, “The Effect of Node Density and Propagation Model on Throughput Scaling ofWireless Networks,” Proc. IEEE Int’l Symp. Information Theory (ISIT ’06), July 2006.
- M. Franceschetti, O. Dousse, D.N. Tse, and P. Thiran, “Closing the Gap in the Capacity of Wireless Networks via Percolation Theory,” IEEETrans. Information Theory, vol. 53, no. 3, pp. 10091018, Mar. 2007.
- Gamal, J. Mammen, B. Prabhakar, and D. Shah, “ThroughputDelay Trade-Off in Wireless Networks,” Proc. IEEE INFOCOM, Mar. 2004.
- Gamal, J. Mammen, B. Prabhakar, and D. Shah, “Throughput- Delay Trade-Off in Wireless Networks—Part I: The Fluid Model,” IEEE Trans. Information Theory, vol. 52, no. 6, pp. 2568-2592, June 2006.
- Gamal, J. Mammen, B. Prabhakar, and D. Shah, “ThroughputDelay Trade-Off in Wireless Networks—Part II: Constant-Size Packets,” IEEE Trans. Information Theory, vol. 52, no. 11, pp. 51115116, Nov. 2006.
- M. Grossglauser and D. Tse, “Mobility Increases the Capacity of Ad Hoc Wireless Networks,” IEEE/ACM Trans. Networking, vol. 10, no. 4, pp. 477-486, Aug. 2002.
- P. Gupta and P. Kumar, “The Capacity of Wireless Networks,” IEEE Trans. Information Theory, vol. 46, no. 2, pp. 388-404, Mar. 2000.
- P. Gupta and P. Kumar, “Internets in the Sky: The Capacity of Three Dimensional Wireless Networks,” Comm. in Information and Systems, vol. 1, pp. 33-50, 2001.
- [14] C. Hu, X. Wang, and F. Wu, “Motioncast: On the Capacity and Delay Tradeoffs,” Proc. ACM MobiHoc, May 2009.
- D. Knuth, The Art of Computer Programming. Addison-Wesley, 1998.
- U. Kozat and L. Tassiulas, “Throughput Capacity of Random Ad Hoc Networks with Infrastructure Support,” Proc. ACM MobiCom, June 2003.
- P. Li and Y. Fang, “Impacts of Topology and Traffic Pattern on Capacity of Hybrid Wireless Networks,” IEEE Trans. Mobile Computing, vol. 8, no. 12, pp. 1585-1595, Dec. 2009. 438 IEEE TRANSACTIONS ON MOBILE COMPUTING, VOL. 11, NO. 3, MARCH 2012
- P. Li and Y. Fang, “The Capacity of Heterogeneous Wireless Networks,” Proc. IEEE INFOCOM, Mar. 2010.
- P. Li, Y. Fang, and J. Li, “Throughput, Delay, and Mobility in Wireless Ad Hoc Networks,” Proc. IEEE INFOCOM, Mar. 2010.
- P. Li, X. Huang, and Y. Fang, “Capacity Scaling of Multihop Cellular Networks,” Proc. IEEE INFOCOM, Apr. 2011.
- P. Li, M. Pan, and Y. Fang, “The Capacity of Three-Dimensional Wireless Ad Hoc Networks,” Proc. IEEE INFOCOM, Apr. 2011.
- P. Li, C. Zhang, and Y. Fang, “Capacity and Delay of Hybrid Wireless Broadband Access Networks,” IEEE J. Selected Areas in Comm., vol. 27, no. 2, pp. 117-125, Feb. 2009.
- X. Lin, G. Sharma, R. Mazumdar, and N. Shroff, “Degenerate Delay-Capacity Tradeoffs in Ad-Hoc Networks with Brownian Mobility,” IEEE/ACM Trans. Information Theory, vol. 52, no. 6, pp. 2777-2784, June 2006.
- X. Lin and N.B. Shroff, “The Fundamental Capacity-Delay Tradeoff in Large Mobile Ad Hoc Networks,” Proc. Third Ann.Mediterranean AdHoc Networking Workshop (MedHoc ’04), June 2004.
- Liu, Z. Liu, and D. Towsley, “On the Capacity of Hybrid Wireless Networks,” Proc. IEEE INFOCOM, Mar. 2003.
- Liu, P. Thiran, and D. Towsley, “Capacity of a Wireless Ad Hoc Network with Infrastructure,” Proc. ACM MobiHoc, Sept. 2007.
- J. Mammen and D. Shah, “Throughput and Delay in Random Wireless Networks with Restricted Mobility,” IEEE Trans. Information Theory, vol. 53, no. 3, pp. 1108-1116, Mar. 2007.
- R. Moraes, H. Sadjadpour, and J. Garcia-Luna-Aceves, “On Mobility-Capacity-Delay Trade-Off in Wireless Ad Hoc Networks,” Proc. IEEE/ACM 12th Ann. Int’l Symp. Modeling, Analysis, and Simulation of Computer and Telecomm. Systems (MASCOTS ’04), Oct. 2004.
- M. Neely and E. Modiano, “Capacity and Delay Tradeoffs for AdHoc Mobile Networks,” IEEE Trans. Information Theory, vol. 51, no. 6, pp. 1917-1937, June 2005.
- Ozgur, O. Leveque, and D. Tse, “Hierarchical Cooperation Achieves Optimal Capacity Scaling in Ad Hoc Networks,” IEEE Trans. Information Theory, vol. 53, no. 10, pp. 3549-3572, Oct. 2007.
- G. Sharma, R. Mazumdar, and N. Shroff, “Delay and Capacity Trade-Offs in Mobile Ad Hoc Networks: A Global Perspective,” IEEE/ACM Trans. Networking, vol. 15, no. 5, pp. 981-992, Oct. 2007.
- S. Toumpis, “Capacity Bounds for Three Classes of Wireless Networks,” Proc. ACM MobiHoc, May 2004.
- S. Toumpis and A. Goldsmith, “Large Wireless Networks Under Fading, Mobility, and Delay Constraints,” Proc. IEEE INFOCOM, Mar. 2004.
- L. Ying, S. Yang, and R. Srikant, “Optimal Delay-Throughput Trade-Offs in Mobile Ad Hoc Networks,” IEEE Trans. Information Theory, vol. 54, no. 9, pp. 4119-4143, Sept. 2008.
- Zemlianov and G. Veciana, “Capacity of Ad Hoc Wireless Networks with Infrastructure Support,” IEEE J. Selected Areas in Comm., vol. 23, no. 3, pp. 657-667, Mar. 2005.
- X. Zhu, P. Li, Y. Fang, and Y. Wang, “Throughput and Delay in Cooperative Wireless Networks with Partial Infrastructure,” IEEE Trans. Vehicular Technology, vol. 58, no. 8, pp. 4620-4627, Oct. 2009.
|