Some Prime Labeling of Graph

Abstract

A graph G=(V(G), E(G)) with vertex set V is said to have a prime labeling if its vertices can be labeled with distinct positive integer 1,2,3 V such that for edge u v E(G), the labels assigned to u and v are relatively prime. A graph which admits prime labeling is called a prime graph. Graph labeling is an important area of research in Graph theory. There are many kinds of graph labeling such as graceful labeling, Magic labeling, Prime labeling, and other different labeling techniques. In this paper we discuss prime labeling for some graphs.

We also discuss prime labeling in the related of some graph operations namely cycle, path, crown, Fan, star and wheel graph.

Keywords

Labeling; Prime labeling; Prime labeling of path graph; Cycle graph; Crown graph; Fan graph; Star graph; Wheel graph

Introduction

In this article, we consider only finite simple undirected graph [1]. The graph G has vertex set V=V(G) and edge set E=E(G). The labeling of a graph G is an assigning of integers either to the vertices or edges or both subject to certain conditions. The notion of a prime labeling was introduced by Roger Entringer and was discussed in a paper [2] for notations and terminology, [3]. Many researchers have studied prime graph for example in Fu [4]. H has proved that the path Pn on n vertices is a prime graphhave proved that the Cn on n vertices is a prime graph [5]. We refer to have proved Edge Vertex Prime Labeling for Wheel, Fan and Friendship Graph [6]. have proved that wheel Wn is a prime graph [7]. have proved the prime labeling for some Fan related graphs [8]. For latest survey on graph labeling, we refer to [9] have proved the prime labeling for some cycle related graphs [10] have proved the Prime labeling for some fan related graphs. The following definitions and notations are used in main results [11].

Materials And Methods

• Let G = (V(G), E(G)) be a graph with p vertices. A bijection f: V(G) → {1, 2, … p} is called a prime labeling if for each edge e = {u, v} belongs to E, we have gcd{f(u), f(v)} =1. A graph which admits prime labeling is called a prime graph.

• A simple graph of ‘n’ vertices(n≥3) and n edges forming a cycle of length ‘n’ is called as a cycle graph. In a cycle graph, all the vertices are of degree is 2. By adding the path, the new vertices of v₁, v₂, … v _m, and the new graph G is denoted by C_n @P_m

• The crown graph on 2n vertices is an undirected graph with two set of vertices {u1, u2, … un} and {v1, v2, … v n} and with on edge from ui to vj whenever i ≠ j. By adding the path, the new vertices of w1, w2, … w m, and the new graph G is denoted by crown C_n @P_m

• The Friendship graph F n is a graph which consists of ⴄ −triangles with a common vertex. If V(G) = 2n+1 and E(G) = 3_n by adding the path, the new vertices of v₁, v₂, … v _m, and the new graph G is denoted by F _n @P_m

• The star graph S_n is special type of graph in which n-1 vertices have degree 1 and single vertex have n-1 degree. This look like n-1 vertex is connected to central vertex. A star graph wit total n vertex is termed as S_n. By adding the path, the new vertices of v₁, v₂, … v _m, and the new graph G is denoted by S_n @P_m

• The wheel graph W_n is obtained by joining all vertices of a cycle C_n to a further vertex is called center. If V(G) = n+1 and E(G) = 2n by adding the path, the new vertices of v1, v2, … v m, and the new graph G is denoted by W_n @P_m

• Gear graph G_n also known as a bipartite wheel graph is a wheel graph with a vertex added between each pair of adjacent vertices of the outer cycle. Gear graph G_n has 2r+1 vertices and 3r edges. By adding the path, the new vertices of w1, w2, … w m, and the new graph G is denoted by G_n @Pm

Results And Discussion

Theorem

The cycle and path graph are a prime graph. Then the graph Cn @ Pm prime labeling of the graph

Proof:

Let G be the graph obtained by joining cycle Cn and a path Pm, then the graph C_n @ P_m admit to prime labeling of the graph.

Let u1, u2, … un be the vertices of cycle C_n and v1, v2, … vn be the vertices of path P_m.

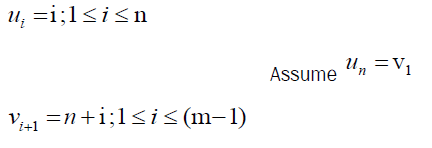
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, C_n @ P_m is a prime graph.

Figure 1: Prime labeling of graph C_n @ P_m

Prime labeling of graph C₄ @ P₆

The prime labeling of the graph is presented in the following graph.

Figure 2: Prime labeling of graph C₄ @ P₆

Theorem

The crown and path graph are a prime graph. Then the graph C_n @ P_m prime labeling of the graph

Proof:

Let G be the graph obtained by joining crown C_n by a path Pm admit to prime labeling of the graph.

Let u1, u2, … un be the vertices of crown C_n and v1, v2, … v_n be the vertices of cycle C_n, then

w1, w2, … w_n be the vertices of path Pm.

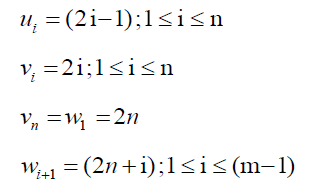
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, C_n @ P_m is a prime graph.

Figure 3: Prime labeling of crown graph C_n @ P_m

Prime labeling of graph crown C₃ @ P₄

The prime labeling of the graph is presented in the following graph.

Figure 4: Prime labeling of crown graph C₃ @ P₄

Theorem

The friendship and path graph are a prime graph. Then the graph F_n @ P_m prime labeling of the graph

Proof:

Let G be the graph obtained by joining friendship F_n by a path Pm admit to prime labeling of the graph.

Let u1, u2, … u_n be the vertices of friendship F_n and v1, v2, … v_n be the vertices of path P_m.

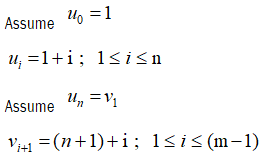
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, F_n @ P_m is a prime graph.

Figure 5: Prime labeling of graph F_n @ P_m

Prime labeling of graph F₃ @ P₆

The prime labeling of the graph is presented in the following graph.

Figure 6: Prime labeling of graph F₃ @ P₆

Theorem

The star and path graph are a prime graph. Then the graph S_n @ P_m prime labeling of the graph

Proof:

Let G be the graph obtained by joining star Sn by a path Pm admit to prime labeling of the graph.

Let u0, u1, u2, … u_n be the vertices of star Sn and v1, v2, … v_n be the vertices of path P_m.

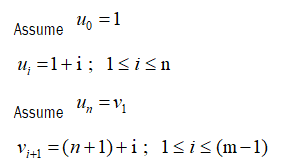
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, S_n @ P_m is a prime graph.

Figure 7: Prime labeling of star graph S_n @ P_m

Prime labeling of graph S₈ @ P₅

The prime labeling of the graph is presented in the following graph.

Figure 8: Prime labeling of star graph S₈ @ P₅

Theorem

The wheel and path graph are a prime graph. Then the graph W_n @ P_m prime labeling of the graph

Proof:

Let G be the graph obtained by joining wheel Wn by a path P_m, admit to prime labeling of the graph.

Let u0, u1, u2… u_n be the vertices of wheel Wn and v1, v2…v_n be the vertices of path P_m.

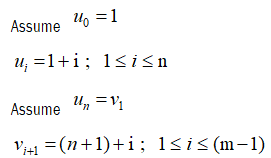
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, W_n @ P_m is a prime graph.

Figure 9: Prime labeling of graph W_n @ P_m

Prime labeling of graph W₆ @ P₅

The prime labeling of the graph is presented in the following graph

Figure 10: Prime labeling of wheel graph W₆ @ P₅

Theorem

The Gear and path graph are a prime graph. Then the graph G_n @ P_m prime labeling of the graph

Proof:

Let G be the graph obtained by joining Gear G_n by a path P_m.

Let u1, u2, …and v1, v2, …v_n be the vertices of Gear G_n and w1, w2, … w_n be the vertices path P_m.

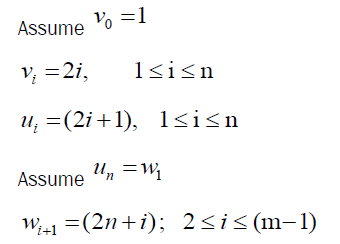
Clearly vertex labels are distinct.

Then f admits prime labeling. Thus, G_n @ P_m is a prime graph.

Figure 11: Prime labeling of graph G_n @ P_m

Prime labeling of graph G₆ @ P₅

The prime labeling of the graph is presented in the following graph.

Figure 12: Prime labeling of graph G₅ @ P₆

Conclusion

Prime labeling has been studied for then five decades. A huge number of research articles published in the area of graph theory and discrete mathematics. In this paper, we studied the prime labeling of some graph for, C_n@P_m, F_n@P_m, crown C_n@P_m, S_n@P_m and W_n@P_m, G_n@P_m in necessary conditions, In future work for some connected graphs.

References

1. Gallian JA. A Dynamic Survey of Graph Labeling. Electron J Comb. 2017

   [Google Scholar]

2. Tout A, et al. Prime labeling of Graphs, Nati Acada Sci Lett  1982;11:365-368.
3. Vaidya K, et al. Prime Labeling for Some Cycle Related Graphs. J Mat Res. 2010;23:98-104.

   [Google Scholar]

4. Lee SM et al. On the amalgamation of prime graphs. Bull Malays Math Sci Soc. 1988;11:59-67.
5. Bondy JA, et al. Graph theory with applications. Elsevier North Holland. New York. (1976).

   [Google Scholar]

6. Vaithilingam K. et al. Prime Labeling For Some Crown Related Graphs. Int J Sci. 2013;2.

   [Google Scholar]

7. Dretsky et al.  Vertex Prime labeling of graphs in graph theory. Combinatories and applications 1991;1:299-359. 
8. Meena S et al. Prime labeling for some fan related graphs. Int J Eng Res. Technol 2012;1
9. Parmar YM. Edge Vertex Prime Labeling for Wheel, Fan and Friendship Graph. Int  j math stat invent. 2017;5:23-29

   [Google Scholar]

10. H.C. Fu, et al. on Prime labeling Discrete Math 1994;127:181-186
11. Ramya N. et al. On Prime Labeling of some Classes of Graphs Int J Comput  Appl 2012;44:975-8887

    [Google Scholar]