1Department of Mathematics, Pondicherry University, Pondicherry, India
2Department of Mathematics, Vallam University, Tamil Nadu, India
Received: 03-Mar-2022, Manuscript No. JSMS-22-55261; Editor assigned: 07-Mar-2022, Pre QC No. JSMS-22-52261(PQ); Reviewed: 21-Mar-2022, QC No. JSMS-22-55261; Revised: 02-May-2022, Manuscript No. JSMS-22-55261 (R); Published: 17-May-2022, DOI: 10.4172/JSMS.8.5.006.
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
A graph G=(V(G), E(G)) with vertex set V is said to have a prime labeling if its vertices can be labeled with distinct positive integer 1,2,3 V such that for edge u v E(G), the labels assigned to u and v are relatively prime. A graph which admits prime labeling is called a prime graph. Graph labeling is an important area of research in Graph theory. There are many kinds of graph labeling such as graceful labeling, Magic labeling, Prime labeling, and other different labeling techniques. In this paper we discuss prime labeling for some graphs.
We also discuss prime labeling in the related of some graph operations namely cycle, path, crown, Fan, star and wheel graph.
Labeling; Prime labeling; Prime labeling of path graph; Cycle graph; Crown graph; Fan graph; Star graph; Wheel graph
In this article, we consider only finite simple undirected graph [1]. The graph G has vertex set V=V(G) and edge set E=E(G). The labeling of a graph G is an assigning of integers either to the vertices or edges or both subject to certain conditions. The notion of a prime labeling was introduced by Roger Entringer and was discussed in a paper [2] for notations and terminology, [3]. Many researchers have studied prime graph for example in Fu [4]. H has proved that the path Pn on n vertices is a prime graphhave proved that the Cn on n vertices is a prime graph [5]. We refer to have proved Edge Vertex Prime Labeling for Wheel, Fan and Friendship Graph [6]. have proved that wheel Wn is a prime graph [7]. have proved the prime labeling for some Fan related graphs [8]. For latest survey on graph labeling, we refer to [9] have proved the prime labeling for some cycle related graphs [10] have proved the Prime labeling for some fan related graphs. The following definitions and notations are used in main results [11].
Theorem
The cycle and path graph are a prime graph. Then the graph Cn @ Pm prime labeling of the graph
Proof:
Let G be the graph obtained by joining cycle Cn and a path Pm, then the graph Cn @ Pm admit to prime labeling of the graph.
Let u1, u2, … un be the vertices of cycle Cn and v1, v2, … vn be the vertices of path Pm.
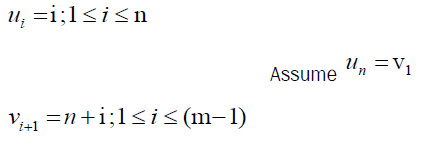
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, Cn @ Pm is a prime graph.
Prime labeling of graph C4 @ P6
The prime labeling of the graph is presented in the following graph.
Theorem
The crown and path graph are a prime graph. Then the graph Cn @ Pm prime labeling of the graph
Proof:
Let G be the graph obtained by joining crown Cn by a path Pm admit to prime labeling of the graph.
Let u1, u2, … un be the vertices of crown Cn and v1, v2, … vn be the vertices of cycle Cn, then
w1, w2, … wn be the vertices of path Pm.
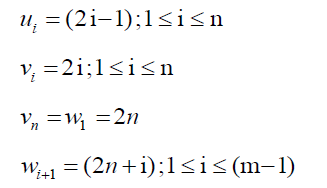
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, Cn @ Pm is a prime graph.
Prime labeling of graph crown C3 @ P4
The prime labeling of the graph is presented in the following graph.
Theorem
The friendship and path graph are a prime graph. Then the graph Fn @ Pm prime labeling of the graph
Proof:
Let G be the graph obtained by joining friendship Fn by a path Pm admit to prime labeling of the graph.
Let u1, u2, … un be the vertices of friendship Fn and v1, v2, … vn be the vertices of path Pm.
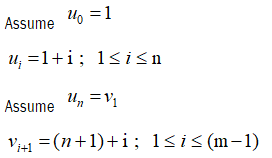
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, Fn @ Pm is a prime graph.
Prime labeling of graph F3 @ P6
The prime labeling of the graph is presented in the following graph.
Theorem
The star and path graph are a prime graph. Then the graph Sn @ Pm prime labeling of the graph
Proof:
Let G be the graph obtained by joining star Sn by a path Pm admit to prime labeling of the graph.
Let u0, u1, u2, … un be the vertices of star Sn and v1, v2, … vn be the vertices of path Pm.
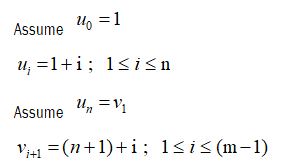
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, Sn @ Pm is a prime graph.
Prime labeling of graph S8 @ P5
The prime labeling of the graph is presented in the following graph.
Theorem
The wheel and path graph are a prime graph. Then the graph Wn @ Pm prime labeling of the graph
Proof:
Let G be the graph obtained by joining wheel Wn by a path Pm, admit to prime labeling of the graph.
Let u0, u1, u2… un be the vertices of wheel Wn and v1, v2…vn be the vertices of path Pm.
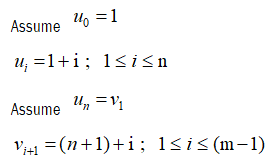
Clearly vertex labels are distinct. Then f admits prime labeling. Thus, Wn @ Pm is a prime graph.
Prime labeling of graph W6 @ P5
The prime labeling of the graph is presented in the following graph
Theorem
The Gear and path graph are a prime graph. Then the graph Gn @ Pm prime labeling of the graph
Proof:
Let G be the graph obtained by joining Gear Gn by a path Pm.
Let u1, u2, …and v1, v2, …vn be the vertices of Gear Gn and w1, w2, … wn be the vertices path Pm.
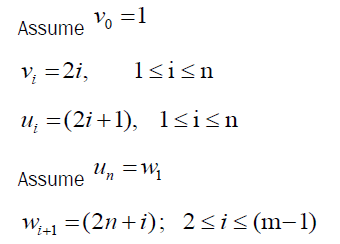
Clearly vertex labels are distinct.
Then f admits prime labeling. Thus, Gn @ Pm is a prime graph.
Prime labeling of graph G6 @ P5
The prime labeling of the graph is presented in the following graph.
Prime labeling has been studied for then five decades. A huge number of research articles published in the area of graph theory and discrete mathematics. In this paper, we studied the prime labeling of some graph for, Cn@Pm, Fn@Pm, crown Cn@Pm, Sn@Pm and Wn@Pm, Gn@Pm in necessary conditions, In future work for some connected graphs.