ISSN: 2319-9873
ISSN: 2319-9873
Rajagopal Reddy N, Sharief Basha S*
Department of Mathematics, Vellore Institute of Technology, Vellore, Tamil Nadu, India
Received: 12-Sep-2022, Manuscript No. JET-22-74304; Editor assigned: 14-Sep-2022, PreQC No. JET-22-74304 (PQ); Reviewed: 28-Sep-2022, QC No. JET-22-74304; Revised: 23-Jan-2023, Manuscript No. JET-22-74304 (R); Published: 31-Jan-2023, DOI: 10.4172/2319-9873.12.1.001
Citation: Basha SS, et al. The Energy of Hesitancy Fuzzy Graph. RRJ Eng Technol. 2023;12:001.
Copyright: © 2023 Basha SS, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
In this paper, the perception of the energy of the fuzzy graph is stretched to the energy of the Hesitancy Fuzzy Graph (HFG). We commit characterized the adjacency matrix of HFG and the energy of HFG is characterized regarding its adjacency matrix. The upper and lower boundaries are both derived for the hesitancy fuzzy graph’s energy.
Energy of a simple graph has been defined and many of its properties have been studied. In this paper, the concept of energy is extended to fuzzy graphs. Adjacency matrix of a fuzzy graph is defined and energy of a fuzzy graph is defined as the sum of absolute values of the eigenvalues of the adjacency matrix of the fuzzy graph.
Fuzzy set; Fuzzy graph; Hesitancy fuzzy set; Energy of hesitancy fuzzy graph; Zadeh’s
The FS was presented by Zadeh, whereas the fundamental part of the FS is merely a membership function. The FS is the generalization of Zadeh’s FS, which Atanassov introduced and defined by membership and nonmembership functions. The amount of membership and nonmembership degrees are equivalent to unity, in Zadeh’s FS. The amount of membership degree and a non-membership degree doesn’t surpass unity in Atanassov IFS. Many of the complications of the real world are highly complicated and involve ambiguous details. Further development for FSs was proposed by Torra V to calculate the lack of certainty and he called it as HFSs. HFSs are encouraged by some possible values to deal with the critical situation that develops when an element’s membership degree is fixed. While a specialist was requested to allocate various membership degrees with a group of x, y, z,? elements in a set A, this condition is frequently normal. Many complications occur due to unknown concerns and circumstances because one is accepted with hesitating times. The researcher required to develop the methods and means to deal with the problems. The HFS study and implementation were therefore carried on by researchers. HFSs have been applied to from several viewpoints, such as quantitative and qualitative [1].
The concept of Fuzzy Graphs (FGs) was introduced by Rosenfeld through a fundamental concept proposed by Kauffman, and some properties related to FGs were obtained. Bhattacharya explored the relationships between FGs and fuzzy groups and made some observations. A few works on FGs can also be found in Atanassov introduced the ideas of intuitionistic fuzzy relations and Intuitionistic Fuzzy Graph (IFG). Karunambigai and Parvathi established IFG and described operations between IFGs based on a specific instance of Atanassov’s concept. A few works on IFGs can also be found in Pathinathan, et al. proposed a new graph structure termed Hesitancy Fuzzy Graphs (HFGs) in 2015 and presented various fundamental principles connected to this structure. They didn’t assign Hesitant Fuzzy Elements (HFEs) to the nodes and paths of a graph. An intuitionistic fuzzy value instead of using HFEs were represented by three entries showing the degree of membership, the degree of hesitation, and the degree of membership of nodes and paths. The HFS concept and the IFS concept are similar, but they are fundamentally different based on how they are interpreted and used. In a decision making problem, the HFS is more useful than the IFS to model hesitancy in opinion about objects. Similarly, the HFG is a generalization of the IFG and FG, which is a more powerful tool than IFGs for representing a few decision making problems based on the uncertainty of decision makers relative to nodes and paths. Gutman I proposed the definition of graphs energy in 1978, as the amount of the complete estimations of the Eigen values of the adjacency matrix of the graph. Some energy limit are discussed in the energy of various graphs, namely regular, non-regular, circulate, and random graphs, are also being examined. For weighted graphs in and signed ones, energy is described. The graph’s energy is stretched out to the FG energy in E Kartheek and S Sharief basha defined some basic concepts on IFG energy and IFG Laplacian energy. The two boundaries of the IFG are discussed [2].
In this article, we describe the adjacency matrix of hesitancy fuzzy graph and the energy conception of the FG and IFG is generalized to the energy of the HFG. This article is arranged as follows. We stretch all the fundamental concepts relevant to FSs, HFSs, the energy of a graph, and the energy of FG in Section 2. The energy of the HFG is defined in section 3. There are also developed the lower and the upper limits for the energy of the HFG. We give the outcome in section 4.
Preliminaries
This section provides a brief introduction to HGF principles and terminologies as well as the energy for HFGs, which is required for the systematic review.
Let Y is a non-empty set. The FS-A in Y is denoted as A=(y,μA(y))/y ∈ Y which is considered by a membership function μA(y): Y→(0,1) and an FS satisfying the following condition, μA(y)+γA(y)=1 where γA(y)=1−μA(y) is the nonmembership function.
Let Y is the fixed set, and HFS on Y is in terms of a function that when extended to Y returns a subset of (0,1). To be certainly known, Xia and Xu (2011a) conveyed the HFS by a mathematical symbol:
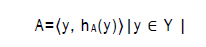
Where hA(y) is a set of some values in (0,1), indicating the possible membership degrees of the element y ∈ Y to the set. Xu and Xia called h=hA(y) is the Hesitant Fuzzy Element (HFE) and? The set of all HFEs.
A FG with vertices V as the underlying set is a pair of functions HG=(V,E,σ,μ) where σ: V→ (0,1) is a fuzzy subset and μ: V × V→ (0,1) is a symmetric fuzzy relation on the fuzzy subset? for all (u,v) ∈ V such that μ(u,v) ≤ σ(u) ∩ σ(v). The underlying crisp graph of HG=(σ,μ) is represented by HG=(V,E) where E ⊆ V × V.
A fuzzy relation matrix M=(mij), where mij=μ(vi,vj). If the fuzzy relation can also be conveyed by a matrix. Throughout this article, we assume that FG is undirected without loops and σ(v)=1 for each v ∈ V (Figure 1).
Let G=(σ,μ) be a FG with pnodes and q edges. The adjacency matrix of G=(σ,μ) be a square matrix of order p then A(G)=[aij] where aij=μ(vi,vj) entry is as the strength of the connection between the nodes vi and vj.
Let G? Is an FG represented in Figure 2 The adjacency matrix of the FG G1? Is

Let u is a vertex of the FG G=(σ,μ). The degree of u is as
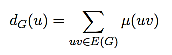
Let G=(σ,μ) is the FG on G=(V,E) of dG(v)=k ∀v∈V, then G is known a regular fuzzy graph of degree k [3].
Let G=(σ,μ) is the FG with p vertices and q edges. The degree matrix of G=(σ,μ) is a square matrix of order n whose D(G)=(dij) and we have
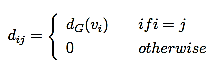
Suppose {λ1, λ2, . . . , λn} are the Eigenvalues of the fuzzy adjacency matrix A(G) with {λ1 ≥ λ2 ≥ · · · ≥ λn} then
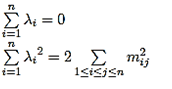
Let G be an FG with |V|=p vertices. The adjacency matrix of (G2) can be defined from the Figure 2.
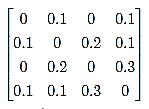
The spectrum of G2 is {−0.34,−0.1,0,0.44} we have also
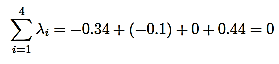
A HFG is of the form HG=(V,E,μ,γ,β) where
V={v1,v2,v3, . . . , vp} such that μ1?V→(0,1), γ1?V→(0,1) and β1?V→(0,1) denotes the membership, nonmembership degree and the degree of hesitancy of the element and μ1(vi)+γ1(vi)+β1(vi)=1∀ vi∈V, where
β1 (vi)=1−[μ1(vi)+γ1(vi)] (2.1)
E ⊆ V × V where μ2: V × V → (0,1), γ2: V × V→(0,1) and β2: V × V→(0,1) such that,
μ2(vi,vj) ≤ min [μ1(vi), μ1(vj)] (2.2)
γ2(vi,vj) ≤ max [γ1(vi),γ1(vj)] (2.3)
β2(vi,vj) ≤ max [β1(vi),β1(vj)] (2.4)
and
0 ≤ μ2(vi,vj)+γ2(vi,vj)+β2(vi,vj) ≤ 1, ∀ (vi,vj) ∈ E. (2.5)
In this example, we gained the new HFG graph with the above mentioned properties (Figure 3).
Consider G=(V,E), where V=a,b,c,d
Energy of hesitancy fuzzy graph
In this section, we describe the energy of a hesitancy fuzzy directed graph without loops. The connection construction of a site could be addressed by a directed HFG. The connections are considered as nodes and paths between the connections are considered as edges. The weightage of every edge is considered as the number of guests (membership value), the number of nonguests (non-membership value), and drop off (hesitancy fuzzy index) among that connections structure. The two upper and lower limits of the HFG?s energy are evaluated [4].
Consider HG=(V,E,μ,γ,β) is hesitancy fuzzy graph and A (HG) is hesitancy fuzzy adjacency matrix of HFG is defined as A(HG)=[rij] where rij=(μ(vi,vj), γ(vi,vj), β(vi,vj ), μ(vi,vj) is represents the relation of membership value between vi and vj, γ(vi,vj) is represents the relation of nonmembership value between vi and vj and β(vi,vj) is represents the relation of hesitant value between vi and vj [5,6].
The adjacency matrix of HFG, from Figure 3 is defined as
Consider HG=(V,E,μ,γ,β) is hesitancy fuzzy graph and the Hesitancy Fuzzy Adjacency Matrix (HFAM) of HFG is A(HG) can be defined as three matrices, one of the matrix containing the values as membership elements, second matrix containing the elements as nonmembership values and last matrix containing the elements as hesitant values which is denoted as
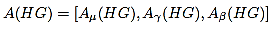
Where Aμ is the membership element matrix, Aγ is the nonmembership element matrix and Aβ is the hesitant element matrix
matrix
Now we define the three matrices Aμ(HG), Aγ(HG) and Aβ(HG) of HFG is
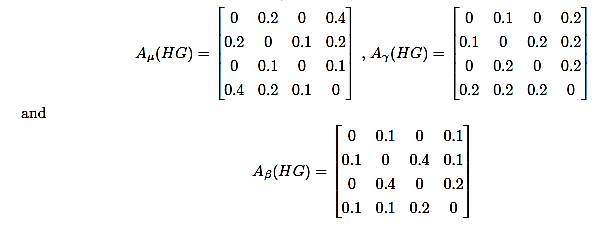
Consider HG=(V,E,μ,γ,β) is HFG and A(HG) is HFAM of HFG then the eigenroots of HFAM A(HG) is defined as (P,Q,R) where P is the set of eigenroot of membership element matrix Aμ(HG), Q is the set of eigenroots of membership element matrix Aγ(HG) and R is the set of eigenroots of membership element matrix Aβ(HG) [7-11].
Consider HG=(V,E,μ,γ,β) is HFG and A(HG) is HFAM then the energy of HFG is defined as E(HG) and denotes as
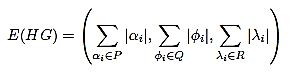
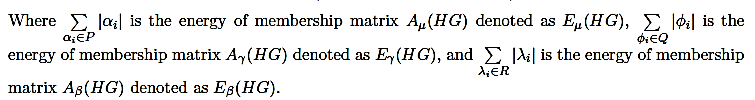
Now find the energy of HFG using the characteristic equation |A(HG)−λI|
The energy of membership function of HFG
The energy of membership function of hesitancy fuzzy graph is
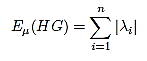
The adjacency matrix of Aμ(HG) is
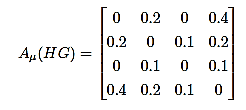
Now calculate the Eigen values of membership matrix Aμ(HG) using the characteristic equation |Aμ(HG)−λI|=0 is
λ1=−0.4129, λ2=−0.1651,
λ3=0.0103, λ4=0.5676
Now
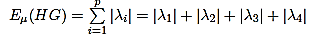
Substituting the calculated Eigen values of Aμ(HG) in above equation, we get
Eμ(HG)=|−0.4129|+|−0.1651|+|0.0103|+|0.5676|
By calculating we get the energy of membership matrix of HFAM of HFG is
Eμ(HG)=1.1559
The energy of nonmembership function of HFG
The energy of membership function of hesitancy fuzzy graph is
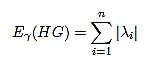
The adjacency matrix of Aγ(HG) is
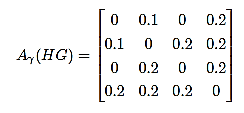
Now calculate the Eigen values of membership matrix Aγ(HG) using the characteristic equation |Aγ(HG)−λI|=0 is
λ1=−0.2835, λ2=−0.2000,
λ3=−0.0151, λ4=−0.4684
Now
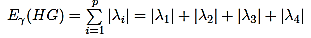
Substituting the calculated Eigen values of Aγ(HG) in above equation, we get
Eγ(HG)=|−0.2835|+|−0.2000|+|−0.0151|+|−0.4684|
By Calculating we get the energy of nonmembership matrix of HFAM of HFG is
Eγ(HG)=0.9670
The energy of nonmembership function of HFG
The energy of membership function of hesitancy fuzzy graph is
The adjacency matrix of Aβ(HG) is
Now calculate the Eigen values of membership matrix Aβ(HG) using the characteristic equation |Aβ(HG)−λI|=0 is
λ1=−0.4314, λ2=−0.1000,
λ3=0.0181, λ4=0.5314
Now
Substituting the calculated Eigen values of Aβ(HG) in above equation, we get
Eβ(HG)=|−0.4314|+|−0.1000|+|0.0181|+|0.5314|
By Calculating we get the energy of hesitant element matrix of HFAM of HFG is
Eβ(HG)=1.0809
Therefore, the energy of hesitancy fuzzy graph is
E(HG)=[Eμ(HG),Eγ(HG),Eβ(HG)]=[1.1623, 0.9670, 1.0809]
Let HG be an HFG (not having the loops) with |V|=p and |E|=q and A(HG)=((μij)(γij)(βij)) be Hesitancy fuzzy adjacency matrix of HFG HG then
Where |A| is the determinant of A(μij(HG))
Proof. By the conditions Cauchy?s Schwartz inequality to the p numbers 1, . . . , 1 and |λ1|, |λ2|, . . . , |λp|
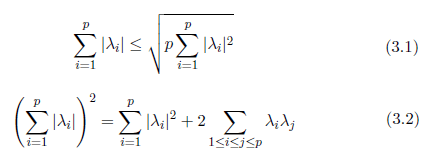
By the characteristic polynomial of the adjacency matrix A(HG) we have
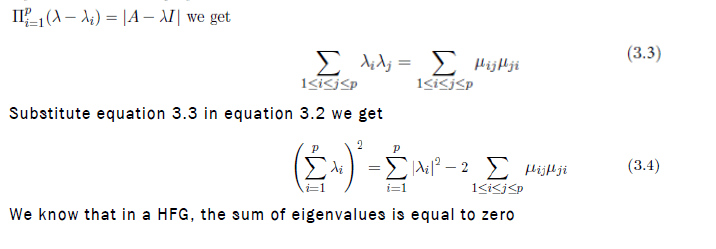
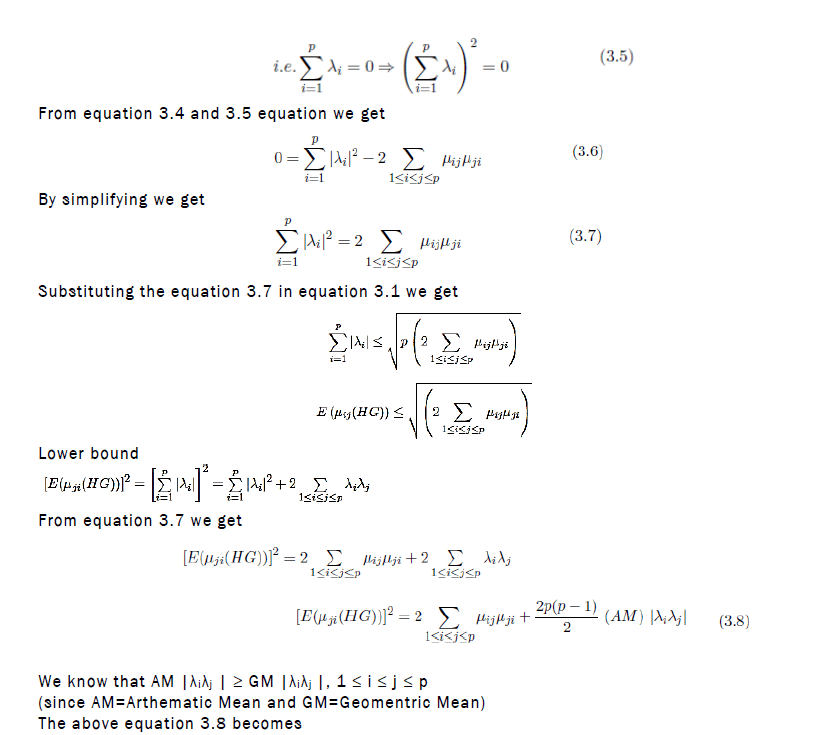
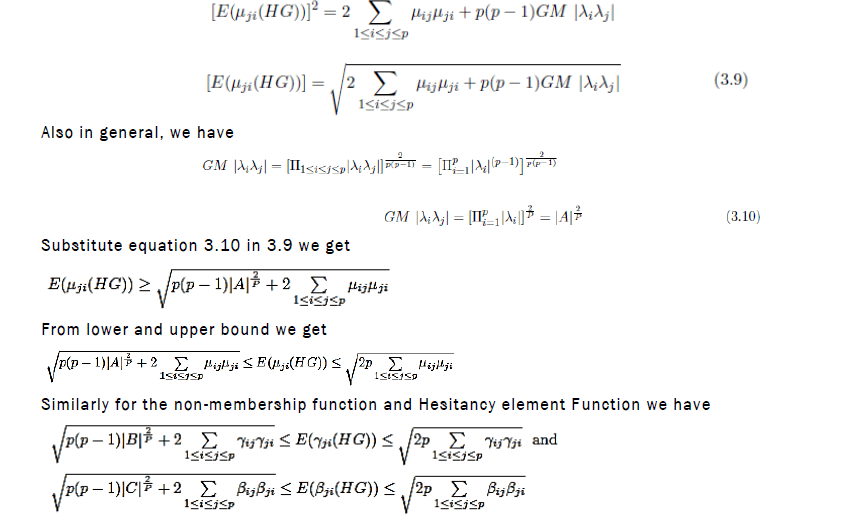
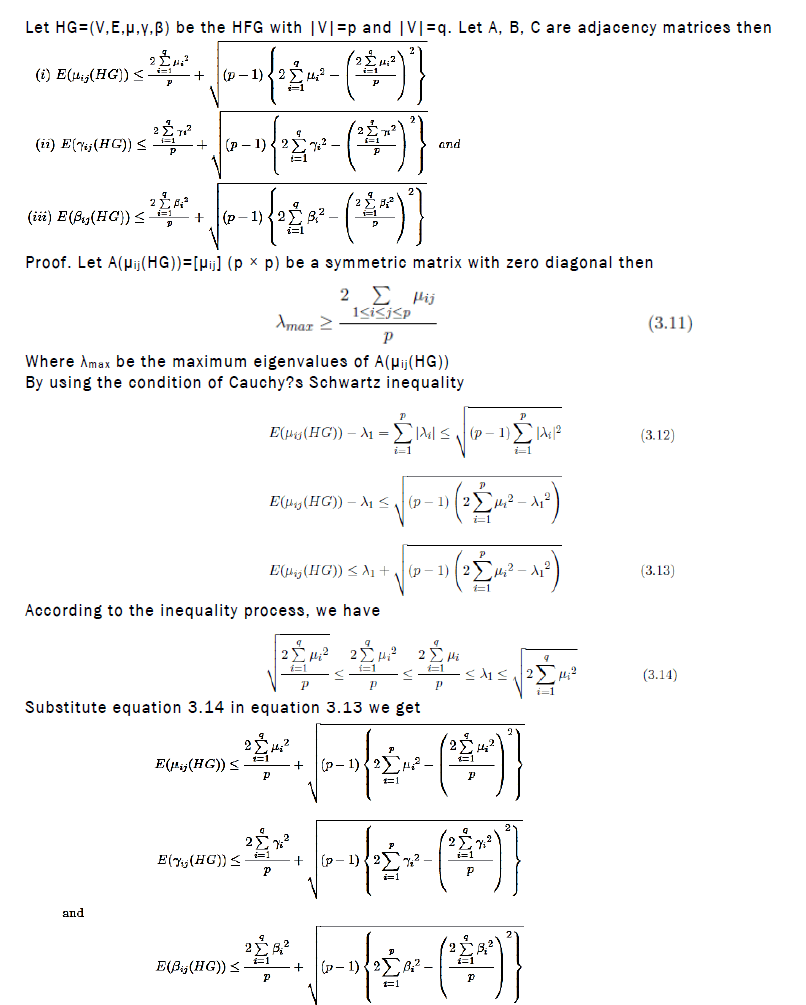
Example: (Illustration to theorem) we get
E(μ(HG))=1.1623, E(γ(HG))=0.9670 and E(β(HG))=1.0809.
We describe the adjacency matrix of hesitancy fuzzy graph and also defined the energy of a hesitancy fuzzy graph. The two upper and lower limits of energy of hesitancy fuzzy graph are extracted and verified with a suitable example. Some related outcomes have been examined and demonstrated.
[Crossref]
[Crossref] [Google Scholar] [PubMed]