The Synergistic Effect of La And Yb on the Microstructure and Mechanical Properties of Al-Cu-Mg Alloy

Abstract

The Al-4.6Cu-1.6Mg alloys with different contents of La and Yb were fabricated by ultrasonic assisted casting in this study. The synergistic effect of La and Yb additions on the microstructure and mechanical properties of Al-4.6Cu-1.6Mg alloys was systematically studied. The results showed that adding La and Yb into Al-4.6Cu-1.6Mg alloys had an obvious grain refining effect and could form new two phases of Al₆Cu₆La and Al_7.4Cu_9.6Yb₂. The Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy exhibited the optimal microstructure and mechanical properties. Compared to Al-4.6Cu-1.6Mg alloy, the grain was obviously refined. According to the calculated results, the grain refining effect was attributed to the heterogeneous nucleation and compositional undercooling. Additionally, the yield strength, ultimate tensile strength and elongation of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy were 181.2 MPa, 264.5 MPa and 6.3%, which were 41.2%, 45.1% and 75.0% higher than those of the unmodified alloy, respectively. The strength mechanisms of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy were ascribed to the refinement strengthening, solid solution strengthening and second phase strengthening, in which the refinement strengthening was the main strength mechanism.

Keywords

Microstructure; Mechanical properties; Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy; Grain refining; Strengthening mechanisms

Introduction

Due to their high strength, good machinability and excellent heat and damage resistance performance, Al-Cu-Mg alloys have been extensively used in aerospace industry and automobile manufacturing [1-3]. However, the application of casting Al-Cu-Mg alloys has been greatly limited because of the coarse second phases and dendritic structures [4,5].

Accordingly, in order to meet the increasingly strict manufacturing requirements, it is very necessary to further enhance comprehensive performance of Al-Cu-Mg alloys. It is well known that adding Rare Earth (RE) elements into aluminum alloys can significantly improve their microstructure and mechanical properties [6,7]. Up to now, a number of scholars have studied the effects of RE elements, such as La, Er, Ce, Sc, Y and Yb on the microstructure and mechanical properties of various aluminum alloys [8-13].

Specially, as the most economic light RE element, La has been attracted extensively attention and widely used in recent years. Zheng et al., investigated the effect of trace La addition on the α-Al grain and eutectic Si as well as mechanical properties of Al-Si alloys [14]. They observed that 0.06 wt.% La addition was sufficient to achieve the best modified effect for the microstructure and mechanical properties of the Al-Si alloys. And, they also concluded that La refined α-Al grain by reducing the wetting angle and modified the eutectic Si by changing the growth method of eutectic Si. Also demonstrated the similar effects on the refinement mechanism of the α-Al grains and modification behavior of the Al13Fe4 phase in the Al-Fe-La alloy [15]. Besides, they found that adding La into Al-Fe alloys could achieve simultaneous improvements of their strength and plasticity. Meanwhile, as one of the most effective heavy RE elements, Yb has also received widespread concerns. Wang et al., explored the influence of Yb addition on the microstructure and mechanical properties of Al-Ni alloy [16]. They indicated that trace Yb addition decreased the SDAS of α-Al grain and refined the Al3Ni phase, which resulted in the improvement of mechanical properties of the alloy. Xiong et al., reported the microstructure and mechanical properties of ADC12 alloy with different Yb additions [17]. The results showed that 0.8 wt.% Yb addition obtained the optimal mechanical properties, due to refining coarse α-Al dendrites and modifying the morphology of the β-Fe and eutectic Si phases.

As can be noted from the reported literature, the effects of La or Yb on the microstructure and mechanical properties of aluminum alloys were studied individually. Related study indicated that the modification effect of mixed RE was better than that of single RE, and mixed RE had a synergistic superposition [18]. However, as far as we know, there are few literature about the combined effect of La and Yb on the microstructure and mechanical properties of aluminum alloys, especially for Al-Cu-Mg alloys. Additionally, the refinement mechanisms of RE are complex and have still not formed unified conclusion yet. At present, the accepted refinement mechanisms of RE mainly include compositional undercooling and heterogeneous nucleation theories [18-22]. For heterogeneous nucleation theory, the formation of RE intermetallics can serve as effective nucleation substrates, which contributes to increase nucleation rate, thus refining α-Al grains. For compositional undercooling theory, RE atoms enrich at solid-liquid interface front during the solidification process, which can generate compositional undercooling and hinder the continuous growth of α-Al grains, thus refining the grains. However, whether the refinement mechanisms of La and Yb on Al-Cu-Mg alloys can be elaborated by the compositional undercooling or heterogeneous nucleation theories lack the in-depth study and need to be further confirmed. Moreover, the strengthening mechanisms of La and Yb on Al-Cu-Mg alloys are still unclear. Hence, it is necessary to study the combined effect of La and Yb on the microstructure and mechanical properties of Al-Cu-Mg alloys.

In this work, Al-4.6Cu-1.6Mg alloys with different contents of La and Yb were fabricated by ultrasonic assisted casting. And, the combined effect of La and Yb on the microstructure and mechanical properties of Al-4.6Cu-1.6Mg alloys was studied. Moreover, the refinement mechanisms of La and Yb on the α-Al grains were discussed in details. Furthermore, the strengthening mechanisms of La and Yb on Al-4.6Cu-1.6Mg alloys were quantitatively analyzed.

Materials and Methods

Materials preparation

In this experiment, Al-4.6Cu-1.6Mg alloys, Al-10% La and Al-10%Yb master alloys were used as raw materials. Firstly, Al-4.6Cu-1.6Mg alloys placing into graphite crucible were melted in a resistance furnace at 750°C. After degassing and removing the slag, the Al-10% La and Al-10% Yb master alloys wrapped by aluminum foil were added into melt. Then, the melt was held at 720°C for 30 min in order to ensure that the master alloys were completely melted. Next, the high-energy ultrasonic vibration with the ultrasonic power of 2.8 kW and ultrasonic frequency of 20 kHz was applied to the melt for 10 min. After removing the slag, the melt was poured in to a permanent metal mold preheated to 200°C. Finally, the Al-4.6Cu-1.6Mg alloys with different contents of La and Yb were obtained. Table 1 presents the chemical composites of the experimental alloys analyzed by Inductively Coupled Plasma-Atomic Emission Spectroscopy. During the whole experiment, argon gas was applied to protect the melt from oxidation as shown in Table 1.

Table 1. Chemical composites of the experimental alloys (wt.%).

Material characterization

The microstructure and fracture surfaces were characterized by scanning electron microscopy (SEM, Tescan-Vega3) equipped with Energy Dispersive X-ray Spectroscopy (EDS). The phase composition was identified by X-ray diffraction (XRD, D8 ADVANCE). The solidification behavior of the alloys was analyzed by differential scanning calorimeter (DSC, DSC404F3). The RE intermetallics in the Al-Cu-Mg-0.6 (La+Yb) were observed by transmission electron microscopy (TEM, TalosF200X). The mean diameter of α-Al phases and secondary dendrite arm spacing (SDAS) were measured by Image Pro Plus 6.0 software. The tensile samples were machined into tensile bars, which the gauge length was 40 mm and the diameter was 6 mm. The tensile tests were conducted on an UTM5105 machine at a strain rate of 0.001 s^-1. In order to guarantee the reliability of measure results, more than three samples were tested for each condition.

Results and Discussion

Microstructure

The microstructures of Al-4.6Cu-1.6Mg alloys with different contents of La and Yb are displayed in Figure 1. Without the addition of La and Yb, the coarse α-Al dendrites are clearly observed, as depicted in Figure 1a. As the La and Yb addition reaches 0.3 wt.%, the content of coarse α-Al dendrites significantly decreases (Figure 1b). When the La and Yb addition increases up to 0.6 wt.%, the mean diameter of α-Al phases become finest (Figure 1c). While the La and Yb addition continues to increase, the α-Al dendrites begin to become coarse, as displayed in Figure 1d.

Similarly, the change trend of SADS is the same as that of α-Al dendrites with different contents of La and Yb. The mean diameter of α-Al phases and SADS in the Al-4.6Cu-1.6Mg alloys with different contents of La and Yb are illustrated in Figure 2. It can be seen that La and Yb addition can achieve obviously grain refinement as shown in Figure 2.

The SEM image and EDS spectra of unmodified Al-4.6Cu-1.6Mg alloy are shown in Figure 3. It can be noted from Figure 3a that the microstructure of as-cast Al-4.6Cu-1.6Mg alloy is composed of α-Al matrix and grain boundary eutectic phases including block-shaped phase and grid-like phase. As depicted in Figure 3b, the EDS result reveals that the stoichiometry of block-shaped phase is 77.15 at.% Al and 22.85 at.% Cu. Combining with the XRD results, it can be seen that the block-shaped phase is Al2Cu phase. As exhibited in Figure 3c, the EDS result indicates that the stoichiometry of grid-like phase is 77.02 at.% Al, 12.44 at.% Cu, 10.54 at.% Mg, which is close to the stoichiometry of the Al₂CuMg phase. Thus, the microstructure of as-cast Al-4.6Cu-1.6Mg alloy mainly consists of α-Al matrix, Al₂Cu and Al₂CuMg phases as shown in Figure 3.

Besides the phases mentioned above, some new phases appear in the microstructure of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy. Figure 4 shows the SEM image and corresponding element mappings of the microstructure in Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy. It can be seen from Figures 4d-4f that the element distributions of Cu, La and Yb are almost the same. Combining XRD result and previous studies [23,24], new two kinds of phases of Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ may be formed in Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy. Based on the results of calculated formation enthalpies of infinite diluted solution, a strong interaction exists between Cu and La, Yb atoms [25,26], which shows that La, Yb and Cu atoms have favourable chemical affinity, thus resulting in that Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ phases may be formed when adding La and Yb into the Cu-containing aluminum alloy. Additionally, Mg element is basically dissolved in the α-Al matrix, as shown in Figure 4.

Figure 5 is XRD patterns of Al-4.6Cu-1.6Mg alloys with different contents of La and Yb. It can be observed that all alloys are mainly composed of α-Al matrix, Al2Cu and Al2CuMg phases. Compared to unmodified Al-4.6Cu-1.6Mg alloy, two kinds of new phases of Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ are observed in the modified alloys. And, the quantity of Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ phases increase with the increase of La and Yb addition as shown in Figure 5.

To further confirm the formation of Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ phases, a detailed TEM observation was conducted. Figure 6 illustrates the bright field TEM images, Selected Area Electron Diffraction (SAED) patterns, High-Resolution Transmission Electron Microscopy (HRTEM) images and EDS mapping analysis of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy. A irregular blocky particle with twin structure can be observed, as shown in Figure 6a. And, the average size of the particle is found to be ~1.5 μm. Based on the SAED pattern, it is observed that the diffraction spots are in accordance with the diffraction spots incident by Al_7.4Cu_9.6Yb₂ phase from the direction of [-14-4], as shown in Figure 6b. Therefore, the phase can be identified as Al_7.4Cu_9.6Yb₂ phase (trigonal system, a=b=0.8691 nm, c=1.2698 nm, with space group R-3m). As shown in the HRTEM image, the interplanar spacing of this phase is 0.43 nm, corresponding to the (110) crystal plane of Al_7.4Cu_9.6Yb₂ phase. According to the results of EDS mapping in Figures 6c-6h, the particle consists mainly of Al, Cu, La and Yb elements and the element distributions are almost the same, suggesting that the Al₆Cu₆La phase may be also formed in addition to forming Al_7.4Cu_9.6Yb₂ phase. According to relevant literature [26,27], the standard formation gibbs free energy of Al₆Cu₆La phase is more negative than that of Al_7.4Cu_9.6Yb₂ phase, resulting in that the order of ability to form Al₆Cu₆La phase is superior to that of Al_7.4Cu_9.6Yb₂ phase. Accordingly, the Al_7.4Cu_9.6Yb₂ phase is formed by covering on the Al₆Cu₆La phase, which makes the Al₆Cu₆La phase unable to be observed. A similar phenomenon was observed in the (Ce+Yb)-modified Al-6Si-0.6Mg-0.6Cu-0.2Cr cast alloy [28]. Additionally, some studies have shown that when adding minor RE elements into the alloy, RE atoms could substitute lattice atoms of particles and adsorb on the growing interface of primary phases, thus changing the growth direction and generating the twins [29,30]. Besides, plenty of high density dislocations exist near Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ particles, as shown in Figure 6a. This is due to the fact that Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ particles can hinder the dislocations motion, resulting in the dislocations pile-up ahead of these particles. The interaction between these particles and dislocations can lead to the second phase strengthening as shown in Figure 6.

The DSC curves of Al-4.6Cu-1.6Mg alloys with different contents of La and Yb are displayed in Figure 7. It can be observed that the DSC curves of all alloys contain three endothermic peaks (Peak1, Peak2 and Peak3). Peak1, Peak2 and Peak3 represent the melting temperatures of α-Al dendrites, Al2CuMg and Al2Cu phases, respectively as shown in Figure 7.

Table 2 presents the analysis results of DSC curves in Figure 7. It can be noted that adding La and Yb into Al-4.6Cu-1.6Mg alloys can decrease the nucleation undercooling of α-Al, which contributes to promoting the nucleation during the solidification process, thus refining the α-Al grain. It is worth noting that the enthalpy of Al2CuMg phase decreases when adding La and Yb into Al-4.6Cu-1.6Mg alloys, indicating that the number of Al2CuMg phase is reduced in the modified alloys as shown in Table 2.

Table 2. Results of DSC curves of Al-4.6Cu-1.6Mg alloys with different contents of La and Yb.

Mechanical properties

The mechanical properties of Al-4.6Cu-1.6Mg alloys with different contents of La and Yb are displayed in Figure 8. It can be noted that the yield strength, ultimate tensile strength and elongation of the alloys increase first and then decrease with increasing La and Yb addition. The unmodified alloy exhibits the lowest yield strength, ultimate tensile strength and elongation, which are 128.3 MPa, 182.3 MPa and 3.6%, respectively. While the Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy shows the optimal yield strength, ultimate tensile strength and elongation of 181.2 MPa, 264.5 MPa and 6.3%, which are 41.2%, 45.1% and 75.0% higher than those of the unmodified alloy, respectively as shown in Figure 8.

Q=UTS+??×log(EI)

Where UTS is the ultimate tensile strength, EI is the elongation and a is 150 MPa for Al-4.6Cu-1.6Mg alloys [31]. The Q value can better reflect the true mechanical properties of aluminum alloy castings than the elongation or the tensile strength individual. It can be concluded that the Q value of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy reaches the maximum, which increases from 265.7 to 384.4, compared to the unmodified alloy, suggesting that La and Yb addition significantly improve the mechanical properties of Al-4.6Cu-1.6Mg alloy. Figure 9b compares the mechanical properties of Al-Cu-(Mg) alloys modified with different RE [32-36]. It can be noted that the Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy shows a excellent combination of strength and elongation than most other RE modified Al-Cu-(Mg) alloys as shown in Figure 9.

The fracture morphologies of Al-4.6Cu-1.6Mg alloys with different contents of La and Yb are characterized in Figure 10. It can be seen from Figure 10a that the fracture surface of the unmodified alloy reveals an evident brittle fracture, including numerous cleavage planes, which is in accordance with the low strength and strain of the unmodified alloy. With the increase of La and Yb addition, the number of cleavage planes decrease while the number of dimples increase, which changes the fracture behaviors of the alloys from brittle to ductile. When the La and Yb addition is 0.3 wt.%, the fracture surface of the alloy shows a ductile-brittle mixing fracture, containing some dimples and tearing ridges, as shown in Figure 10b. While the La and Yb addition reaches 0.6 wt.%, the fracture surface of the alloy mainly exhibits a ductile fracture, possessing the highest number of dimples (Figure 10c), which corresponds to the optimal strength and elongation. As the La and Yb addition further increases to 0.9 wt.%, the fracture surface of the alloy also belongs to a ductile-brittle mixing fracture, only including few dimples and tearing ridges (Figure 10d).

Grain refinement mechanisms

At present, the widely accepted refinement mechanisms for RE refining the grains of aluminum alloys mainly include heterogeneous nucleation and compositional undercooling theories.

Compared to the homogeneous nucleation, the heterogeneous nucleation can reduce the critical nucleation work of primary α-Al, thus refining the α-Al grain. Combining the results of SEM and TEM, it can be seen that adding La and Yb into Al-4.6Cu-1.6Mg alloy can form Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ particles. Hence, the refinement mechanism depends on the fact that the Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ particles can serve as the effective heterogeneous nucleation substrates for α-Al. The criterion for the nucleation substrate effectively promoting α-Al nucleation is that the disregistry between the substrate and the nucleated solid phase should be less than 12% [37]. Generally, the lattice disregistry between two phases is evaluated by Turnbull-Vonnegut equation. However, the equation imposes a strict constraint on the choice of a crystallographic relationship due to only considering planes of similar atomic arrangements. Thus, Bramfitt modified the Turnbull-Vonnegut equation in the light of angular difference between the crystallographic directions with the planes so that it could be applied to crystallographic combinations of two phases with planes of different lattice arrangements. The modified equation can be expressed as follows.

Where (hkl)_s is denoted as a low index plane of the substrate, (hkl)_n is denoted as a low index plane of the nucleated solid phase, [uvw]_s represents a low index direction in (hkl)_s, [uvw]_n represents a low index direction in (hkl)_n, d[uwn]_s denotes the atomic distance along [uvw]_s, d[uwn]_n denotes the atomic distance along [uvw]_n, θ is denoted as the angle between [uvw]_s and [uvw]_n. The α-Al phase has a face centered cubic crystal structure with the lattice constant a=b=c=0.4049 nm. Al₆Cu₆La has also a face centered cubic crystal structure with the lattice constat a=b=c=1.1899 nm. While Al_7.4Cu_9.6Yb₂ belongs to a trigonal system, with the lattice constant a=b=0.8691 nm, c=1.2698 nm and α=β=90°C, γ=120°C. For this study, the (220) of Al₆Cu₆La phase and the (110) of A_l7.4Cu_9.6Yb₂ phase are selected as the nucleating planes, respectively. Meanwhile, three low index planes (100), (110) and (111) of α-Al are selected as the matching planes. The crystallographic relationships between α-Al and Al₆Cu₆La, Al_7.4Cu_9.6Yb₂ used for planar disregistry calculations are depicted in Figure 11.

The parameters for the planar disregistry equation between α-Al and A_l6Cu₆La, A_l7.4Cu_9.6Yb₂ are presented in Tables 3 and 4, respectively.

Table 3. Parameters for the planar disregistry equation between α-Al and Al₆Cu₆La.

According to the results, the planar disregistry of (220)Al₆Cu₆La//(100)Al, (220)Al₆Cu₆La//(110)Al, (220)Al₆Cu₆La//(111)Al are 12.05%, 2.04% and 19.67, respectively. Meanwhile, the planar disregistry of (110)Al_7.4Cu_9.6Yb₂//(100)Al, (110)Al_7.4Cu_9.6Yb₂//(110)Al, (110)Al_7.4Cu_9.6Yb₂//(111)Al are 2.86%, 16.82% and 7.75%, respectively. The planar disregistry of (220)Al₆Cu₆La//(110)Al, (110)Al_7.4Cu_9.6Yb₂//(100)Al and (110)Al_7.4Cu_9.6Yb₂//(111)Al are less than 12%, indicating good orientation relationships between α-Al and Al₆Cu₆La, Al_7.4Cu_9.6Yb₂, which is consistent with the result of HRTEM image. Based on the crystallographic relationships, the Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ phases can be regarded as the effective heterogeneous nucleation substrates for α-Al, thus refining grains as shown in Tables 3 and 4.

Table 4. Parameters for the planar disregistry equation between α-Al and Al7.4Cu9.6Yb2.

According to Hume-Rothery theory, when the difference of atomic radius of two elements is more than 15%, it is difficult to form solid solution [38]. Table 5 presents the atomic radius and electronegativity of some alloying elements [39-41]. As can be seen, the atomic radius differences between La, Yb and Al are 30.8% and 35.7%, respectively. Therefore, the solubility of La and Yb atoms in the α-Al is very low, thus resulting in that La and Yb atoms enrich at solid-liquid interface front during the solidification process, which generates the local compositional undercooling as shown in Table 5.

Table 5. Atomic radius and electronegativity of the alloying elements.

Table 6. Calculated results of compositional undercooling criterion for different solute atoms.

The generation of compositional undercooling zone at the solid-liquid interface front can hinder the continuous growth of the α-Al grains, thus refining the α-Al grains. The criterion for generating compositional undercooling at the solid-liquid interface front can be given as follows [42].

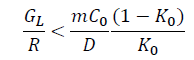
Where G_L devotes the temperature gradient of solid-liquid interface front, R is the advance speed of solid-liquid interface, m devotes the line slope of the liquid phase, C₀ is the initial composition concentration of the solute, K0 represents equilibrium distribution coefficient, D is diffusion coefficient.

Accordingly, the favorable conditions of compositional undercooling are low temperature gradient, fast solidification speed and high solute concentration of liquid phase for the given aluminum alloy. The influences of different solute atoms on the undercooling zone at the solid-liquid interface are evaluated. The parameters of compositional undercooling criterion for different solute atoms are presented in Table 6. Among them, the slope of the liquid us m and equilibrium distribution coefficient K0 of solute La and Yb can be obtained by the Al-La and Al-Yb binary phase diagrams [43]. The calculated results of compositional undercooling criterion for different solute atoms are shown in Table 6. According to the calculated results, it can be concluded that La and Yb atoms can obviously generate compositional undercooling during the solidification process, thus refining the grains as shown in Tables 6 and 7.

Table 7. Parameters of compositional undercooling criterion for different solute atoms [43-49].

Table 8. Parameters for the solute atoms and theoretical contributions to the yield strength from these solute atoms.

Interaction intensity

The interaction intensity between atoms can evaluate the effect of La and Yb addition on Al-4.6Cu-1.6Mg alloys, which reflects the stability of the alloy compounds and solid solubility. According to Darken-Gurry theory, the interaction intensity between solvent A and solute B may be calculated from the atomic radius and electronegativity (Table 5), which can be defined as [50].

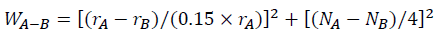
Where rA, rB and NA, NB are the atomic radius and electronegativity of solvent element A and solute element B, respectively. According to Equation, the interaction strength of Al-Cu and Al-Mg are 1.01 and 1.19, respectively. When RE elements are added into Al-4.6Cu-1.6Mg alloys, the interaction intensity can be expressed as.

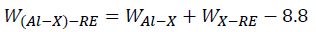
Based on Equation, the interaction strength of Al-Cu-La, Al-Cu-Yb, Al-Mg-La, and Al-Mg-Yb are 5.55, 6.59, -6.09 and -5.59, respectively. It is clearly that the addition of La and Yb can increase the interaction between Al and Cu, while decrease the interaction between Al and Mg. Therefore, adding La and Yb into Al-4.6Cu-1.6Mg alloys can promote the formation of new RE phases of Al₆Cu₆La and Al_7.4Cu_9.6Yb₂, and suppress the formation of Al2CuMg phase, which is consistent with the results of DSC curves.

Strength mechanisms

According to precious studies, the strengthening effect of La and Yb on the Al-4.6Cu-1.6Mg alloys should be mainly due to the refinement strengthening ΔσHP, solid solution strengthening ΔσSS and second phase strengthening ΔσSP [51-53]. Thus, the yield strength of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy can be estimated by the following equation.

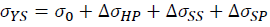
Where σ0 is the yield strength of the unmodified Al-4.6Cu-1.6Mg alloy and the value is 128.3 MPa. The grain refinement is attributed to comprehensive effect of heterogeneous nucleation and compositional undercooling. With the grain size decreases, the number of grain boundary increases, thus increasing the resistance to dislocation motion, which results in refinement strengthening. The refinement strengthening can be described by Hall-Petch equation.

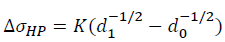
Where K is the grain boundary strengthening coefficient (150 MPa μm1/2), d1 and d0 are denoted as the average grain size of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy and Al-4.6Cu-1.6Mg alloy, respectively. Thus, the value of ΔσHP for the Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy is ~24.9 MPa.

In this study, solute elements Cu and Mg are easy to form solid solution with Al solvent. And, Cu and Mg are the first and second solute elements, respectively. Based on above analysis, adding La and Yb into Al-4.6Cu-1.6Mg alloy can suppress the formation of Al2CuMg, which leads to increasing the amount of solid solution of the alloying elements. Cu and Mg solute elements in the solid solutions result in lattice distortion, which increase the resistance to dislocation motion and makes it difficult to slip, thus increasing the strength of the alloys. The solid solution strengthening results from the interaction between solute atoms and dislocations, which can be expressed by the Fleischer equation [54].

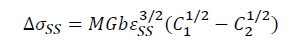
Where M is the Taylor factor (3.06), G is the shear modulus of the matrix (26.9 MPa for Al), b is the Burgers vector (0.286 nm), ε=(rx-rAl)/rAl is the lattice strain causing by the difference in atomic radius between the solute and solvent elements, C1 and C2 are the concentration of solute elements in the Al-4.6Cu-1.6Mg-0.6(La+Yb) and Al-4.6Cu-1.6Mg alloys, respectively. According to SEM statistical analysis results, C1 and C2 for solute Cu are 1.6 wt.% and 1.2 wt.%, respectively. And, C1 and C2 for solute Mg are 1.2 wt.% and 0.8 wt.%, respectively. Table 8 presents the parameters for the solute atoms and theoretical contributions to the yield strength from these solute atoms [54]. Thus, the increase in yield strength provided from solid solution strengthening is calculated to be ~12.9 MPa as shown in Table 8.

Some studies have indicated that the formation of Al-RE intermetallic could improve the mechanical properties of the aluminum alloys. These fine particles distributed in the matrix can hinder dislocations motion, thus increasing the strength of the alloys. This strengthening effect is known as the second phase strengthening. According to the interaction between the second phase and dislocations, the second phase strengthening mechanisms can be divided into Orowan cutting mechanism and Orowan bypassing mechanism. Generally, Orowan cutting mechanism works for the deformable particles (particles size less than 1 μm), while Orowan bypassing mechanism dominates for the non-deformable particles. As shown in Figure 6a, there are evident interactions between Al_7.4Cu_9.6Yb₂ particle and dislocations such as dislocation pile-up, indicating that Al_7.4Cu_9.6Yb₂ particle has strong structure stability. The Al_7.4Cu_9.6Yb₂ particle with 1.5 μm belongs to a non-deformable particle. Thus, Orowan bypassing mechanism can be used to calculate the contribution to yield strength from the second phase strengthening here, which can be expressed by [55].

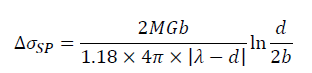
Where r represents the mean particle radius, λ represents particle interspacing and can be take to be the lattice distance in parallel planes [56]. Thus, the yield strength increment attributed to the second phase strengthening is estimated to be ~16.7 MPa for Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy.

According to equation, the theoretical yield strength of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy is ~182.8 MPa, which agrees well with the experimental value (181.2 MPa). Figure 12 displays the contribution ratios of different strengthening mechanisms to yield strength in Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy. It can be seen from Figure 12 that refinement strengthening is the main strengthening mechanism. This is because adding La and Yb into Al-4.6Cu-1.6Mg has evident grain refining effect, owing to synergistic effect of heterogeneous nucleation and compositional undercooling.

Conclusions

The combined effect of La and Yb on the microstructure and mechanical properties of Al-4.6Cu-1.6Mg alloys was investigated in this work. The main conclusions can be drawn as follows.

1. Adding La and Yb into Al-4.6Cu-1.6Mg alloy can form Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ phases, while suppress the formation of Al2CuMg phase at the same time.

2. Based on the calculated results of crystallographic relationships, the planar disregistry of (220)Al₆Cu₆La//(110)_Al, (110)Al_7.4Cu_9.6Yb₂//(100)_Al and (110)Al_7.4Cu_9.6Yb₂//(111)Al are less than 12%, indicating that Al₆Cu₆La and Al_7.4Cu_9.6Yb₂ can serve as the effective heterogeneous nucleation substrates for α-Al and thus refine grains.

3. According to the calculated results of compositional undercooling criterion for different solute atoms, La and Yb atoms can obviously generate compositional undercooling during the solidification process, thus refining grains.

4. The yield strength, ultimate tensile strength and elongation of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy are 181.2 MPa, 264.5 MPa and 6.3%, which are 41.2%, 45.1% and 75.0% higher than those of the unmodified alloy, respectively.

5. The strengthening mechanisms of Al-4.6Cu-1.6Mg-0.6 (La+Yb) alloy are attributed to the refinement strengthening, solid solution strengthening and second phase strengthening, in which the main strength mechanism comes from the refinement strengthening.

Acknowledgement

The authors express their gratitude to the National Natural Science Foundation of China (51965040) and Innovation Special Funds for Graduate Student of Jiangxi Province (YC2022-B018) for financial support.

Authorship Contributions

XLZ: Software, investigation, writing original draft, validation. LJY: Tensile Testing, investigation. ZJC: Investigation. HY: Conceptualization, review & editing, validation.

Data Availability

The data are available by the reasonable request.

Declarations

• Conflict of interest: The authors declare that they have no conflicts of interest in this work.

• Ethical approval: This study does not have ethical issues.

References

1. Bo GW, et al. Experimental and modeling investigations of the non-isothermal and isothermal precipitations in an Al-Cu-Mg-Zr alloy with various preprecipitation microstructures. Mater Des .2022;217:110640.

   [Crossref][Google Scholar]

2. Xu TY, et al. Enhancement of load transfer by interfacial bonding in Al-Cu-Mg joints under the in-situ synergistic effect of carbon nanotubes and silicon nitride. Mater Charact. 2022;191:112144.

   [Crossref][Google Scholar]

3. Sun TT, et al. Achieving excellent strength of the LPBF additively manufactured Al-Cu-Mg composite via in-situ mixing TiB2 and solution treatment. Mater Sci Eng A. 2022;850:143531.
4. Zhu C, et al. Hot-top direct chill casting assisted by a twin-cooling field: Improving the ingot quality of a large-size 2024 Al alloy. J Mater Sci Technol. 2022;112:114-122.

   [Crossref][Google Scholar]

5. Yue CY, et al. Effect of adding Pr on the microstructure and hot tearing sensitivity of as-cast Al-Cu-Mg alloys. Mater Charact. 2022;191:112141.

   [Crossref][Google Scholar]

6. Mei ZQ, et al. Effects of yttrium additions on microstructures and mechanical properties of cast Al-Cu-Mg-Ag alloys. J Alloy Compd. 2021;870:159435.

   [Crossref][Google Scholar]

7. Liang YH, et al. Influence of Er content on microstructural evolution and mechanical properties of Al-2Fe alloy. J Alloy Compd. 2022;895:162416.

   [Crossref][Google Scholar]

8. Yang X, et al. Effect of La on microstructure and corrosion behavior of 10%TiB2(p)/Al–5%Cu composites. J Mater Res Technol. 2020;9(4):7047-7058. [Crossref][Google Scholar]
9. Bai S, et al. Effects of small Er addition on the microstructural evolution and strength properties of an Al–Cu–Mg–Ag alloy aged at 200 °C. Mater Sci Eng A. 2019;766:138351.

   [Crossref][Google Scholar]

10. Du JD, et al.  Effect of Ce addition on the microstructure and properties of Al-Cu-Mn-Mg-Fe lithium battery shell alloy. Mater Charact. 2018,142:252-260.

    [Crossref][Google Scholar]

11. Li QL, et al. Effect of scandium addition on microstructure and mechanical properties of as-cast Al-5%Cu alloys. Vacuum. 2020;177:109385.

    [Crossref][Google Scholar]

12. Li JH, et al. Effect of combined addition of Zr, Ti and Y on microstructure and tensile properties of an Al-Zn-Mg-Cu alloy. Mater Des. 2022;223:111129.

    [Crossref][Google Scholar]

13. Amer SM, et al. Phase composition and mechanical properties of Al-Si based alloys with Yb or Gd addition. Mater Lett. 2022;320:132320.

    [Crossref][Google Scholar]

14. Zheng QJ, et al. Effect mechanisms of micro-alloying element La on microstructure and mechanical properties of hypoeutectic Al-Si alloys. J Mater Sci Technol. 2020;47:142-151.

    [Crossref][Google Scholar]

15. Jiang HX, et al. Effect of minor lanthanum on the microstructures, tensile and electrical properties of Al-Fe alloys. Mater Des. 2020;195:108991.

    [Crossref][Google Scholar]

16. Wang K, et al. Effects of trace ytterbium addition on the microstructure, mechanical and thermal properties of hypoeutectic Al-5Ni alloy. J Rare Earths. 2022;8:1305-1315.

    [Crossref][Google Scholar]

17. Xiong JJ, et al. Effects of Yb addition on the microstructure and mechanical properties of as-cast ADC12 Alloy. Metals. 2019;9:108.

    [Crossref][Google Scholar]

18. Shi ZP, et al. Microstructural evolution and strengthening mechanisms of a novel Al-11Si-3Cu alloy microalloyed with minor contents of Sr and Sc. Mater Sci Eng A. 2022;853:143738.

    [Crossref][Google Scholar]

19. Vijeesh V, et al. The effect of addition of Ce and Sr on the solidification path of Al-8Si-2Cu Alloy. Trans Indian Inst Met. 2015;68(6):1119-1123.

    [Crossref][Google Scholar]

20. Zou YC, et  al. Effect of rare earth Yb on microstructure and corrosion resistance of ADC12 aluminum alloy. Intermetallics. 2019;110:106487.

    [Crossref][Google Scholar]  

21. Qiu CR, et al. Synergistic effect of Sr and La on the microstructure and mechanical properties of A356.2 alloy. Mater Des. 2017;114:563-571.

    [Crossref][Google Scholar] 

22. Wang TM, et al. Combining effects of TiB2 and La on the aging behavior of A356 alloy. Mater Sci Eng A. 2015;644:425-430.

    [Crossref][Google Scholar] 

23. Chen ZW, et al. Microstructures and mechanical properties of Al-Cu-Mn alloy with La and Sm addition. Rare Met. 2012;31(4):332-335.

    [Crossref][Google Scholar] 

24. Zhang XM, et al. Effects of Yb addition on microstructures and mechanical properties of 2519A aluminum alloy plate. Trans Nonferrous Met Soc China. 2010;20:727-731.

    [Crossref][Google Scholar] 

25. Yao DM, et al. Effects of La on the age hardening behavior and precipitation kinetics in the cast Al-Cu alloy. J Alloy Compd. 2012;540:154-158.

    [Crossref][Google Scholar]

26. Huang G, et al. Thermodynamic description of the Al-Cu-Yb ternary system supported by first-principles calculations. J Min Metall Sect B. 2016;52:177-183.

    [Crossref][Google Scholar]

27. Zou XL, et al. Thermodynamic and kinetic analysis of ternary intermetallics formation in Al-Cu-La alloy. Phys B. 2022;646:414254.

    [Crossref][Google Scholar]  

28. Qiu MK, et al. Synergistic effects of the combined addition of (Ce+Yb) on the microstructure and mechanical properties of Al-Si-Mg-Cu-Cr casting alloy. Int J Metalcast. 2021;16:1206-1220.

    [Crossref][Google Scholar] 

29. Hu Z, et al. Solidification behavior, microstructure and silicon twinning of Al-10Si alloys with ytterbium addition. J Rare Earths. 2018;36:662-668.

    [Crossref][Google Scholar] 

30. Li JH, et al. Nucleation kinetics of entrained eutectic Si in Al-5Si alloys. Acta Mater. 2014;72:80-98.

    [Crossref][Google Scholar] 

31. Tang Q, et al. The effects of neodymium addition on the intermetallic microstructure and mechanical properties of Al-7Si-0.3Mg-0.3Fe alloys. J Alloy Compd. 2018;741:161-173.

    [Crossref][Google Scholar] 

32. Xu GF, et al. Microstructure and properties of Al-4Cu alloy containing Sc. Trans Nonferrous Met Soc. 2004;14:63-66.

    [Crossref][Google Scholar] 

33. Song ZX, et al. Effect of La and Sc co-addition on the mechanical properties and thermal conductivity of as-cast Al-4.8% Cu alloys. Metals. 2021;11:1866.

    [Crossref][Google Scholar] 

34. Qin J, et al. Study on the formation and regulation mechanism of W phase and the improvement of mechanical properties in homogenization of cast Al-Cu-Sc-Zr alloys: Experiments and calculations. Vacuum. 2023;207:111631.

    [Crossref][Google Scholar] 

35. Chen Y, et al. Microstructure characterization and mechanical properties of crack-free Al-Cu-Mg-Y alloy fabricated by laser powder bed fusion. Addit Manuf. 2022;58:103006.

    [Crossref][Google Scholar] 

36. Tao CC, et al. Effect of La on hot cracking susceptibility of Al-Cu-Mg alloy. Mater Res Express. 2019;6:105802.

    [Crossref][Google Scholar] 

37. Bramfitt BL. The effect of carbide and nitride additions on the heterogeneous nucleation behavior of liquid iron. Metall Trans. 1970;1:1987-1995.

    [Crossref][Google Scholar] 

38. Zhang YM, et al. Revisiting Hume-Rothery’s rules with artificial neural networks. Acta Mater 2008;56:1094-1105.

    [Crossref][Google Scholar] 

39. Du JD, et al.  Effect of CeLa addition on the microstructures and mechanical properties of Al-Cu-Mn-Mg-Fe alloy. Mater Charact. 2017;123:42-50.

    [Crossref][Google Scholar]   

40. Xie HB, et al. Atomic-scale HAADF-STEM characterization of an age-hardenable Mg-Cd-Yb alloy. J Alloy Compd. 2019;770:742-747.

    [Crossref][Google Scholar] 

41. Jia L, et al. Preparation and thermophysical properties of RE2CrTaO7 (Y, Sm, Dy, Yb) ceramics for thermal barrier coating applications. Ceram Int. 2022;48:23814-23820.

    [Crossref][Google Scholar]   

42. Song XC, et al. Impact of rare earth element La on microstructure and hot crack resistance of ADC12 alloy. J Wuhan Univ Technol. 2018;33:193-197.

    [Crossref][Google Scholar] 

43. Baker H, et al. ASM Handbook Volume 03 : Alloy Phase Diagrams, ASM International. Materials Park.1998;303-334.
44. Ezemenaka D, et al. Microstructural evolution in directionally solidified Al-Cu-Mg ternary eutectic. J Alloy Compd. 2021;883:160818.

    [Crossref][Google Scholar]   

45. Easton MA, et al. Grain refinement of aluminum alloys: Part I. the nucleant and solute paradigms-a review of the literature. Metall Mater Trans A. 1999; 30:1613-1623.

    [Crossref][Google Scholar]

46. Ji DB, et al. Liquid Al assisted electrochemical extraction of lanthanum by formation of Al11La3 in chloride melts. J Nucl Mater. 2020; 542:152477.

    [Crossref][Google Scholar]

47. Knipling KE, et al. Criteria for developing castable, creep-resistant aluminum-based alloys-A review. Z Metallkd. 2006; 97:246-265.

    [Crossref][Google Scholar]

48. Ceresara S.  A step annealing procedure for the determination of diffusion coefficients in metals by the resistometric method-application to the diffusion of Cu in Al. Phys Stat Sol. 1968; 27:517-520.

    [Crossref][Google Scholar]

49. Du Y, et al.  Diffusion coefficients of some solutes in fcc and liquid Al: critical evaluation and correlation. Mater Sci Eng A. 2003; 363:140-151,

    [Crossref][Google Scholar]

50. Bai ZH, et al. Design of a in-situ crystallization inoculant of Al-Cu alloys by addition of lanthanum. J Mater Res Technol. 2022; 18:852-858.

    [Crossref][Google Scholar]

51. Qin J, et al. The effect of sc addition on microstructure and mechanical properties of as-cast Zr-containing Al-Cu alloys. J Alloy Compd. 2022; 909:164686.

    [Crossref][Google Scholar]

52. Kendig KL, et al.  Strengthening mechanisms of an Al-Mg-Sc-Zr alloy. Acta Mater. 2002; 50:4165-4175.

    [Crossref][Google Scholar]

53. Zhang MS, et al. Quantifying the effects of Sc and Ag on the microstructure and mechanical properties of Al–Cu alloys. Mater Sci Eng A. 2022; 831:142355.

    [Crossref][Google Scholar]

54. Ma KK, et al.  Mechanical behavior and strengthening mechanisms in ultrafine grain precipitation-strengthened aluminum alloy. Acta Mater. 2014; 62:141-155.

    [Crossref][Google Scholar]

55. Cao FR, et al. Mechanical properties and microstructural evolution in a superlight Mg-7.28Li-2.19Al-0.091Y alloy fabricated by rolling. J Alloy Compd. 2018; 745:436-445.

    [Crossref][Google Scholar]

56. Li RD, et al. Developing a high-strength Al-Mg-Si-Sc-Zr alloy for selective laser melting: Crack-inhibiting and multiple strengthening mechanisms. Acta Mater. 2020; 193:83-98.

    [Crossref][Google Scholar]